回溯模板——子集型回溯【含python源码】
文章目录
- 前言
- 一、子集型回溯:
- 二、模板:
-
-
-
- 子集型回溯模板一:
- 子集型回溯模板二:
-
-
- 三、leetcode上相关的例题:
-
-
-
- 1、[子集](https://leetcode.cn/problems/subsets/)
- 2、[括号生成](https://leetcode.cn/problems/generate-parentheses/)
- 3、[电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)
- 4、[分割回文串](https://leetcode.cn/problems/palindrome-partitioning/)
-
-
前言
看了一个大佬灵山茶艾府在B站讲解回溯的视频后,我悟了。太强了吧,我觉得很有必要来一个学习记录。灵神视频链接
一、子集型回溯:
构造长为 n 的字符串(原问题) -> 枚举一个字母 -> 构造长为 n - 1 的字符串(子问题)
可以发现子问题和原问题是相似的,这种由原问题到子问题的过程适合用递归解决。
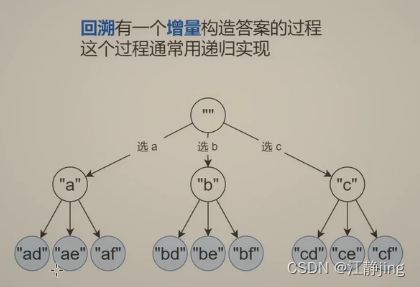
注意:
1、写清楚边界条件和非边界条件
2、递归参数中的 i 不只是第 i 个,而是 >= i 的这部分
二、模板:
子集型回溯模板一:
def f1(nums):
# 先得到列表长度 n(判断 n <= 0 的情况,选择直接返回[]或者其他)
n = len(nums)
# 设置一个列表 ans 用于存储所有的结果
ans = []
# 设置一个列表 path 用于存储当前递归得到的单个结果
# path 可能是定长的,也可能是不定长的(这里是是不定长的)
path = []
# 接着写 dfs 函数
def dfs(i):
if i == n: # 判断是边界条件
ans.append(path.copy()) # 将当前得到的结果 path 放入 总结果 ans 中
return # 直接 return 后,代表当前层次的 dfs 运行结束
# 以下为非边界条件
# (1)不选,直接进入下一层次的 dfs
dfs(i + 1)
# (2)选,再下一步
path.append(nums[i])
dfs(i + 1) # 进入下一层次的 dfs
path.pop() # 在列表中添加数据的要删除掉,而直接设置 path[i] 值的不用
# 从第 0 层开始进入 dfs
dfs(0)
return ans
子集型回溯模板二:
def f2(nums):
n = len(nums)
ans = []
path = []
def dfs(i):
# 开始就将当前单个结果 path 放入总结果 ans 中
ans.append(path.copy()) # path 是数组(可变)不是字符串(不可变),需要 copy,或者使用path[:]
if i == n: # 判断边界条件
return
for j in range(i, n): # 若为非边界条件,从当前位置遍历到结束位置
path.append(nums[j]) # 测试每一个
dfs(j + 1) # 进入下一层次
path.pop() # 回溯,将前面改变的数据(添加了一个数),再变回去(再减掉一个数)
dfs(0)
return ans
三、leetcode上相关的例题:
1、子集
"""
子集回溯的两种代码模板:
"""
def f1(nums):
# 先得到列表长度 n(判断 n <= 0 的情况,选择直接返回[]或者其他)
n = len(nums)
# 设置一个列表 ans 用于存储所有的结果
ans = []
# 设置一个列表 path 用于存储当前递归得到的单个结果
# path 可能是定长的,也可能是不定长的(这里是是不定长的)
path = []
# 接着写 dfs 函数
def dfs(i):
if i == n: # 判断是边界条件
ans.append(path.copy()) # 将当前得到的结果 path 放入 总结果 ans 中
return # 直接 return 后,代表当前层次的 dfs 运行结束
# 以下为非边界条件
# (1)不选,直接进入下一层次的 dfs
dfs(i + 1)
# (2)选,再下一步
path.append(nums[i])
dfs(i + 1) # 进入下一层次的 dfs
path.pop() # 在列表中添加数据的要删除掉,而直接设置 path[i] 值的不用
# 从第 0 层开始进入 dfs
dfs(0)
return ans
def f2(nums):
n = len(nums)
ans = []
path = []
def dfs(i):
# 开始就将当前单个结果 path 放入总结果 ans 中
ans.append(path.copy()) # path 是数组(可变)不是字符串(不可变),需要 copy,或者使用path[:]
if i == n: # 判断边界条件
return
for j in range(i, n): # 若为非边界条件,从当前位置遍历到结束位置
path.append(nums[j]) # 测试每一个
dfs(j + 1) # 进入下一层次
path.pop() # 回溯,将前面改变的数据(添加了一个数),再变回去(再减掉一个数)
dfs(0)
return ans
nums = [1, 2, 3]
ans = f2(nums)
print(ans)
2、括号生成
def generateParenthesis(n):
if n <= 0:
return []
res = []
def dfs(paths, left, right):
if left > n or right > left: # 该树枝结束(剪枝)
return
if len(paths) == n * 2: # 结束条件
res.append(paths)
return
dfs(paths + '(', left + 1, right)
dfs(paths + ')', left, right + 1)
dfs('', 0, 0) # 起始状态
return res
def f(n):
m = 2 * n
path = [''] * m # path 是不定长的
ans = []
def dfs(i, left):
if i == m:
ans.append(''.join(path))
return
if left < n:
path[i] = '('
dfs(i + 1, left + 1)
if (i - left) < left:
path[i] = ')'
dfs(i + 1, left)
dfs(0, 0)
return ans
# n = int(input())
# print(generateParenthesis(n))
n = 3
print(f(n))
3、电话号码的字母组合
def f(digits):
MAPPING = ["", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"]
n = len(digits)
if n == 0:
return []
ans = [] # 存放总体结果
path = [''] * n # 存放一个结果字符串(path 是不定长的)
def dfs(i):
if i == n:
ans.append(''.join(path))
return
for c in MAPPING[int(digits[i])]:
path[i] = c # i 位置放大字符
dfs(i + 1)
dfs(0)
return ans
dight = "23"
res = f(dight)
print(res)
4、分割回文串
def f(s):
n = len(s)
ans = []
path = []
def dfs(i):
if i == n:
ans.append(path.copy())
return
for j in range(i, n):
t = s[i: j + 1]
if t[::-1] == t:
path.append(t)
dfs(j + 1)
path.pop()
dfs(0)
return ans
s = "aab"
ans = f(s)
print(ans)
如有侵权,可联系删除,共勉。