特征工程—PCA与SVD降维基础

对于一张表，维度可以是样本数量，也可以是特征数量，一般情况是特征数量

特征矩阵：特指二维数据，只有行列，构成表，通常是dataframe

降维：降低特征矩阵的特征数量，可以将高维数据转化为三维以下数据进行可视化，并且加快算法的运行。

sklearn中使用decomposition模块进行降维操作。

主成分分析 = 降维 = PCA,SVD：降维后包含特征的主成分，无用特征可能是噪音。

sklearn中有两种降维方式：PCA与SVD

PCA：方差是信息衡量指标，样本方差越大，包含信息量越大（方差是对于单个特征而言）

SVD：奇异值是信息衡量指标，原理与PCA基本一致

PCA与SVD可以单独实现降维。

 矩阵分解：降维后的整个数据的方差和不变，特征变少，但信息量损失较少。

特征选择：不同于降维，特征选择在数据中直接选择特征数据。

重要参数：n_components:降维后的维度，（维度不能高于特征数量的最小维度）

降维数据可视化：只有降维到三维以下才可可视化

使用iris数据进行降维操作

#高维数据可视化案列
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA

iris = load_iris() #实列化
y = iris.target    #标签
x=  iris.data       
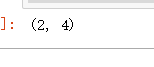
x.shape           #查看维度，是二维数据

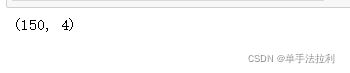
 （表示150行，4列数据，二维表，表中是思维数据）

import pandas as pd
pd.DataFrame(x)    #查看特征矩阵维度，是四维特征矩阵，四个特征

 将iris数据降到二维进行可视化

p = PCA(n_components=2)   #实列化
re = p.fit_transform(x)   #训练
re

 使用布尔索引找出原数据中的不同的类

y==0  #找出原数据中的第0类数据

 上述数据中，true表示原数据中的第0类，在降维后的数据定位第0类

降维到二维，会出现两个array数组

re[y==0,0],re[y==0,1]  #对降维后的数据，从第0列与第一列取出y==0的值

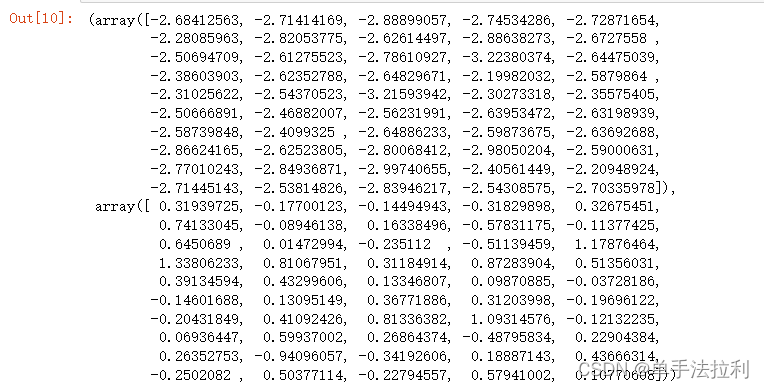
 将降维后的数据可视化

plt.figure()
plt.scatter(re[y==0,0],re[y==0,1],c = "red",label = iris.target_names[0])
plt.scatter(re[y==1,0],re[y==1,1],c = "blue",label = iris.target_names[1])
plt.scatter(re[y==2,0],re[y==2,1],c = "black",label = iris.target_names[2])
plt.legend()
plt.show()

 降维后数据的信息量会变少

p.explained_variance_  #查看数据所带的信息量大小

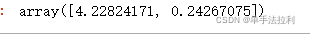
p.explained_variance_ratio_  #表示特征信息量的百分比，又叫可解释方差贡献率

 

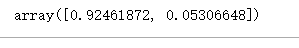
 将降维后的方差贡献率进行求和，就是降维后数据的总信息量

p.explained_variance_ratio_.sum()

 使用最大似然估计法（mle）让PCA模型自动找出降维后的最佳信息量

p_mle = PCA(n_components="mle")  #mle表示最大似然估计方法
re = p_mle.fit_transform(x)
re

p_mle.explained_variance_ratio_.sum()   #查看降维后的数据包含的信息量百分比

 可以指定降维后数据包含的信息量进行降维操作

p = PCA(n_components=0.97,svd_solver="full")  #实列化，使用n_components选取指定百分比的信息量进行降维，需要加上“full”语句
re = p.fit_transform(x)
re

 PCA与SVD都是矩阵分解方法，但是SVD相比于PCA更快

PCA(2).fit(x).components_  #查看SVD分解后矩阵  PCA（2）表示降维第二种方法SVD

PCA(2).fit(x).components_.shape   #SVD降维后的新特征空间 V（K，N）

 

 SVD重要参数svd_solver与random_state,其中svd_solver用于控制矩阵分解模式，具有“auto”，“full”，“arpack”，“randomized”四种模式，通常情况下使用auto模式，并且只有在“arpack”与“randomizad”模式下才可以使用random_state。