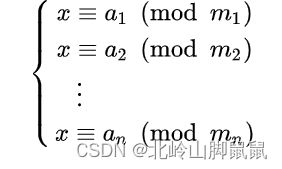中国剩余定理模板与证明+扩展（两种不同线性同余方程组的解法）

中国剩余定理： 

 给出如上的一组一元线性同余方程组，ai是任意整数，mi则是两两互质的整数，要求一个x满足方程组。

解法：

1. 设一个m是所有mi累乘的积，设一个M数组使得M[i]==m/mi.

2.设ti是线性同余方程 M[i] * ti ≡ 1（mod mi）的一个解,  相当于求M[i]在mod（mi）下的逆元

3.由第2点以及模运算的性质可以结合上图推出以下公式 

   xi = ai * M[i] * ti  ≡ ai （mod mi）  因为模数之间两两互质，所以可以推出这条公式一定成立

4. 由以上3点可以推出一个合法答案x= （x1+x2+x3+...）

     证明： 结合上图

                 在x ≡ a1 （mod m1）当中，真正起作用使得余数为a1的部分只有x1，那其他的xi的都                   在干嘛呢？

                 以x2为例，x2的组成是ai * M[2] * ti ，在这之中M[2]是 m/m2,所以M[2]是m1的倍数，因                  此x2%m1的结果是0，x3~xn也是同理。

5.最后得出来的x就是一个合法解，如果题目要求最小的            非负整数解则可以让x对m取模让x落在        [0,m-1]的范围内。

代码：

ll china(ll m[] ,ll a[] ,int n) //a数组是余数数组，m数组是除数数组
{
    ll M=1,y,x=0;
    for( int i=1;i<=n;i++) //累乘得到 m
        M*=m[i];
    for(int i=1;i<=n;i++)
    {
        ll w=M/m[i];
        ll tx=0;
        exgcd(w,m[i],tx,y);
        x=(x+w*tx*a[i])%M;  //这里就是在累加每一个xi
    }
    return (x+M)%M; //使得x落在0~m-1的范围
}

题目传送门：中国剩余定理

思路：上面

完整代码：

#include
#include
#include
#include

扩展内容：

题目：204. 表达整数的奇怪方式 - AcWing题库

在上面的题目当中，如果模数之间并不满足两两互质的要求就不能使用中国剩余定理去解题了。

在此情况需要新的算法来。

1.首先从最小的两个方程组的情况来看，设有：

x≡m1(mod a1)   ==     x=k1*a1+m1

x≡m2(mod a2)   ==    x=k2*a2+m2

由上面的两条式子可以得到 

k1*a1+m1==k2*a2+m2  进而得到  k1*a1-k2*a2==m2-m1 

由贝祖定理得知上面的式子成立的条件是gcd(a1,a2) | m2-m1 设d为gcd（a1,a2）

2.由上面的式子又可以等价变换的得到

(k1+k*a2/d)*a1 - (k2+k*a1/d)*a2==m2-m1

到这里我们就可以获得这两条式子的一个通解：

x=k1*a1+m1==(k1+k*a2/d)*a1 +m1  在这里面，k是任意整数

而上面的式子中k1已经是一个可以通过一次扩展欧几里得算法得到的已知量。

再将上面的式子进行变形得到

x= (  a1*k1 + m1) +k*(a1*a2)/d 

这条式子就形如一条新的同余方程  x= k * a  +  m,这条式子就是两条同余方程合并后得到的一条新的同余方程。

只要进行n-1次合并就能得到答案。

注意点：

题目的数据范围较小是因为题目中有一个模数相乘的步骤，容易发生溢出，

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=30;
ll a[N],m[N];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(!b) {x=1,y=0;return a;}
    ll  d=exgcd(b,a%b,x,y);
    ll t=x;
    x=y;
    y=t-y*(a/b);
    return d;
}
int main()
{
    int n;
    cin>>n;
    bool flag=true;
    ll a1,m1;
    cin>>a1>>m1;
    for(int i=1;i>a2>>m2;
          ll k1,k2;
          ll d=exgcd(a1,a2,k1,k2);
        if((m2-m1)%d) //不满足条件直接就无解了
        {
            flag=false;
            break;
        }
        k1*=(m2-m1)/d;
        ll t=a2/d;
        k1=(k1%t+t)%t;//为防溢出要使k1变成最小的正整数解

        m1=a1*k1+m1;
        a1=abs(a1/d*a2);//正负都可
    }
    if(flag)
        cout<<(m1%a1+a1)%a1; //输出最小的正整数解
        else
        cout<<-1<