牛客竞赛:2023牛客寒假算法基础集训营1
目录
C现在是,学术时间 (I)
题目分析:
D现在是,学术时间 (II)
题目分析:
E 鸡算几何
知识点:
F鸡玩炸蛋人
题目分析:
G鸡格线
知识点:
线段树:
题目分析:
K本题主要考察了dp
题目分析:
L本题主要考察了运气
知识点:
题目分析:
M本题主要考察了找规律
题目分析:
C现在是,学术时间 (I)
登录—专业IT笔试面试备考平台_牛客网
题目分析:
不进行重新分配的话是最优的
题目中明确指出:
该教授发表的所有论文中,有至少H篇论文的引用量大于等于H
每篇论文有一个引用量,这个引用量是固定的,故等于0的就不能选择,相当于这篇文章应该被舍
)
故只要这篇论文的引用量不为0就可以给每位教授一人分布一篇文章(实际上只要统计引用量非0的论文篇数即可,而每位教授又只有一篇故只要引用量非0即可发布因为非0的引用量一定>=1。
#include
using namespace std;
const int N=1e6+10;
int t,n,a[N],ans;
int main()
{
cin>>t;
while(t--)
{
ans=0;
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>a[i];
ans++;
}
cout< D现在是,学术时间 (II)
登录—专业IT笔试面试备考平台_牛客网
题目分析:
题目所求就是其(交集/并集)的最大值
#include
using namespace std;
int t,x,y,xp,yp;
double s1,s2,ans,h;
int main()
{
cin>>t;
while(t--)
{
cin>>x>>y>>xp>>yp;
if(xp<=x&&yp<=y)
{
s1=max(xp,x-xp)*max(yp,y-yp);
s2=x*y;
ans=s1*1.0/s2;
}
else if(xp<=x&&yp>=y)
{
h=max(xp,x-xp);
s1=h*y;
s2=x*y-s1+yp*h;
ans=s1*1.0/s2;
}
else if(xp>=x&&yp<=y)
{
h=max(yp,y-yp);
s1=h*x;
s2=x*y-s1+xp*h;
ans=s1*1.0/s2;
}
else if(xp>=x&&yp>=y)
{
s1=x*y;
s2=xp*yp;
ans=s1*1.0/s2;
}
printf("%0.9lf\n",ans);
}
return 0;
} E 鸡算几何
登录—专业IT笔试面试备考平台_牛客网
知识点:
注:精度问题
考虑比较AB和BC长度时使用整数而非浮点数比较,或在ABC和DEF进行匹配时使用较大的
eps(如1e-5,注意这里使用较小的如1e-9等eps反而可能爆炸)(很可能本来相等的一组线段因为定义过于严格从而变得不相等)
F鸡玩炸蛋人
登录—专业IT笔试面试备考平台_牛客网
题目分析:
分类讨论一下:
1.如果没有任何一个连通块内有蛋
那么说明任意起点终点都可以满足要求因为只要移动不用下蛋
2.如果只一个连通块中有蛋那么说明我的起点和终点得放在这个连通块内所以任意挑这个连通块的两个点就行
3.如果有超过一个连通块中有蛋因为各个连通块是不互相连通的那么必然不可能从一个连通块走到另一个连通块也就是不可能跨连通块下蛋也就是说此方案无解
只要有蛋就说明经过了
#include
using namespace std;
const int N=1e5+10;
long long n,m,id,ans,u,v,a[N],p[N],cnt[N];
int find(int x)
{
if(x!=p[x])p[x]=find(p[x]);
return p[x];
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
p[i]=i;
}
while(m--)
{
cin>>u>>v;
p[find(u)]=find(v);
}
int id=0;
for(int i=1;i<=n;i++)
{
cin>>a[i];
if(a[i])//判是不是蛋存在于两个连通块内
{ //id表示第一次遍历到蛋的时候蛋所在的连通块
if(id&&id!=find(i))//如果这次遍历到蛋发现不在这个连通块内了
{ //说明这个有两个连通块有蛋
cout<<0; //就是第三种情况
return 0; //输出0
}
id=find(i);
}
cnt[find(i)]++;
}
for(int i=1;i<=n;i++)
{
if(id==0||i==id)//i==id简单理解为i==find(i),id==0就是没有任何连通块有蛋的情况,没有蛋的时候每个根节点都要统计
ans+=cnt[i]*cnt[i];//有蛋就统计那一个根节点
}
cout< G鸡格线
登录—专业IT笔试面试备考平台_牛客网
知识点:
线段树:
概念:
线段树是一种二叉树,广义上也被归类为二叉搜索树,对于区间的维护修改和查询时间复杂度优化为log级别
具体操作:
对于一个区间我们让它平均的划分为两个区间,两个区间又各自划分为两个区间,直达划分到仅有一个数据的区间,每个区间存放一个或多个我们需要的数据,比如可以表示区间的和或者是这个区间的最大或最小值,我们用树的形式来存放这些数据便构成了一棵二叉树,而这种存放区间数据的二叉树我们称之为线段树
线段树的维护:
小区间更新大区间(线段树是平衡二叉树)
线段树使用的局限性:
问题需要满足:区间加法(因为这样才能将大问题化为子问题解决)
区间加法:对于[L,R]的区间,它的答案可以由[L,M]和[M+1,R]的答案合并求出(M为区间中点)
满足的问题:区间求和,区间最大最小值等
不满足的问题:区间的众数,区间最长连续问题,最长不下降问题等
线段树解决问题的步骤:
1.建树
2.单点修改/区间修改(区间修改后的查询会用到
3.区间查询
建树:
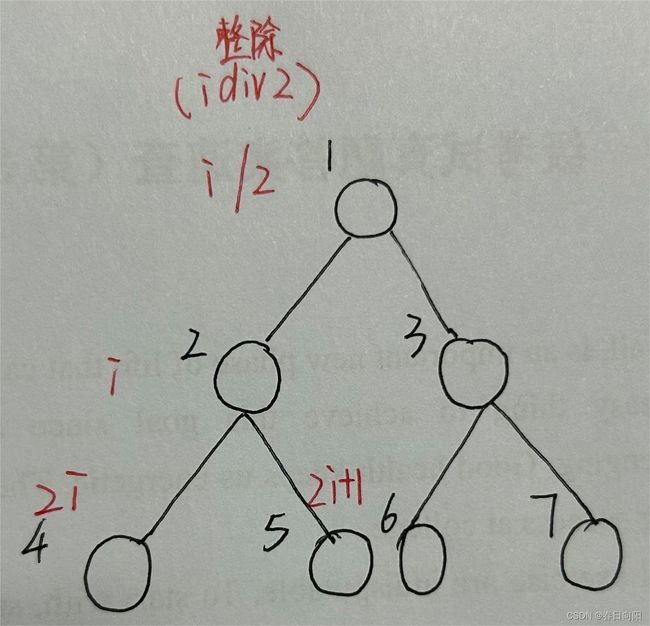
以堆的方式存储数据
注意:
线段树的数组要开到4*n
单点修改:
修改数列中下标为i的数据,从根节点向下深搜
如果当前节点的左儿子的区间[L,R]包含了i,也就是L<=i<=R,就访问左儿子,否则就访问右儿子,直到L=R也就是只包含这个数据的节点就可以修改它,不要忘了将包含此数据的大区间的值更新
如果要查询的区间完全覆盖当前区间直接返回当前区间的值
如果查询区间和左儿子有交集搜索左儿子
如果查询区间和右儿子有交集搜索右儿子
最后合并处理两边查询的数据
区间修改:
如果按照常规思路乡下递归遍历所有节点一一修改时间复杂度和暴力处理相差无几
此时可以用到lazy标记:
将此区间标记,表示这个 区间的值已经更新,但它的子区间却没有更新,更新的信息就是标记里存的值
区间修改步骤:
如果要修改的区间完全覆盖当前区间直接更新这个区间,打上lazy标记
如果没有完全覆盖,且当前区间有lazy标记,先下传lazy标记到子区间,再清楚当前区间的lazy标记
如果修改区间和左儿子有交集搜索左儿子
如果修改区间和右儿子有交集搜素右儿子
最后将当前区间的值更新
区间修改后的区间查询:
如果要查询的区间完全覆盖当前区间,直接返回当前区间的值
如果没有被完全包含,下穿lazy标记
如果查询区间和左儿子有交集,搜索左儿子
如果查询区间和右儿子有交集,搜索右儿子
最后合并处理两边查询的数据
代码模板:
注:对于修改一个数之类的操作一般不需要lazy 标记,一般lazy标记用于整个区间
u表示每个数的编号,mid为区间端点值
定义线段树中的结构体:
struct node { int l,r; int v; //区间[l,r]中的最大值 }tr[N*4]; //注意要开[N*4]的区间范围建立线段树:
void build(int u,int l,int r)//u:当前节点的编号 L:当前区间的左端点 r:当前区间的右端点 { tr[u]={l,r}; //当前节点的左右儿子分别为l和r if(l==r)return;//如果是叶节点直接return int mid=l+r>>1;//不是叶节点求一下当前区间的中点是多少 build(u<<1,l,mid),build((u<<1)+1,mid+1,r);//递归建立左右区间(左儿子所在区间u*2, } //右儿子所在区间为u*2+1由子节点的信息来计算父节点的信息:(用于回溯时的更新)
void pushup(int u) { tr[u].v=max(tr[u<<1].v,tr[(u<<1)+1].v);//父节点的最大值为左右儿子的最大值取一个max }查询操作:(此处为查询区间中的v)
int query(int u,int l,int r)//u:表示当前线段树的端点 l,r:表示我们查询的区间 { if(tr[u].l>=l&&tr[u].r<=r)return tr[u].v;//树中节点,已经被完全包含在[l,r]中了 int mid=tr[u].l+tr[u].r>>1; int v=0; if(l<=mid)v=query(u<<1,l,r); //如果和左边有交集 if(r>mid)v=max(v,query((u<<1)+1,l,r));//如果和右边有交集 return v; }查询区间的最大子段和:
此时定义的结构体为:
struct node { int l,r; int tmax; //最大连续子段和 int lmax; //最大前缀和 int rmax; //最大后缀和 int sum; //区间和 }tr[N*4];横跨左右子区间的最大子段和=max
(左儿子的最大字段和,右儿子的最大字段和,左子区间的最大后缀+右子区间的最大前缀)
void pushup(node &u,node &l,node &r) { u.sum=l.sum+r.sum; u.lmax=max(l.lmax,l.sum+r.lmax); u.rmax=max(r.rmax,r.sum+l.rmax); u.tmax=max(max(l.tmax,r.tmax),l.rmax+r.lamx); }修改操作:
void modify(int u,int x,int v) { if(tr[u].l==x&&tr[u].r==x)tr[u].v=v;//找到叶节点直接修改即可 else //说明当前节点不是叶节点,判断往左右哪边递归 { int mid=tr[u].l+tr[u].r>>1; if(x<=mid)modify(u<<1,x,v); else modify((u<<1)+1,x,v); pushup(u);//此处为回溯是更新父节点,因为上方进行了更新子节点的操作 } }下方lazy标记!!!
区间:
核心5函数:
1.pushup
2.pushdown
3.build
4.modify
5.query
结构体:
struct node { int l,r; LL sum,lazy; }tr[4*N];由子节点的信息来计算父节点的信息:(由下至上对应pushdown用于回溯时的更新)
void pushup(int u) { tr[u].sum=tr[u<<1].sum+tr[(u<<1)+1].sum; }下传lazy标记pushdown:(由下至上对应pushup)
void pushdown(int u) { auto &root=tr[u],&left=tr[u<<1],&right=tr[(u<<1)+1]; if(root.lazy) { //下传lazy标记,更新子树 left.lazy+=root.lazy,left.sum+=(LL)(left.r-lrft.l+1)*root.lazy; right.lazy+=root.lazy,right.sum+=(LL)(right.r-right.l+1)*root.lazy; //删除父节点lazy标记 root.lazy=0; } }建立线段树:
void build(int u,int l,int r) { if(l==r)tr[u]={l,r,a[l],0}; else { tr[u]={l,r}; int mid=l+r>>1; build(u<<1,l,mid),build((u<<1)+1,mid+1,r); pushup(u); } }修改区间:
void modify(int u,int l,int r,int v) { if(l<=tr[u].l&&tr[u].r<=r) { tr[u].sum+=(tr[u].r-tr[u].l+1)*v; tr[u].lazy+=v; } else { pushdown(u);//下传lazy标记 in mid=tr[u].l+tr[u].r>>1; if(l<=mid)modify(u<<1,l,r,v);//修改 if(r>mid)modify((u<<1)+1,l,r,v); pushup(u);//通过子区间的修改更新父节点 } }查询区间:
LL query(int u,int l,int r) { if(l<=tr[u].l&&tr[u].r<=r)return tr[u].sum; pushdown(u); int mid=tr[u].l+tr[u].r>>1; LL v=0; if(l<=mid)v=query(u<<1,l,r); if(r>mid)v+=query((u<<1)+1,l,r); return v; }
题目分析:
注意此题:不用lazy标记!!!维护的是区间的最值
当a[i]=0,99,100时经过操作它们的值不会发生变化
所以维护最小值大于99 最大值小于100就行
对于初始的0(其他数不会变为0)可直接让最值为99或100(不影响)
#include
using namespace std;
typedef long long LL;
const int N=1e5+10;
int a[N],n,m,op,l,r,k;
struct node
{
int l,r;
LL sum;
int maxx,minn;
}tr[4*N];
int f(int x)
{
return round(10*sqrt(x));
}
void pushup(int u)
{
tr[u].minn=min(tr[u<<1].minn,tr[(u<<1)+1].minn);
tr[u].maxx=max(tr[u<<1].maxx,tr[(u<<1)+1].maxx);
tr[u].sum=tr[u<<1].sum+tr[(u<<1)+1].sum;
}
void build(int u,int l,int r)
{
tr[u]={l,r};
if(l==r)
{
tr[u].maxx=tr[u].minn=tr[u].sum=a[l];
if(a[l]==0)tr[u].maxx=tr[u].minn=99;
return;
}
int mid=l+r>>1;
build(u<<1,l,mid),build((u<<1)+1,mid+1,r);
pushup(u);
}
void modify(int u,int l,int r,int k)
{
if(tr[u].maxx<=100&&tr[u].minn>=99)return;
if(tr[u].l>r||tr[u].r>n>>m;
for(int i=1;i<=n;i++)
{
cin>>a[i];
}
build(1,1,n);
while(m--)
{
cin>>op;
if(op==1)
{
cin>>l>>r>>k;
modify(1,l,r,k);
}
else
{
cout< K本题主要考察了dp
https://ac.nowcoder.com/acm/contest/46800/K
题目分析:
#include
using namespace std;
const int N=1e6+10;
int n,m,a[N],cnt,sum,ans;
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
if(i%3==1)
{
a[i]=1;
cnt++;
}
if(i%3==2)a[i]=0;
if(i%3==0)a[i]=0;
}
int x=n;
while(cnt1)ans++;
}
cout< L本题主要考察了运气
https://ac.nowcoder.com/acm/contest/46800/L
知识点:
算各概率乘次数求和就是期望
题目分析:
由上方定义可以类比出:
第二次猜中是在第一次没猜中的情况下
第i次猜中的前提都是前i-1次没猜中
第一次没猜中 0.8概率(4/5)
第二次猜中 0.25概率(1/5)
第二次猜中的前提是第一次没猜中
由题知:
#include
using namespace std;
int main()
{
cout<<32;
return 0;
} M本题主要考察了找规律
https://ac.nowcoder.com/acm/contest/46800/M
题目分析:
重点在于理解状态转移方程
k是第i个人分到的仙贝数,上一次是第i-1人,分出去了j-k个仙贝,后面加的是好感度,
分的k个/手里有的个数(总共的m-分出的(j-m))
#include
using namespace std;
const int N=1e3+10;
int n,m;
double dp[N][N];
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
for(int j=0;j<=m;j++)
{
for(int k=0;k<=j;k++)
{
dp[i][j]=max(dp[i][j],dp[i-1][j-k]+k*1.0/(m-(j-k)));
}
}
}
printf("%0.9lf",dp[n][m]);
return 0;
}