第六章代码题(一)
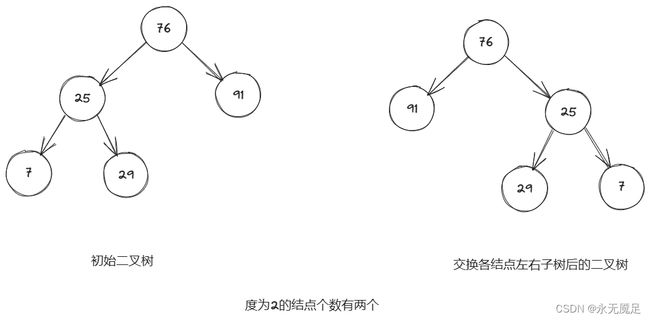
1.求链表存储的二叉树的度为2的结点个数
设置一个变量用来存储度为2的结点的个数,变量增加的条件就是当左右子树都不为空的时候。没有满足条件的就进行递归调用,如果该结点为空就直接返回0。
//求度为2的结点个数
int Getnum(BiTree btree) {
//无结点直接返回
if (btree== NULL)
{
return 0;
}
//k用来记录结点个数
int k = 0;
//度为2的结点个数
if (btree->Lchild!=NULL&&btree->Rchild!=NULL)
{
k++;
}
k += Getnum(btree->Lchild);
k += Getnum(btree->Rchild);
return k;
}2.交换二叉树各结点的左右子树
只要当前结点不为空,管他左右子树为不为空都进行交换。交换后对左右子树进行递归。
有些人可能考虑的比较细致,比如左右子树都为空的话就没必要进行交换。可以依据个人情况对代码进行修改。
//交换二叉树中的各结点的左右子树
BiTree Exchange(BiTree btree) {
if (btree ==NULL)
{
return NULL;
}
//进行交换
BiTnode *curNode = btree->Lchild;
btree->Lchild = btree->Rchild;
btree->Rchild = curNode;
//递归调用
Exchange(btree->Lchild);
Exchange(btree->Rchild);
return btree;
}验证:
1,2题一块验证
#include
#include
#include
#define MaxSize 5
typedef int ElemType;
typedef struct Node {
ElemType data;
struct Node* Lchild;
struct Node* Rchild;
}BiTnode,*BiTree;
//初始化二叉树
void InitTree(BiTree *btree) {
*btree = NULL;
}
//二叉树添加结点
BiTree AddNode(BiTree btree,ElemType value) {
//当前结点值为空
if (btree==NULL)
{
BiTree newNode = (BiTree)malloc(sizeof(BiTnode));
newNode->data = value;
newNode->Lchild = NULL;
newNode->Rchild = NULL;
return newNode;
}
//否则进行判断,值大于根节点往右走
if (value > btree->data)
{
btree->Rchild = AddNode(btree->Rchild, value);
}
//值小于根节点往左走
if (value < btree->data )
{
btree->Lchild = AddNode(btree->Lchild, value);
}
return btree;
}
//遍历
//中序遍历 (左中右)
void MiddleTraversal(BiTree btree) {
if (btree==NULL)
{
return ;
}
MiddleTraversal(btree->Lchild);
printf("%d,", btree->data);
MiddleTraversal(btree->Rchild);
}
//前序遍历 (中左右)
void BeforeTraversal(BiTree btree) {
if (btree == NULL)
{
return;
}
printf("%d,", btree->data);
BeforeTraversal(btree->Lchild);
BeforeTraversal(btree->Rchild);
}
//求度为2的结点个数
int Getnum(BiTree btree) {
//无结点直接返回
if (btree== NULL)
{
return 0;
}
//k用来记录结点个数
int k = 0;
//度为2的结点个数
if (btree->Lchild!=NULL&&btree->Rchild!=NULL)
{
k++;
}
k += Getnum(btree->Lchild);
k += Getnum(btree->Rchild);
return k;
}
//交换二叉树中的各结点的左右子树
BiTree Exchange(BiTree btree) {
if (btree ==NULL)
{
return NULL;
}
BiTnode *curNode = btree->Lchild;
btree->Lchild = btree->Rchild;
btree->Rchild = curNode;
//递归调用
Exchange(btree->Lchild);
Exchange(btree->Rchild);
return btree;
}
int main() {
BiTree btree = (BiTree)malloc(sizeof(BiTnode));
InitTree(&btree);
srand(time(NULL));
for (int i = 0; i < MaxSize; i++)
{
btree=AddNode(btree, rand()%100+1);
}
printf("\n中序遍历\n");
MiddleTraversal(btree);
printf("\n前序遍历\n");
BeforeTraversal(btree);
int num = Getnum(btree);
printf("\n度为2的结点数为%d", num);
Exchange(btree);
printf("\n交换后的中序遍历\n");
MiddleTraversal(btree);
printf("\n交换后的前序遍历\n");
BeforeTraversal(btree);
return 0;
} 执行结果:
由于二叉树在输出窗口不好展示出来,所以利用遍历自己画一下,顺便练练画二叉树的手感。
3.利用叶子结点的空链域,将叶子结点自左向右连成一个单链表
注意该题是利用叶子结点的空链域连接。
其次要找到叶子结点需要进行遍历,实际不论前、中、后遍历,左右子树的遍历相对顺序是一样的,即永远先左再右。所以只需要利用尾插法将其连城一个单链表即可,里面的结点的顺序一定是自左向右的。
这道题思路并不难,但是如果是类似下面这种将指针作为参数而不是全局变量的话就要对指针有更深的理解。
下面的方法中使用了两个指针,一个是用来记录头结点,另外一个是用来进行链表的连接。需要注意的是,在过程中改变的是指针的地址,所以参数类型应该是指向指针的指针变量(指针变量就是用来存储地址的)。head初始为空指针,找到第一个叶子结点后要让head指向它,而p指针指向的地址也在链表添加的过程中不断地变化,因为是递归调用,如果不设置为指向指针的指针,那么在回溯中就有可能出现问题。
//叶子结点的链表组装
//btree为二叉树的结点,head为链表的头指针,为了满足将最左边的叶子结点作为指针返回去,p用来给链表进行添加,指针p的地址需要进行移动
BiTree MergeBNode(BiTree btree,BiTnode **head,BiTnode **p) {
//当前结点为空时,直接进行返回
if (btree == NULL)
{
return NULL;
}
//为叶子结点时
if (btree->Lchild == NULL && btree->Rchild == NULL)
{
//如果链表头结点为空,那么将该叶子结点变为头结点
if (*p == NULL)
{
*p = btree;
*head = *p;
}
//否则就直接添加到链表后面
else {
(*p)->Rchild = btree;
*p = (*p)->Rchild;
}
}
//进行递归,先左后右
MergeBNode(btree->Lchild,head,p);
MergeBNode(btree->Rchild,head,p);
return *head;
}验证:
在前面的验证的基础上增加上面的代码。main函数里需要注意一些细节,比如指针变量的初始化,以及调用函数时的参数类型转换。
int main() {
BiTree btree = (BiTree)malloc(sizeof(BiTnode));
InitTree(&btree);
srand(time(NULL));
for (int i = 0; i < MaxSize; i++)
{
btree=AddNode(btree, rand()%100+1);
}
printf("\n中序遍历\n");
MiddleTraversal(btree);
printf("\n前序遍历\n");
BeforeTraversal(btree);
//创建一个二叉树结点类型的指针并初始化为空
BiTree head = NULL;
BiTnode* p;
p = head;
// &指针变量拿到指针变量的内存地址
MergeBNode(btree,&head,&p);
printf("\n叶子结点组成的链表为\n");
while (head!=NULL)
{
printf(" %d-->", head->data);
head = head->Rchild;
}
return 0;
}执行结果:
示例一:
将二叉树画出来:
示例二:
将二叉树画出来: