【Codeforces】 Codeforces Round #843 (Div. 2)

比赛链接

点击打开链接

官方题解

点击打开链接

Problem A1. Gardener and the Capybaras (easy version)

直接按照题意模拟即可

时间复杂度 ，因为有 的常数，所以可以通过

#include 
using namespace std;
const int N(200100);
int T,n; 
char c[N];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar())
		if(ch=='-')
			RR=-1;
	for(;isdigit(ch);ch=getchar())
		FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
int main(){
	T=read();
	while(T--){
		scanf("%s",c+1);
		n=strlen(c+1);
		bool flg=0;
		for(int i=2;i<=n;i++){
			for(int j=i;j

Problem A2. Gardener and the Capybaras (hard version)

这道题是上道题的加强版

考虑分类讨论

1. 首位是a

首先思考让中间的序列开头为b，末尾的序列开头为a，这样是最简单的情况

找到第一个b出现的位置k1，最后一个a出现的位置k2

如果k1

如果k1>k2，那么这个序列的形式一定是 a…ab…b

那么只要序列分别是 a…ab…b，b，b就可以符合要求

这里需要考虑特殊情况b的个数如果<2

上述构造方式也成立，因为中间的序列一定为a，是最小的

2. 首位是b

构造方式与首位是a类似，不多加赘述

时间复杂度

//考场代码巨丑无比
#include 
using namespace std;
const int N(200100);
int T,n; 
char a[N];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar())
		if(ch=='-')
			RR=-1;
	for(;isdigit(ch);ch=getchar())
		FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
int main(){
	T=read();
	while(T--){
		scanf("%s",a+1);
		n=strlen(a+1);
		if(a[1]=='a'){
			int i=1,j=n;
			for(;i<=n;i++)
				if(a[i]=='b')
					break;
			for(;j;j--)
				if(a[j]=='a')
					break;
			if(i>j){
				if(n-j>=2){//a..abb..b
					for(int k=1;k<=n-2;k++)
						cout<j){
				if(n-j>=2){
					for(int k=1;k<=n-2;k++)
						cout<

Problem B. Gardener and the Array

我们考虑两个集合S1,S2，如果满足 f(S1)=f(S2)

那么它的形式一定是：

我们考虑他们不交的部分，这一部分中出现的所有数一定在另一个集合中出现过

所以其中必有一组数S3每个数都在总的集合中出现了不少于2次

那么构造 f(总集合)=f(总集合去掉S3)

所以只要集合中有一组数中每个数都在总集合中出现了不少于2次，答案就是 Yes

否则就是 No

这里每次清空要当心一下，要记录一下被修改过的位置，否则复杂度就假了

时间复杂度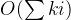

#include 
using namespace std;
const int N(100100),S(200100); 
int T,n,cnt[S];
vector vec[N];
set used;
inline int read(){
   	int FF=0,RR=1;
   	char ch=getchar();
   	for(;!isdigit(ch);ch=getchar())
   		if(ch=='-')
   			RR=-1;
   	for(;isdigit(ch);ch=getchar())
   		FF=(FF<<1)+(FF<<3)+ch-48;
   	return FF*RR;
}
int main(){
   	T=read();
   	while(T--){
   		for(set::iterator it=used.begin();it!=used.end();it++)
    		cnt[*it]=0;
    	used.clear();
    	n=read();
    	for(int i=1,k;i<=n;i++){
    		vec[i].clear();
    		k=read();
    		while(k--){
    			int x=read();cnt[x]++;
    			vec[i].push_back(x);
    			used.insert(x);
    		}
    	}
    	bool ok=0;
    	for(int i=1;i<=n;i++){
    		bool flg=1;
    		for(int j=0;j

Problem C. Interesting Sequence

很明显对于每一位分开来进行考虑

如果n的第i位是0，且x的第i位是1，无解

如果n的第i位是1，且x的第i位是0，答案一定>=最小的第i位是0且>=n的数

如果n的第i位是1，且x的第i位是1，答案一定<最小的第i位是0的>=n的数

时间复杂度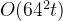

#include 
#define int unsigned long long
using namespace std;
int T,n,x;
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar())
		if(ch=='-')
			RR=-1;
	for(;isdigit(ch);ch=getchar())
		FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
signed main(){
	T=read();
	while(T--){
		n=read(),x=read();
		bool flg=1;
		for(int i=0;i<64&&flg;i++)
			if(!(n>>i&1ll)&&(x>>i&1ll)){
				puts("-1");
				flg=0;
			}
		if(!flg)
			continue;
		int maxi=5e18,mini=n;
		for(int i=0;i<64;i++)
			if(n>>i&1ll){
				if(x>>i&1ll){
					int res=0;
					for(int j=63;j>i;j--){
						int c=n>>j&1ll;
						res+=c*(1ll<i;j--){
						int c=n>>j&1ll;
						res+=c*(1ll<maxi)
			puts("-1");
		else
			printf("%lld\n",mini);
	}
	return 0;
}

Problem D. Friendly Spiders

这道题一条一条连边时间和空间都不够

我们考虑优化建图

我们可以对每一个质因子建一个点

且将每个点与它的质因子之间连双向边

然后在跑bfs就可以了

这个建图优化还是比较基础的

时间复杂度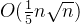， 大约是质因子的密度

#include 
using namespace std;
const int N(600100),inf(0x3f3f3f3f);
int n,s,t,a[N],dp[N],pre[N];
int cnt,v[N],prime[N];
vector vec[N];
queue que;
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar())
		if(ch=='-')
			RR=-1;
	for(;isdigit(ch);ch=getchar())
		FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
void print(int x){
	if(x==0)
		return;
	print(pre[x]);
	if(x<=n)
		printf("%d ",x);
}
int main(){
	for(int i=2;i<=300000;i++){
		if(!v[i])
			v[i]=prime[++cnt]=i;
		for(int j=1;j<=cnt&&i<=300000/prime[j];j++){
			v[prime[j]*i]=prime[j];
			if(prime[j]==v[i])
				break;
		}
	}
	n=read();
	for(int i=1;i<=n;i++)
		a[i]=read();
	for(int i=1;i<=n;i++){
		for(int j=1;prime[j]*prime[j]<=a[i];j++){
			if(a[i]%prime[j]==0){
				while(a[i]%prime[j]==0)
					a[i]/=prime[j];
				vec[i].push_back(prime[j]+n);
				vec[prime[j]+n].push_back(i); 
			}
		}
		if(a[i]>1){
			vec[i].push_back(a[i]+n);
			vec[a[i]+n].push_back(i); 
		}
	}
	s=read(),t=read();
	memset(dp,0x3f,sizeof(dp));
	que.push(s);dp[s]=1;
	while(!que.empty()){
		int u=que.front();
		que.pop();
		for(int i=0;i

Problem E. The Human Equation

这道题乍一看没有任何思路

我们考虑转化数组，可以试一下类似差分，前缀和一类的

这里采用把原数组转化为前缀和数组

对于样例 2 -4 3 -5 4 1

前缀和为 2 -2 1 -4 0 1

我们将 2 3 4 1 奇数位+1，偶数位-1可以变成 3 -4 2 -5 5 0

前缀和为 3 -1 1 -4 1 1

我们发现前缀和数组中[1,2]，[5,5]都+1

多玩几个数据之后可以发现一次操作可以转化成一些区间一起+1或-1

问题转化成了通过一些区间一起+1或-1，最少的操作数使得前缀和数组为0

稍加思考会发现答案是前缀和数组中最大的正数+最小的负数的绝对值

时间复杂度

#include 
#define int long long
using namespace std;
const int N(200100);
int n,a[N];
inline int read(){
	int FF=0,RR=1;
	char ch=getchar();
	for(;!isdigit(ch);ch=getchar())
		if(ch=='-')
			RR=-1;
	for(;isdigit(ch);ch=getchar())
		FF=(FF<<1)+(FF<<3)+ch-48;
	return FF*RR;
}
void work(){
	n=read();
	for(int i=1;i<=n;i++)
		a[i]=read(),a[i]+=a[i-1];
	int maxi=0,mini=0;
	for(int i=1;i<=n;i++){
		maxi=max(maxi,a[i]);
		mini=min(mini,a[i]);
	}
	printf("%lld\n",maxi-mini);
}
signed main(){
	int T=read();
	while(T--)
		work();
	return 0;
}

Problem F. Laboratory on Pluto

不会~