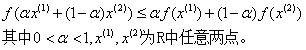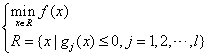数学建模学习笔记——非线性规划

本文章为《数学建模算法与应用（司守奎）》书籍的学习笔记，文章内代码大部分为该书籍的搬运或在网络上的搜集，主要目的为简化阅读的过程，以便直接实现代码的运用，我也会对书中的习题给出自己的解。

一、基础知识储备

1.非线性规划

1.1标准形式

[x,y] = fmincon(fun,x0,A,B,Aeq,Beq,LB,UB,nonlcon,options);
%fun目标函数（新建.m文件），x0为x的初值，A,B,Aeq,Beq为线性约束，LB，UB为边界
%如果无界，可以设置为inf，nonlcon为.m文件定义的非线性约束，C(x)，Ceq(x)。options为优化参数，可以缺省。

1.2凸函数、凸规划

• 凸函数
  类似高中学的凸函数吧，不过这个是这个凸函数应该是像y=x^2之类的函数，只有一个最小值，局部最优解也是整体最优解。

• 凸规划
  f函数为凸函数，g函数也为凸函数，这样的线性规划称为凸规划。

2.无约束问题

2.1一维搜索方法

• Fibonacci 法
  首先写出Fibonacci数列，数列F = [1 1 2 3 5 8 13 21,…]。
  
  我理解的Fibonacci 法的思想是：
  首先确定你最终要求的结果的精度，这里精度又可以理解为最终所剩区间的长度，然后你可以根据最终所剩的区间长度，确定出你要将整个区间分为多少份（即确定出F[n]的n）。
  具体可看下面的图:
  由此可以总结该方法的步骤如下：
  ①选取初始数据，确定单峰区间，[a0,b0]，给出搜索精度，根据公式确定搜索次数n。
  ②计算出最初搜索点t1，t2。
  ③对区间进行搜索。

function y = fibonacci(n)
if n==0||n==1
    y = 1;
else
    y = fibonacci(n-1)+fibonacci(n-2);
end

function [xn,favl,t] = fibosolve(func,B,accuracy)
%func函数句柄，B搜索边界、二维列向量，accuracy搜索终止时的区间精度
%x取最优值时的自变量值，favl最优函数值，t迭代次数
%example [x,favl,t] = fibosolve(@(x)sin(x),[0,5],0.01)

a = B(1);
b = B(2);

c = (b-a)/accuracy;
t = 1;

while fibonacci(t)<c %确定迭代次数
    t = t+1;
end

x1 = a+fibonacci(t-2)/fibonacci(t)*(b-a);%前两个点搜索点的计算公式
x2 = a+fibonacci(t-1)/fibonacci(t)*(b-a);
F1 = feval(func,x1);
F2 = feval(func,x2);

for k = 1:t-1
    if F1<F2            %左边函数值偏小，目标解可能在左区间，和0.618法基本一样
        b = x2;
        x2 = x1;
        F2 = F1;
        x1 = a+fibonacci(t-k-2)/fibonacci(t-k)*(b-a);
        F1 = feval(func,x1);
    else
        a = x1;
        x1 = x2;
        F1 = F2;
        x2 = a+fibonacci(t-k-1)/fibonacci(t-k)*(b-a);
        F2 = feval(func,x2);
    end
end

if F1<F2
    b = x2;
    x2 = x1;
    F2 = F1;
else
    a = x1;
end

x1 = x2-0.1*(b-a);
F1 = feval(func,x1);

if F1<F2
    xn = 0.5*(a+x2);
elseif F1==F2
    xn = 0.5*(x1+x2);
else
    xn = 0.5*(x1+b);
end

favl = feval(func,xn);

• 0.618法
  0.618法和Fibonacci法类似，只是每一次搜后的区间长度变为上一次搜索区间长度的0.618，其第1，2搜索点分别在区间的0.618,0.382处。

function [x,favl,t] = goldensection(func,x0,B,accuracy)

%func函数句柄，x0给定搜索初值吗，B搜索边界、二维列向量，accuracy搜索终止时的区间精度
%x取最优值时的自变量值，favl最优函数值，t迭代次数
%example [x,favl,t] = goldensection(@(x)sin(x),2.5,[0;5],0.1);

r = (sqrt(5)-1)/2; %黄金分割数
a = B(1);          %下界&上界
b = B(2);

a1 = b-r*(b-a);    %黄金分割点，a1左，a2右
a2 = a+r*(b-a);
y1 = feval(func,x0);%黄金分割点函数值
y2 = feval(func,x0);
t = 0;              %迭代次数

while (b-a)>=accuracy
    t = t+1;
    if y1>=y2       %左分割点函数值大，目标解在右区间
        a = a1;
        a1 = a2;
        y1 = y2;    %为什么取黄金分割点，因为黄金分割点的话，搜索下一个区间，只用新计算一个函数值
        a2 = a+r*(b-a);
        y2 = feval(func,a2);
    else
        b = a2;
        a2 = a1;
        y2 = y1;
        a1 = b-r*(b-a);
        y1 = feval(func,a1);
    end
end
x = (a+b)/2;
favl = feval(func,x);
end

• Armijo非等精度搜索方法
  Armijo方法不需要提前知道单凸区间，所以求解问题更加灵活。
  这里直接贴上一个大佬的博客。

2.2二次插值法

function [xmin ,fmin] = erf(f,B,epsilon)
%f函数句柄，B搜索边界、二维列向量，epsilon搜索终止时的区间精度
%example [xmin,fmin] = erf(@(x)exp(x)-2*x,[0 2],0.1)

a = B(1);
b = B(2);
x1 = a;f1 = f(x1);
x3 = b;f3 = f(x3);
x2 = 0.5*(x1+x3);
f2 = f(x2);
c1 = (f3-f1)/(x3-x1);
c2 = ((f2-f1)/(x2-x1)-c1)/(x2-x3);
xp = 0.5*(x1+x3-c1/c2);fp = f(xp);
while (abs(xp-x2)>=epsilon)
    if x2<xp
        if f2>fp
            f1=f2;x1=x2;
            x2=xp;f2=fp;
        else
            f3 = fp;x3 = xp;
        end
    else
        if f2>fp
            f3=f2;x3=x2;
            f2=fp;x2=xp;
        else
            f1=fp;x1=xp;
        end
    end
    c1 = (f3-f1)/(x3-x1);
    c2 = ((f2-f1)/(x2-x1)-c1)/(x2-x3);
    xp = 0.5*(x1+x3-c1/c2);
    fp = f(xp);
end
if f2>fp
    xmin = xp;fmin = f(xp);
else
    xmin = x2;fmin = f(x2);
end
end

2.3无约束问题的极值解法

• 解析法——梯度法，Newton法，变尺度法
  梯度法和Newton法书上有相关的例题和代码，这里不再给出，变尺度法有点抽象，还不能理解。
• 直接法
• matlab函数解法(fminunc,fminsearch函数)
  函数功能直接看官方文档，要知道的是，求函数最优值时，函数也可以包括目标函数的一阶导函数，二阶导函数（hessian矩阵）。

3.约束极值问题

3.1二次规划

只有目标函数是二次的，约束条件全部是线性的。

%求解二次规划的关键是求对实对称矩阵，主要就是根据实际的目标函数求对称阵。
[x,favl] = quadprog(H,f,A,b,Aeq,beq,LB,UB,x0,options);

3.2罚函数法

将约束问题转化为无约束问题，然后利用matlab自带求最优值函数（fmincon，fminsearch）直接求解。

3.3matlab自带函数

• fminbnd（求解单变量函数在定区间上最小值）
• fseminf（求解半无限约束多变量非线性函数的最小值）
• fminimax（求解minimax约束问题）
• fmincon（寻找约束非线性多变量函数最小值）

二、章节习题解答

Q1

%问题1的解法与书中的例题的解法相同，注意到该题是求最大值，故我们对目标函数和导函数取负，最终求得的结果取负即是我们要求的答案。
%定义.m函数文件
function [f,df]=detaf(x)

f=-4*x(1)-6*x(2)+2*x(1)^2+2*x(1)*x(2)+2*x(2)^2; 
df=[-4+4*x(1)+2*x(2);
    -6+2*x(1)+4*x(2)]; 
end

x=[1;1];
[f0,g]=detaf(x);
while norm(g)>0.000001
	p=-g/norm(g);
	t=1.0;f=detaf(x+t*p);
	while f>f0
		t=t/2;
		f=detaf(x+t*p);
	end
	x=x+t*p;
	[f0,g]=detaf(x);
end
x,f0 = -f0

Q2

%老规矩，新建.m文件，保存目标函数，目标函数的导函数，目标函数的hessian矩阵。
function [f,df,d2f]=nwfun(x)
f=-1/(x(1)^2+x(2)^2+2); 
df=[2*x(1)/(x(1)^2+x(2)^2+2)^2;2*x(2)/(x(1)^2+x(2)^2+2)^2]; 
d2f=[(2*(x(1)^2+x(2)^2+2)^2-8*x(1)^2*(x(1)^2+x(2)^2+2))/(x(1)^2+x(2)^2+2)^4,-8*x(1)*x(2)*(x(1)^2+x(2)^2+2)/(x(1)^2+x(2)^2+2)^4 
 -8*x(1)*x(2)*(x(1)^2+x(2)^2+2)/(x(1)^2+x(2)^2+2)^4 ,(2*(x(2)^2+x(1)^2+2)^2-8*x(2)^2*(x(2)^2+x(1)^2+2))/(x(2)^2+x(1)^2+2)^4]; 

%等步长的Newton梯度下降法
x=[4;0];
[f0,g1,g2]=nwfun(x);
while norm(g1)>0.00001 
	p=-inv(g2)*g1;
	x=x+p;
	[f0,g1,g2]=nwfun(x);
end
x,f0

%变步长的Newton梯度下降法（变步长的解较不变步长的解小）
x=[4;0];t = 1;
[f0,g1,g2]=nwfun(x);
while norm(g1)>0.00001 
	p=-inv(g2)*g1;
	x=x+p./t;t = t+1;
	[f0,g1,g2]=nwfun(x);
end
x,f0

Q3

该问题是一个二次规划，关键在于写出目标函数。
设三季度生产的台数分别为x1，x2，x3，则很容易就可以每季度的费用，进一步写出三季度的总费用，根据题目要求写出限制条件。

H = 0.4.*eye(3);
f = [58;54;50];
A = [-1 0 0;-1 -1 0];
b = [-40;-100];
Aeq = [1 1 1];
beq = 180;
lb = zeros(3,1);
ub = 100*ones(3,1);
[x,favl] = quadprog(H,f,A,b,Aeq,beq,lb,ub)

Q4

%该题代码直接搬运自书籍
%新建.m非线性约束条件函数
function [f,g] = fun3_4(x)
% 定义非线性不等式约束函数
g = [];%没有非线性等式约束
th0 = [243 236 220.5 159 230 52]';th = th0+x;
x0 = [150 85 150 145 130 0];
y0 = [140 85 155 50 150 0];
k = 1;
for i = 1:55
    for j = i+1:6
        aij = 4*(sind((th(i)-th(j))/2))^2;
        bij = 2*((x0(i)-x0(j))*(cosd(th(i))-cosd(th(j)))+(y0(i)-y0(j))*(sind(th(i))-sind(th(j))));
        cij = (x0(i)-x0(j))^2+(y0(i)-y0(j))^2-64;
        f(k) = bij^2-4*aij*cij;%前面的只是铺垫，这个才是非线性不等式约束
        k = k+1;
    end
end

fun3_1 = @(delta) sum(delta.^2);%目标函数
[del favl] = fmincon(fun3_1,rand(6,1),[],[],[],[],-30*ones(6,1),30*ones(6,1),@fun3_4)
%del即每架飞机的方向变化量

Q5

Q5、Q6习题解答书中均已有代码，这里不再给出。

Q7

本题参考代码地址
（1）假设人的眼睛的坐标为（x,y），则：

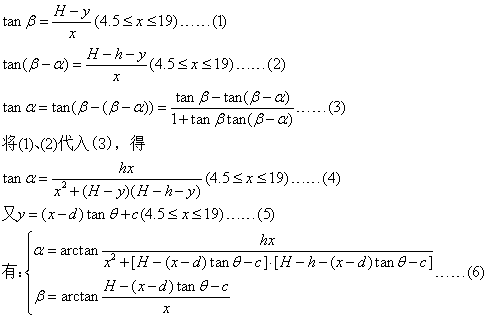
%对于问题1，绘制出alpha，beta随坐标x变化的变化情况，可以看出，alpha，beta随x的增大而减小，假设beta<30度的范围度的舒适程度一样，
%则在保证beta不影响观影体验的情况下，alpha的最大值的位置可以看做最佳观影位置。即beta取得30度时的x即为最佳观影位置。
function [x,alpha,beta] = fun3_7(theta)
%theta座位倾角，角度制

theta = theta/180*pi;
h = 1.8;
H = 5;
d = 4.5;
c = 1.1;
beta = 30/180*pi;
x = (H+d*tan(theta)-c)/(tan(beta)+tan(theta));
alpha = atan((h*x)/(x^2+(H-(x-d)*tan(theta)-c)*(H-h-(x-d)*tan(theta)-c)));
beta = rad2deg(beta);
alpha = rad2deg(alpha);
end

%输出倾角为10度时，beta为30度时的解
[x,theta,beta] = fun3_7(10)

（2）问题二需要使所有观众平均满意程度最大，故需综合考虑beta和theta的大小，因为beta和theta都是角度，所以可以将它们简单的线性加构成新的目标函数。
故目标函数：

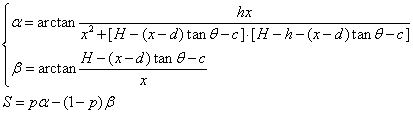
倾角不同，位置不同时S值不同，假设各排的x方向的间隔相等，共有n排，同一排中不同位置的满意程度相同，则目标函数为：

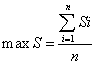
注意到，当beta<=30度时，可以认为beta对目标si没有影响，但是当beta>30度时，必须考虑beta的影响，即对于Si=pα-(1-p)β（Si是一个关于theta和x的函数），当beta<=30度时，p=1，beta>30度时，p可以根据情况任取0~1，这里取0.7。

function y = fun3_72(n,theta)
%n座位排数，theta座位倾角

D = 19;
theta = theta/180*pi;
d = 4.5;
y = 0;

step = (D-d)/(n-1);
x = d:step:D;
for i = x
    y = y+vS(i,theta);
end
y = y/n;

function Si = vS(x,theta)
%xi座位的横坐标，theta座位的倾角

theta = theta/180*pi;
h = 1.8;
H = 5;
d = 4.5;
c = 1.1;

beta = atan((H-(x-d)*tan(theta)-c)/x);
alpha = atan((h*x)/(x^2+(H-(x-d)*tan(theta)-c)*(H-h-(x-d)*tan(theta)-c)));
beta = rad2deg(beta);
alpha = rad2deg(alpha);
if beta<=30
    Si = 0.7*alpha;
else
    Si = 0.7*alpha-0.3*beta;
end
end

x = 10:20;
y = [];
for i = x
y = [y;fun3_72(15,i)];
end
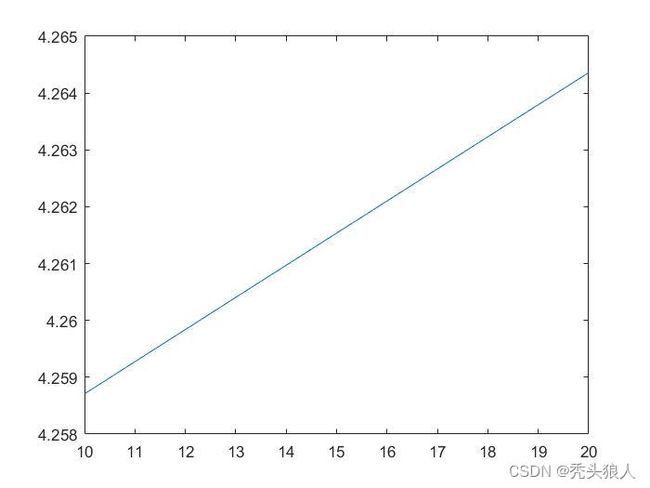
plot(x,y)

对theta不同的情况进行绘图，发现目标函数是一个递增函数，又根据实际情况，最后一排观众的水平视线不应超过屏幕上沿，估计算最优theta如下：

theta = atand((H-c)/(D-d));%解得theta最优为15.0543度

（3）问题三主要考虑，如何改变alpha和beta来提升观众满意度，本篇不做给出。