HDOJ---1018 求N！的位数[斯特林公式---处理阶乘及阶乘位数的问题]

 

Big Number

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 15969    Accepted Submission(s): 7061

Problem Description

In many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number.

 

 

Input

Input consists of several lines of integer numbers. The first line contains an integer n, which is the number of cases to be tested, followed by n lines, one integer 1 ≤ n ≤ 10 ⁷ on each line.

 

 

Output

The output contains the number of digits in the factorial of the integers appearing in the input.

 

 

Sample Input

2 10 20

 

 

Sample Output

7 19

 

 

Source

Asia 2002, Dhaka (Bengal)

 

 

Recommend

JGShining

 

 

 

 

 

 

注意:log()函数默认为loge（），且log(n)中，n必须为float或double型。

code:

 1 /*斯特林[striling]公式(求阶乘(n!)的位数) 

 2 -10-05 13:49

 3 例如1000阶乘位数： 

 4 log10(1)+log10(2)+···+log10(1000)取整后加1 

 5 */

 6 

 7 #include <stdio.h>

 8  #include <math.h>

 9  int main()

10  {

11      int n,cas,i;

12      double sum;

13      scanf("%d",&cas);

14      while (cas--)

15      {

16          scanf("%d",&n);

17          sum=1;

18          for(i=1;i<=n;i++)   

19              sum+=log10((double)i);

20          printf("%d\n",(int)sum);

21      }

22      return 0;

23  }

24 /*

25 或

26 

27 #include<stdio.h> 

28 #include<math.h> 

29 #define PI 3.14159265 

30 int main(){ 

31 int len,N; 

32 while(scanf("%d",&N)!=EOF)

33 {

34 if(N==1)

35 len=1;

36 else

37 len=(int)ceil((N*log(N)-N+log(2*N*PI)/2)/log(10));////ceil求上界，即不小于某值的最小整数 

38 //string公式lnN!=NlnN-N +0.5*ln( 2*N*pi) 

39 //而N次方阶乘的位数等于： 

40 //     log10(N!)取整后加1 

41 //    log10(N!)=lnN!/ln(10) 

42 

43 //ceil为求上界，即不小n的最小整数

44 //log取自然对数

45 printf("%d\n",len); 

46 }

47 return 0;

48 }*/

 

 

 

 

---

斯特林公式---处理阶乘及阶乘位数的问题

1：把n！写成10^m次方的形式，如果m=2，就说明是三位数。

【维基百科】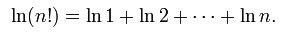

【别处摘来的】可以将n!表示成10的次幂,即n!=10^M(10的M次方，10^2是3位M+1就代表位数)则不小于M的最小整数就是
    n!的位数，对该式两边取对数，有M=log10^n!即：
    M = log10^1+log10^2+log10^3...+log10^n
    循环求和,就能算得M值

，该M是n!的精确位数。

 

 1 #include <stdio.h>

 2  #include <math.h>

 3  int main()

 4  {

 5      int n,cas,i;

 6      double sum;

 7      scanf("%d",&cas);

 8      while (cas--)

 9      {

10          scanf("%d",&n);

11          sum=1;

12          for(i=1;i<=n;i++)    sum+=log10((double)i);

13          printf("%d\n",(int)sum);

14      }

15      return 0;

16  }

 

2：斯特林公式的应用【没用这个，代码是别人的】

 

 

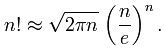
由斯特林[striling]公式可得：lnN!=NlnN－N+0.5ln(2N*pi)

 

而N的阶乘的位数等于：log10(N!)取整后加1

log10(N!)=lnN!/ln(10) 所以len=lnN!/ln(10)+1

 1 #include<iostream>

 2  #include<cmath>

 3  const double PI=3.14159265;

 4  using namespace std;

 5  int main()

 6  {

 7      int t,n;

 8      double sum;

 9      cin>>t;

10      while(t--)

11      {   

12          cin>>n;

13          sum=(n*log(n) - n + 0.5*log(2*n*PI))/log(10)+1;

14          printf("%d/n",(int)sum);   

15      }

16      return 0;

17  }