group convolution (分组卷积)的计算量详解、卷积计算量特征图大小，池化特征图大小、深度通道deep-wise 卷积

group convolution (分组卷积)的计算量详解、卷积计算量特征图大小，池化特征图大小、深度通道deep-wise 卷积

提示：最近忙着各种提前批的笔试面试，所以没太多空刷题了都，先复盘一下各种笔试面试题

---

之前我讲过普通卷积的计算量

看看这个文章：很详细：
【1】卷积神经网络参数量和计算量的计算
【2】复盘：卷积神经网络、池化、乘法运算操作、RNN/transformer/CNN复杂度

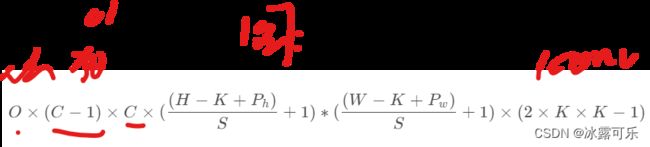
这里我提一下普通卷积的输出尺寸图，这是互联网大厂算法岗必考的笔试题

若图像为正方形：
设输入图像尺寸为WxW，
卷积核尺寸为FxF，
步幅为S，
Padding使用P,
经过该卷积层后输出的图像尺寸为NxN：

若图像为矩形：
设输入图像尺寸为WxH，
卷积核的尺寸为FxF，
步幅为S，
图像深度(通道数)为C，
Padding使用P，
则：卷积后输出图像大小：

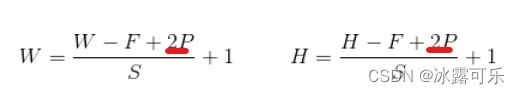
输出图像的通道数就是卷积核的个数
发现了啥没，跟计算量的公式中，卷积次数的公式区别就在：计算量是p，而输出特征图尺寸是2p
【注意，计算量中的K=输出特征图中的F，都是卷积核的个数】
但是计算量那里只需要-p
输出特征图这里需要-2p

因此这俩公式完全可以联合记忆。

再提一嘴池化操作的输出特征图大小，这个互联网大厂也经常考

设输入图像尺寸为WxH，其中W:图像宽，H:图像高，
C:图像深度（通道数），
卷积核的尺寸为FxF，
S:步长
池化后输出图像大小：

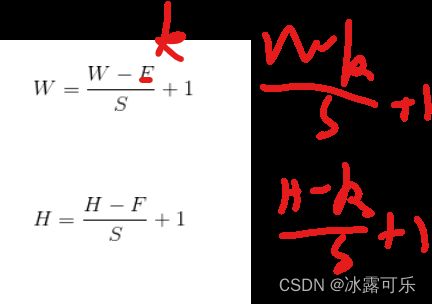
这选择题是经常考的
池化后输出图像深度为C

---

普通卷积

上图为普通卷积示意图，为方便理解，图中只有一个卷积核，此时输入输出数据为：
输入feature map尺寸： W×H×C ，分别对应feature map的宽，高，通道数；
单个卷积核尺寸： k×k×C ，分别对应单个卷积核的宽，高，通道数；
输出feature map尺寸 ：W’×H’ ，输出通道数Cout等于卷积核数量F个，输出的宽和高与卷积步长有关，这里不关心这两个值。

下面这个在上面【1】的基础上，浓缩为大致核心的计算量

k方，主要就是卷积核的计算量，C个通道，卷积核需要刷一遍，输出尺寸w’h’

---

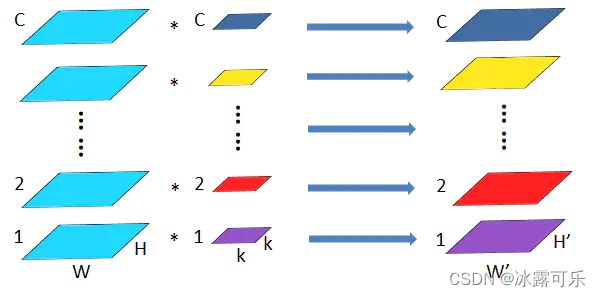
分组卷积（group convolution）

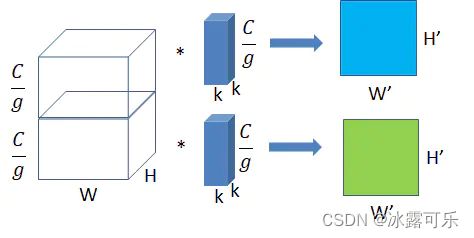将图一卷积的输入feature map 分成g组，
每个卷积核也相应地分成g组，
在对应的组内做卷积，如上图2所示，图中分组数g，
即上面的一组feature map只和上面的一组卷积核做卷积，
下面的一组feature map只和下面的一组卷积核做卷积。
每组卷积都生成一个feature map，共生成g个feature map。

所以group conv常用在轻量型高效网络中，
因为它用少量的参数量和运算量就能生成大量的feature map，
大量的feature map意味着能够编码更多的信息！

深度分离卷积：是目标跟踪的网络中常用的卷积，g=C个，逐个通道卷积，得到C个特征图

如上图所示，深度分离卷积是分组卷积的一种特殊形式，
其分组数g，其中是feature map的通道数C。

即把每个feature map分为一组，分别在组内做卷积，每组内的单个卷积核尺寸为，组内一个卷积核生成一个feature map。

这种卷积形式是最高效的卷积形式，相比普通卷积，用同等的参数量和运算量就能够生成个feature map，而普通卷积只能生成一个feature map。

所以深度分离卷积几乎是构造轻量高效模型的必用结构，
如Xception, MobileNet, MobileNet V2, ShuffleNet, ShuffleNet V2, CondenseNet
等轻量型网络结构中的必用结构。

---

总结

提示：重要经验：

1）普通卷积的计算量，输出尺寸大小，都是互联网大厂必考的东西，顺便看了下池化的输出尺寸图大小
2）分组卷积，实际上就是同样的计算量，得到了更多的特征图，效率高，分组数g=C时就是深度通道卷积Deep-wise CNN
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。