Silverlight 计算机图形学3 三维空间坐标

第一：奇次坐标

为什么要引入齐次坐标呢？这主要是由于以下两方面的原因：
    首先，在物理学中, 矢量用于表示力和速度等物理量， 通常用具有长度和方向的线段来表示，如图4.1表示。我们往往用数学符号 表示一个矢量。它与空间位置无关。对于三维空间中位于(x, y, z)处的一个点P, 如果我们用一个列矩阵 来表示它, 这与矢量的表示会引起混淆。
    其次，在二维或三维空间中，矩阵的乘积，例如Q＝TP，只能表示旋转、比例和剪切等等变换，而不能表示平移变换。



   
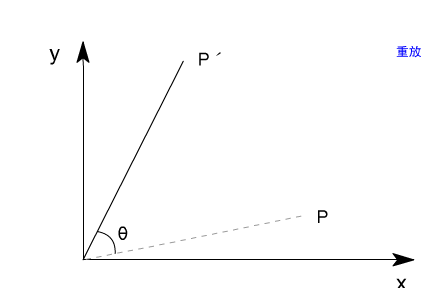
例如, 在图4.2中，点P绕坐标原点旋转θ角后到达P′，其坐标可以用下式计算：
（4－1－1）
　　
其中
　　
。
    对于比例、反射和剪切等变换，我们都可以得到类似（4－1－1）式的矩阵表达式。但是，如果我们将物体沿直线路径从一个坐标位置平移到另一个坐标位置，即通过给原始坐标位置（x,y,z）加上平移距离t _x、t _y和t _z后，使它移到新的位置(x′, y′, z′)。令P＝[x, y, z] ^T, P _t=[t _x , t _y , t _z] ^T, P′＝[x′, y′, z′] ^T, 则
。 （4－1－2）
上式的右边就不能象（4－1－1）式的右边那样写成两个矩阵相乘的形式。
    为了避免这些困难，我们用4维列矩阵来表示三维空间中的点和矢量。假定用（e ₁, e ₂, e ₃, P ₀）指定三维空间坐标系的框架，其中，e ₁, e ₂和e ₃是坐标轴矢量，P ₀是坐标原点。则空间中的任何一个点P都可以在该坐标系框架下唯一地写成
。

我们可以用矩阵乘积的形式把上式改写成
。
严格地讲，上式并不是一个点积或内积，因为其矩阵的元素是不同的。上式右边的4维行矩阵就是P点在给定的坐标系框架下的齐次坐标表示。或者等价地说，P点的齐次坐标可以用4维列矩阵表示为
。
在同一个坐标系框架下，任何矢量V都可以写成

，
于是，V能够用列矩阵表示为 。
应当指出，这个式子几何上有不同的解释，我们在后面还会介绍。


 
仿射变换


仿射变换是计算机图形学中最常用的变换。下列形式的坐标变换称为三维仿射变换：
左（4－2－1）
即：Q的坐标是P的坐标的线性组合。它可以用齐次坐标来表示：
左（4－2－2）
    仿射变换将矢量变换成为矢量。如上一节所述，如果空间矢量V的坐标是V _x, V _y和V _z，它的坐标框架表示（即齐次坐标表示）是一个第4个分量为0的列矢量。它的仿射变换为：
左（4－2－3）
　　可见，矢量V被变换成为另外一个矢量：它的齐次坐标的第4个分量也是0。
（4―2―1）
，

，
。

（4―2―2）
。

（4―2―3）
。

三维几何变换

利用齐次坐标和仿射变换，可以实现所有的三维几何变换。任何复杂的几何变换都可以分解成为比例、剪切、反射、旋转和平移等等简单变换的组合。 4.3.1 比例     在作比例和旋转变换时，都应当指定一个参考点。在此，我们先假定参考点是原点，在4.3.6节中我们将介绍绕任意点的平移和旋转变换。

比例变换是对物体按某种比例进行放大或缩小的一种几何变换。以坐标原点为参考点,沿x、y和z坐标轴分别独立地缩放α _x 、α _y 和α _z 倍的比例变换可以用齐次坐标表示如下（见图4.3）：
P′＝SP
其中，P和P′分别是用齐次坐标表示的变换前和变换后的点，P＝[x y z 1] ^T, P′＝[x′ y′ z′ 1] ^T; S是比例变换矩阵，
（4－3－1）
。
　图4.3 比例变换

其逆变换的变换矩阵
（4－3－2）
。
    对于任何一个三维几何变换，一旦知道了它的变换矩阵（如S），这个变换就唯一确定了。所以，下面我们重点介绍其它几何变换的变换矩阵。