pytorch学习（四）——激活函数
文章目录
- 1. Sigmoid
- 2. Tanh
- 3. ReLU
- 4. LeakyReLU
介绍了模型层后，接下来我们就看看模型层中各种各样的激活函数吧。
激活函数，就是在人工神经网络的神经元上运行的函数，负责将神经元的输入映射到输出端。激活函数对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。
如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。
如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。
以下介绍几种pytorch中常见的激活函数，实际过程中用的都是这四个，其他什么基本没怎么见到。
1. Sigmoid
Sigmoid是将数据限制在0到1之间。但是，由于Sigmoid的最大的梯度为0.25，随着使用sigmoid的层越来越多，网络就变得很难收敛。因此，对深度学习，ReLU及其变种被广泛使用避免收敛困难的问题。
一般在二分类中选择，因为其输出值总在0-1之间，非常符合二分类的特点，Pytorch 中的调用形式为 torch.nn.Sigmoid()。
S i g m o i d Sigmoid Sigmoid 函数的表达式如下：
S i g m o i d ( x ) = σ ( x ) = 1 1 + e − x \begin{aligned} Sigmoid(x)= \sigma(x)=\frac{1}{1+e^{-x}} \end{aligned} Sigmoid(x)=σ(x)=1+e−x1
S i g m o i d Sigmoid Sigmoid 函数的图像如下图所示：
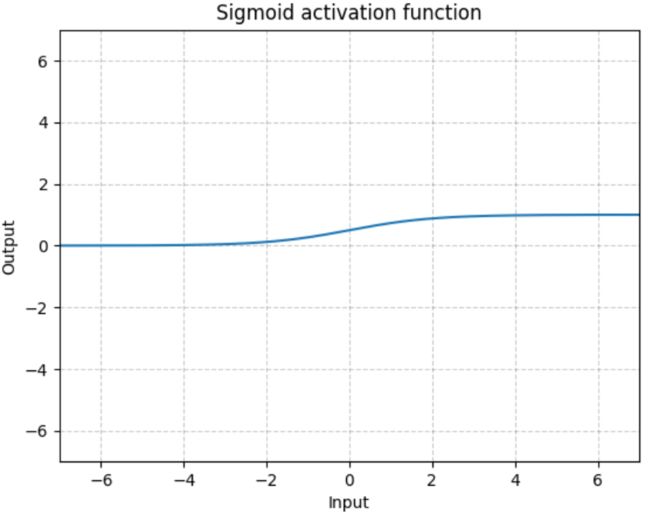
2. Tanh
Tanh就是双曲正切，其输出的数值范围为-1到1，除二分类中，tanh函数总是优于sigmoid函数，Pytorch 中的调用形式为 torch.nn.Tanh()。
T a n h Tanh Tanh 函数的表达式如下：
t a n h ( x ) = e x − e − x e x + e − x \begin{aligned} tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}} \end{aligned} tanh(x)=ex+e−xex−e−x
T a n h Tanh Tanh 函数的图像如下图所示：
3. ReLU
Pytorch 中的调用形式为 torch.nn.ReLU()，在隐藏层上不确定使用哪个激活函数，那么通常会使用Relu激活函数。
R e L U ReLU ReLU 函数的表达式如下：
R e L U ( x ) = { 0 , x ≤ 0 x , x > 0 ReLU(x)=\left\{ \begin{aligned} &0,&x \le 0 \\ &x,&x>0 \end{aligned} \right. ReLU(x)={0,x,x≤0x>0
R e L U ReLU ReLU 函数的图像如下图所示：
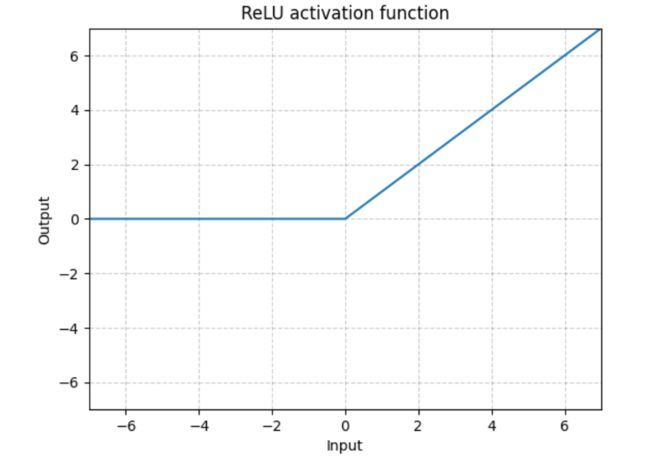
4. LeakyReLU
这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多，Pytorch 中的调用形式为 torch.nn.LeakyReLU()。
L e a k y R e L U LeakyReLU LeakyReLU 函数的表达式如下：
L e a k y R e L U ( x ) = { 0 , x ≤ 0 a x , x > 0 LeakyReLU(x)=\left\{ \begin{aligned} &0,&x \le 0\\ &ax,&x>0 \end{aligned} \right. LeakyReLU(x)={0,ax,x≤0x>0
可以选择是否传入参数 a ，默认是 0.01 0.01 0.01 ，若将 a 改为 0.1 0.1 0.1 ，可以将参数传入为 torch.nn.LeakyReLU(0.1) 。
L e a k y R e L U LeakyReLU LeakyReLU 函数的图像如下图所示：
