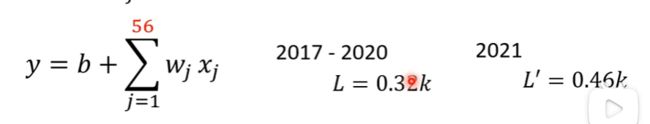【2022机器学习笔记】机器学习基本概念简介P1-P3
1.什么是机器学习（P1，P2）
Machine Learning ≈ Looking for Function（找一个函式）
- Speech Recognition（语音识别）
- image recognition
Deep Learning 的函式是一个类神经网络
Different types of Functions
- 输入可以是向量，矩阵（图片），序列（文章）
- 输出可以是
数值（这种任务叫regression）
类别（classification)
文章 （structured Learning）
机器如何找到函式
-
supervised learning（有监督学习）
tarining data 是有标注的资料 -
self-supervised learning
pre-train:使用unlabled images
Pre-trained Model（也成为Foundation model） 和 Downstream Tasks就类似于Operating Systems 和 Applications
- Reinforcement Learning（强化学习）
2.How to find a function?（P2）
A case study:根据一个频道过往的观看人数预测某天的观看人数
步骤①：写一个带有未知参数的函式（定义模型）
model：函式本身就称为模型
feature：已知参数
weight：和已知参数相乘的变量
bias：剩余的变量
步骤②：定义损失函数Loss(b,w)来评价模型好坏
e表示选定一组(b,w)后，用设定好的函式预测得到的结果与真实值之间的差值
步骤③：Optimization（挑选出可以让loss最小的未知参数(w,b)）
本次课全部使用Gradient Descent（梯度下降）
我们称最好的未知参数为w*，b*
①随机选取一个初始点
②计算微分：
若为正值，则向增大w的值的方向移动
若为负值，则向减小w的值的方向移动
移动的大小由两个参数来决定：微分大小（斜率大小），learning rate（学习速率）
- learning rate由自己设定，这种由自己设定的参数叫做hyperparameters
③更新w参数
何时停止：1.达到设定更新次数 2.在某一点处微分为0
上述步骤都是在training data上做的，我们实际关注的是在testing data上的表现
只考虑前一天的观看人数所得loss：
考虑前7天的观看人数：
考虑前28天的观看人数：
考虑前56天的观看人数：
上述模型（函式）都称为Linear Models
3.改写步骤①（使用flexible model）（P3）
Linear Model太过简单，并不能表示复杂的曲线，所以我们需要更有弹性的模型（flexible model）
对于Linear Model的这种限制，我们成为Model Bias
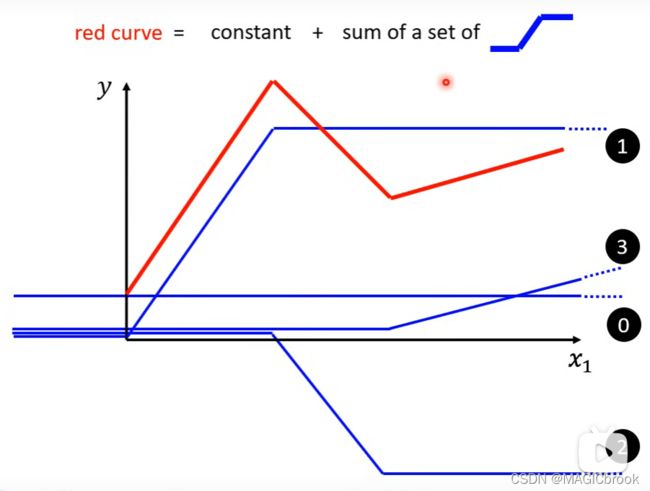
我们使用常数＋许多蓝色函式（Hard Sigmoid）来表示复杂的折线
我们可以用很复杂的折线来逼近曲线，这表示我们可以使用constant和许多蓝色函式来表示复杂的曲线
那么如何表示蓝色函式呢？我们使用Sigmoid Function来表示它
我们可以改变w,b,c的值来表示不同的Sigmoid Function
所以复杂的折线就可以使用许多Sigmoid Function来表示
y = b + ∑ i c i s i g m o i d ( b i + w i x 1 ) y = b + \sum_{i}c_isigmoid(b_i+w_ix_1) y=b+∑icisigmoid(bi+wix1)
上述Function只考虑了一个feature（ x 1 x_1 x1），还可以使用更多的feature来写出函式：
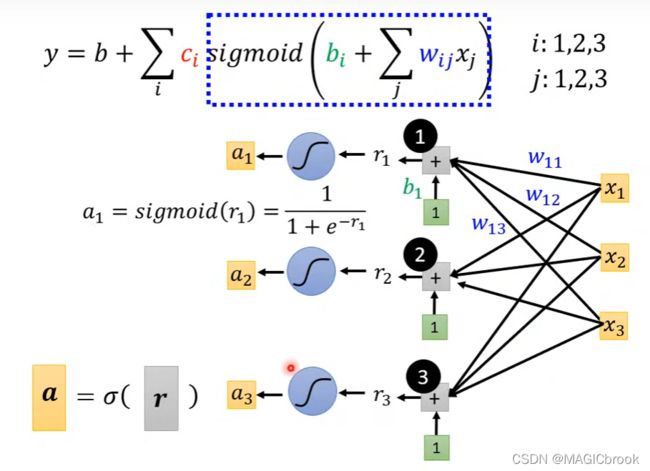
y = b + ∑ i c i s i g m o i d ( b i + ∑ j w i j x j ) y = b + \sum_{i}c_isigmoid(b_i+\sum_j w_{ij}x_j) y=b+∑icisigmoid(bi+∑jwijxj)
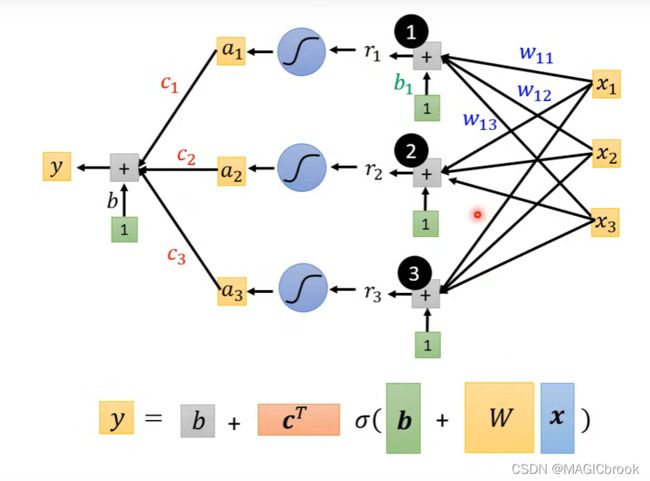
模型y的图示
假设模型中有3个feature，3个sigmoid
蓝色虚线框中的就是
function with unknown parameters
我们将 unknown parameters 排成一列，称为 θ \theta θ
4.Loss
Loss现在是关于 θ \theta θ的函式，用来评价一组 θ \theta θ的好坏
5.optimization of new model
找出可以让loss最小的一组 θ \theta θ，我们称这组 θ \theta θ为 θ ∗ \theta^* θ∗
①随机取初始 θ 0 \theta^0 θ0
②计算 θ 1 \theta_1 θ1， θ 2 \theta_2 θ2， θ 3 \theta_3 θ3…对Loss的微分
③更新 θ \theta θ
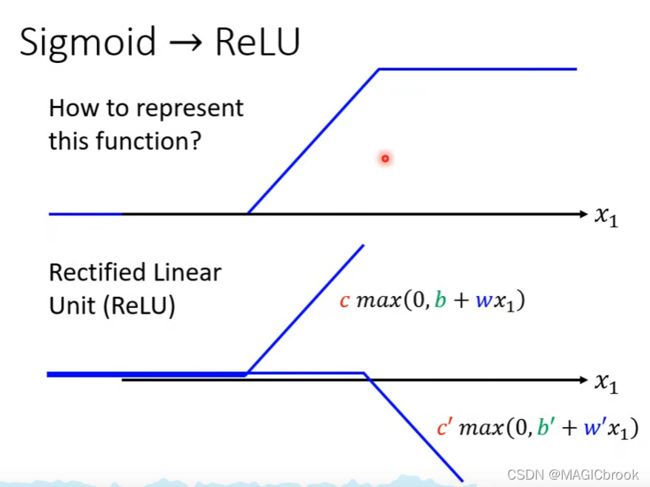
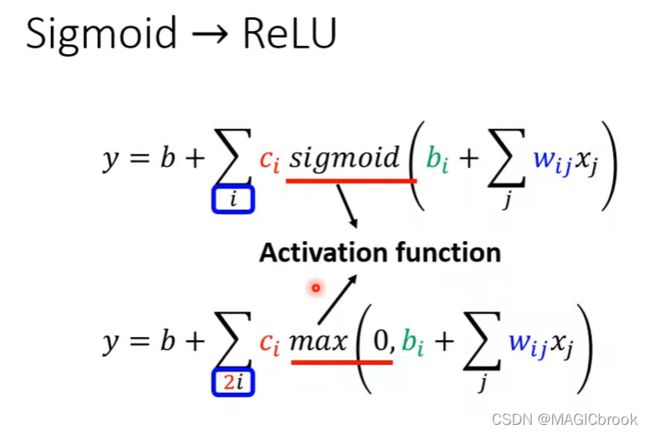
sigmoid也可以用ReLU表示
在机器学习中sigmoid和ReLU都称为Activation function（激活函数）
我们可以继续改写模型,让参数通过多层激活函数
我们将每一层激活函数称为hidden layer
在之前我们说只要sigmoid函数足够的多，那么我们就可以逼近所有复杂的曲线，但是Deep Learning为什么不将所有的sigmoid函数排成一排，而要使用很多层hidden layer呢？
