mae python实现_矩阵分解及代码实现

首先对 Matrix Factorization Techniques for Recommender Systems 这篇论文的核心公式进行讲解和推导；然后用Python代码在Movielens数据集上进行测试实验。

一、算法讲解

1.1 概念描述

假设有

个商品，

个用户，形成一个

维的评分矩阵

， 矩阵

中的元素

表示用户

对商品

的评分。假设潜在特征个数为

，那么

维的矩阵

表示用户的潜在特征矩阵，

用户

的潜在特征向量；

维的矩阵

表示商品的潜在特征矩阵，

商品

的潜在特征向量。

由此，我们可以预测用户

对商品

的评分：

(1)

所以，评分矩阵

可以由两个低秩矩阵

和

来表示：

那么，只要

和

之间的误差尽量小，就能满足实际的需要。所以，目标函数可定义为：

(2)

其中，

表示已经被用户评分过的集合。

1.2 损失函数

对于误差，我们一般使用平均绝对值误差（MAE）或者均方根误差（RMSE）来衡量：

MAE:

RMSE:

其中，

表示被用户评分过的数目。

1.3 公式推导

下面，我们采用RMSE指标，目标函数由等式(2)具体化为：

(3)

为了防止过拟合，即使模型能够有较好的泛化能力，在损失函数中加入正则项，以对参数进行约束：

(4)

公式(4)可以通过概率矩阵分解推导得到，详细步骤可查看以下博客：

周秀泽：概率矩阵分解及MovieLens上的Python代码​zhuanlan.zhihu.com

1.4 求最优解

接下来，我们要对等式(4)求最值了。

等式

分别对

和

进行求导得：

论文中采用的是随机梯度下降法（SGD）进行求解，更新

和

：

其中

为步长，或者称之为学习率。

注意：下降的步长大小非常重要，因为如果太小，则找到函数最小值的速度就很慢，如果太大，则又可能会出现震荡。

令

，上述式子简化为：

(5)

(6)

此处

，为了与论文中的参数统一。

二、 偏置模型 (BiasSVD)

2.1 背景介绍

论文提出：不是所有用户的评分习惯都是一样的，也不是所有商品收欢迎的程度是一样的。有些用户偏向打高分，有些商品很受用户欢迎，所以它们所得到的评分普遍比较偏高。针对这些情况，作者提出了偏置模型，即在矩阵分解的原始模型中加入用户偏置和商品偏置。

2.2 公式讲解

假设用户的偏置为

，商品的偏置为

，我们可以得到：

(7)

其中，

表示全部已有评分数据的均值。

举个例子：让你预测Joe对泰坦尼克号电影的评分。已知全部电影的平均分

。一方面，泰坦尼克号这部电影比一般的电影要好

；另一方面，Joe是一个比较苛刻的用户，他给出的评分比一般用户低

。我们可以估计Joe对泰坦尼克号这部电影的评分为 ：

。

根据等式(7)，我们可以得到用户

对商品

的预测评分：

(8)

对应的目标函数也变为：

(9)

注意：等式(8)和(9)与原论文中的等式(4)和(5)对应。等式(8)中

，而等式(9)中是

。虽然表达不一致，但不影响结果。严谨上来说，等式(9)应该与(8)中一致。

目标函数的优化与上面提到的一样，就不累述了。

三、程序实现

3.1 代码及实现

伪代码如下所示：

Input: the number of latent factor D, the learning rata gamma, 
regularization parameters lambda, the max iteration Step, and the rating matrix R

Initialization: Initialize a random matrix for user matrix p and item matrix q

for t = 1, 2,...Step do
    for (u,i,r) in R
        make prediction pr=qi^T*pu
        error e=r-pr
        update qi and pu by (5) and (6)
        the algorithm suffers a loss (qi, pu, r)
    end for
end for

---

下面用python，在 MovieLens 100K 这个数据集上实现 MF算法。

核心代码如下所示：

def MF(train_list, test_list, N, M, K=10, learning_rate=0.001, lamda_regularizer=0.1, max_iteration=50):
    # train_list: train data 
    # test_list: test data
    # N:the number of user
    # M:the number of item
    # learning_rate: the learning rata
    # K: the number of latent factor
    # lamda_regularizer: regularization parameters
    # max_iteration: the max iteration
    
    P = np.random.normal(0, 0.1, (N, K))
    Q = np.random.normal(0, 0.1, (M, K))
    
    train_mat = sequence2mat(sequence = train_list, N = N, M = M)
    test_mat = sequence2mat(sequence = test_list, N = N, M = M)
    
    records_list = []
    for step in range(max_iteration):
        los=0.0
        for data in train_list:
            u,i,r = data
            P[u],Q[i],ls = update(P[u], Q[i], r=r, learning_rate=learning_rate, lamda_regularizer=lamda_regularizer)
            los += ls
        mae, rmse, recall, precision = evaluation(P, Q, train_mat, test_mat)
        records_list.append(np.array([los, mae, rmse, recall, precision]))
        
        if step % 10 ==0:
            print(' step:%d n loss:%.4f,mae:%.4f,rmse:%.4f,recall:%.4f,precision:%.4f'
                  %(step,los,mae,rmse,recall,precision))
        
    print(' end. n loss:%.4f,mae:%.4f,rmse:%.4f,recall:%.4f,precision:%.4f'
          %(records_list[-1][0],records_list[-1][1],records_list[-1][2],records_list[-1][3],records_list[-1][4]))
    return P,Q,np.array(records_list)


def update(P, Q, r, learning_rate=0.001, lamda_regularizer=0.1):
    error = r - np.dot(P, Q.T)            
    P = P + learning_rate*(error*Q - lamda_regularizer*P)
    Q = Q + learning_rate*(error*P - lamda_regularizer*Q)
    loss = 0.5 * (error**2 + lamda_regularizer*(np.square(P).sum() + np.square(Q).sum()))
    return P,Q,loss

BiasSVD 参考代码：

def update(p, q, bu, bi, aveg_rating, r, learning_rate=0.001, lamda_regularizer=0.1):
    error = r - (aveg_rating + bu + bi + np.dot(p, q.T))            
    p = p + learning_rate*(error*q - lamda_regularizer*p)
    q = q + learning_rate*(error*p - lamda_regularizer*q)
    bu = bu + learning_rate*(error - lamda_regularizer*bu)
    bi = bi + learning_rate*(error - lamda_regularizer*bi)
    return p, q, bu, bi

3.2 实验结果

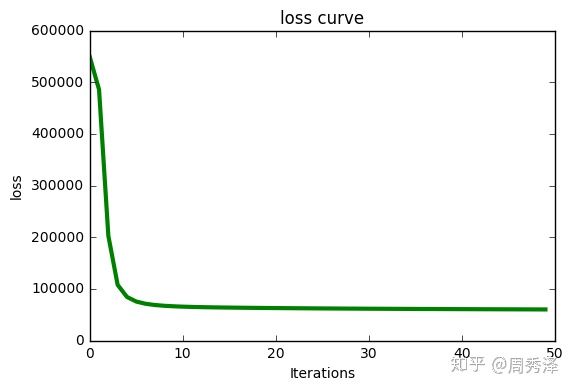
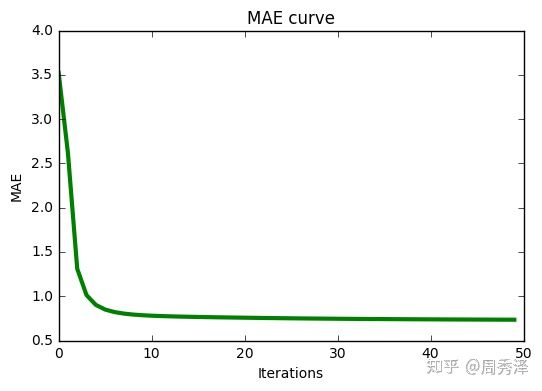
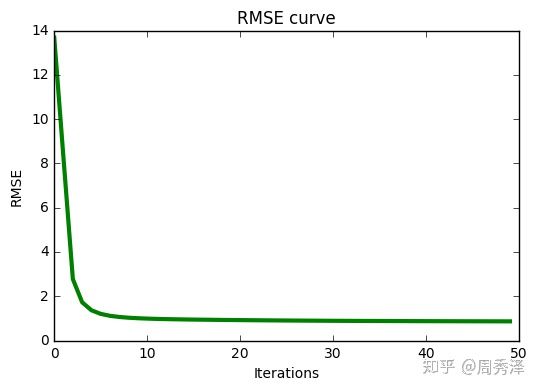
当训练集：测试集=8:2时，可得到 MAE=0.7279 RMSE=0.9229

实验曲线如下所示：

图 2： 迭代过程中的 loss 值

图 3： 迭代过程中的 MAE 值

图 4: 迭代过程中的 RMSE 值

完整项目下载地址：

XiuzeZhou/Recommender-Systems​github.com

更多 矩阵分解内容和程序，请看我的最新博文：

周秀泽：推荐系统系列之二：矩阵分解家族​zhuanlan.zhihu.com

参考资料：

参考资料：

[1] 周秀泽，概率矩阵分解及MovieLens上的Python代码