【西瓜书笔记】4. 支持向量机

4.1 超平面

$${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$$

1. 法向量恒垂直于超平面
2. 和法向量方向相同的点(与$\mathbf{w}$夹角$\theta$小于90度的向量)代入超平面方程恒大于等于0，否则恒小于等于0 (与$\mathbf{w}$夹角$\theta$大于90度的向量)
3. 法向量和位移项唯一确定一个超平面
4. 等倍缩放法向量和位移项超平面不变。

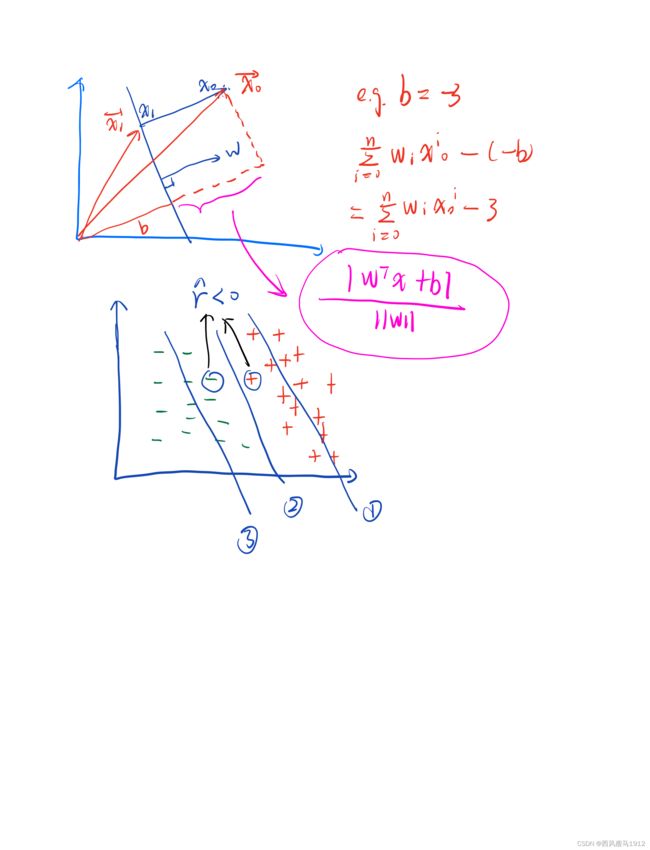
点到超平面距离公式推导

证明：
$$r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right|}{\Vert \mathbf{w}\Vert }$$

首先我们设点$x_0$到超平面的距离为$r$，在超平面上的投影为$x_1$， 那么法向量$w$一定与向量${\mathbf{x}}_1{\mathbf{x}}_0$平行。此时若考虑求两个向量内积的绝对值可得
$$\left|{\mathbf{w}}^{\mathrm{T}}\cdot {\mathbf{x}}_1{\mathbf{x}}_0\right|=\Vert \mathbf{w}\Vert \cdot |\pm 1|\cdot \Vert {\mathbf{x}}_1{\mathbf{x}}_0\Vert =\Vert \mathbf{w}\Vert \cdot r$$
又因为${\mathbf{x}}_0,{\mathbf{x}}_1,\mathbf{w}\in R^n$
$$\begin{array}{rl}{\mathbf{w}}^{\mathrm{T}}\cdot {\mathbf{x}}_1{\mathbf{x}}_0& =w_1\left(x_0^1-x_1^1\right)+w_2\left(x_0^2-x_1^2\right)+\dots +w_n\left(x_0^n-x_1^n\right)\\ & =w_1{x}_0^1+w_2{x}_0^2+\dots +w_n{x}_0^n-\left(w_1{x}_1^1+w_2{x}_1^2+\dots +w_n{x}_1^n\right)\\ & =w_1{x}_0^1+w_2{x}_0^2+\dots +w_n{x}_0^n-(-b)\\ & =w_1{x}_0^1+w_2{x}_0^2+\dots +w_n{x}_0^n+b={\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\end{array}$$
【可以理解${\mathbf{x}}_0$这个从坐标原点为起点的向量先投影在法向量$\mathbf{w}$上，然后减去$b$这个原点到超平面的距离，就得到了${\mathbf{x}}_1{\mathbf{x}}_0$在法向量上的投影长度】

所以
$$\begin{gathered} \left|{\mathbf{w}}^{\mathrm{T}}\cdot {\mathbf{x}}_1{\mathbf{x}}_0\right|=\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_0+b\right|=\Vert \mathbf{w}\Vert \cdot r \\ \Rightarrow r=\frac{\left|{\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right|}{\Vert \mathbf{w}\Vert } \end{gathered}$$

4.2 SVM主问题

函数间隔

我们又定义函数间隔：给定数据集$D=\left\{\left({\mathbf{x}}_1,y_1\right)\cdot \left({\mathbf{x}}_2,y_2\right)\dots \left({\mathbf{x}}_m\cdot y_m\right)\right\},y_i\in \{-1,+1\}$和超平面${\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b=0$。这里$y_i$表示样本标签值。定义超平面关于样本$\left({\mathbf{x}}_i,y_i\right)$的函数间隔为
$${\hat{\gamma }}_i=y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)$$
定义超平面关于数据集的间隔函数为超平面关于数据集中所有样本的函数间隔最小值，也就是
$$\hat{\gamma }=\underset{1,2,\dots ,m}{\min }{\hat{\gamma }}_i$$
此时，样本数据集合超平面有如上图三种情况：

1. 穿过正样本集合。于是位于超平面下方的正样本: $y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)<0\Rightarrow \hat{\gamma }<0$.
2. 穿过正负样本集合之间。于是正负样本都满足: $y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)\ge 0\Rightarrow \hat{\gamma }\ge 0$
3. 穿过负样本集合。于是位于超平面上方的负样本: $y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)<0\Rightarrow \hat{\gamma }<0$

显然一个好的超平面应该同时满足：

1. 完美分开正负样本集合
2. 尽可能同时远离正负样本集合

如果只是优化$\hat{\gamma }$, 也就是最大化$\hat{\gamma }$（$\text{max}\hat{\gamma }$）， 让所有的$\widehat{{\gamma }_i}$都大于等于0，只能保证第一点。

因为如果我们对超平面的法向量和位移项进行等倍缩放，超平面本身是不会变的，但是公式(6)中的$\hat{\gamma }$会等倍缩放。
$$\lambda {\hat{\gamma }}_i=y_i\left(\lambda {\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+\lambda b\right)$$
【也即是说我们可以在固定超平面的情况下，无限放大$\hat{\gamma }$，我们求出$\text{max}\hat{\gamma }$只能保证分开正负样本集合，无法保证超平面在正负样本正中间。为了实现第二点，我们要把这个缩放效应从优化过程中去除掉，因此我们要引入几何间隔概念。】

几何间隔

定义几何间隔：定义超平面关于样本$\left({\mathbf{x}}_i,y_i\right)$的几何间隔为
$${\gamma }_i=\frac{{\hat{\gamma }}_i}{\Vert \mathbf{w}\Vert }=\frac{\lambda {\hat{\gamma }}_i}{\lambda \Vert \mathbf{w}\Vert }$$
同样，定义超平面关于数据集的几何间隔为超平面关于数据集中所有样本的几何间隔最小值，也就是
$$\gamma =\underset{1,2,\dots ,m}{\min }{\gamma }_i=\frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }$$
此时针对$\gamma$优化到最大值，就能保证超平面在正负样本集合的正中间。因为此时我们优化的对象是距离超平面最近的样本点投影到超平面法向量上的距离，让最近点离超平面尽可能远
$$\gamma =\frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }=\frac{y_{min}({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_{min}+b)}{\Vert \mathbf{w}\Vert }=\frac{\left|{\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_{min}+b\right|}{\Vert \mathbf{w}\Vert }$$

SVM的核心思想：求一个与已知数据集几何间隔最大的那个超平面，也就是
$$\begin{array}{rl}\max & \gamma \\ \text{ s.t. }& {\gamma }_i\ge \gamma ,i=1,2,\dots ,m\\ \Rightarrow \max & \frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& \frac{{\gamma }_i}{\Vert \mathbf{w}\Vert }\ge \frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert },i=1,2,\dots ,m\\ \Rightarrow \max & \frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\ge \hat{\gamma },i=1,2,\dots ,m\\ \Rightarrow \max & \frac{1}{\Vert \mathbf{w}\Vert }\\ \text{ s.t. }& y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\ge 1,i=1,2,\dots ,m\\ \Rightarrow \underset{\mathbf{w},b}{\min }& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& 1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩽0,i=1,2,\dots ,m\end{array}$$
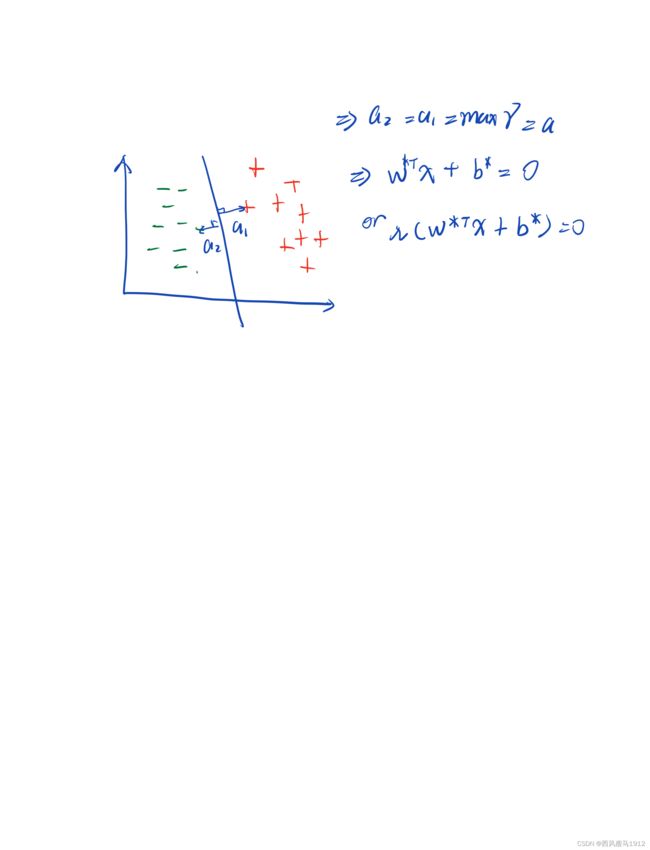
【这里从第二步到第三步有个小细节要注意。因为针对一个超平面，假设正负样本离超平面最近距离分别是$a_1$和$a_2$, 那么优化后应该有$a_1=a_2=\max \gamma$.假设此时的超平面参数满足：
$$\lambda {\mathbf{w}}^{\ast T}\mathbf{x}+\lambda b^{\ast }=0$$
我们可以发现无法确认一组确定的超平面参数${\mathbf{w}}^{\ast },b^{\ast }$, 因为一个超平面无法确认一组参数！其根本原因是，我们对参数缩放$\lambda$倍的时候，$\hat{\gamma }$和$\Vert \mathbf{w}\Vert$也被缩放了$\lambda$倍。也就是优化目标$\frac{\hat{\gamma }}{\Vert \mathbf{w}\Vert }=\frac{\lambda \hat{\gamma }}{\lambda \Vert \mathbf{w}\Vert }$，还有$\text{ s.t. }{y}_i\lambda \left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\ge \lambda \hat{\gamma }$. 所以无法优化出唯一解。为了打破“平衡”，要对平面参数或者$\hat{\gamma }$进行约束。因为对平面参数约束增加求解难度，所以我们第二步到第三步将$\hat{\gamma }=1$设为常数。】

此优化问题本身就是一个很容易求解的凸优化问题，但是还是要用拉格朗日对偶求解。

1. 转化为对偶问题后，对偶问题也很容易求解，同时还能很自然的引入核函数
2. 对偶问题的求解复杂度跟样本个数m成正比，主问题的求解复杂度跟参数(w, b)维度成正比。所以当样本个数远小于参数维度的时候用拉格朗日对偶问题求解效率更高. 【这里主问题要解的是$w,b$，维度如果分别是d维和1维，复杂度总共是d+1维。】

在scikit-learn的dual参数就是关于这第二点进行设置的。反过来，如果不满足这两个条件，尤其是样本个数很大时，用不用对偶求解区别不大。所以dual=False, if n_samples>n_features.

4.3 拉格朗日对偶

对偶函数

$$\begin{array}{ll}\underset{\mathbf{x}}{\min }& f(\mathbf{x})\\ \text{ s.t. }& g_i(\mathbf{x})\le 0(i=1,\dots ,m)\\ & h_j(\mathbf{x})=0(j=1\dots n)\end{array}$$

设定义域为：$D=\mathrm{dom}f\cap {\bigcap }_{i=1}^{m}dom{g}_i\cap {\bigcap }_{j=1}^{n}dom{h}_j$, 同时可行集为：$\tilde{D}=\left\{\mathbf{x}\mid \mathbf{x}\in D,g_i(\mathbf{x})\le 0.h_j(\mathbf{x})=0\right\}$ 【这里m, n不是样本数】

拉格朗日对偶函数$\Gamma$（以拉格朗日乘子($\mu ,\lambda$)为自变量的函数）：
$$\Gamma (\mathbf{\mu },\mathbf{\lambda })=\underset{\mathbf{x}\in D}{\inf }L(\mathbf{x},\mathbf{\mu },\mathbf{\lambda })=\underset{\mathbf{x}\in D}{\inf }\left(f(\mathbf{x})+\sum _{i=1}^m{\mu }_i{g}_i(\mathbf{x})+\sum _{j=1}^n{\lambda }_j{h}_j(\mathbf{x})\right)$$
【inf:下确界，函数下界的最大值，下确界和最小值不完全等价】

【$\mathbf{\mu }=({\mu }_1,{\mu }_2,\cdots ,{\mu }_m)\in R^m,\mathbf{\lambda }=({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_n)\in R^n$】

1. 拉格朗日对偶函数恒为凹函数 ，加个符号就成了凸函数。【上面一开始的三个式子是一般问题，既没有限定是凸函数或者是凹函数。也就是说通过构建拉格朗日对偶函数来解决原来的一般问题，解决原始的三个一般式的最优解】
2. 当$\mu \ge 0$时，拉格朗日对偶函数构成了优化问题最优值$\min f(x)$的下界。

我们来证明第2点：

因为当$\mu \ge 0$时， 对于可行集中的点$\tilde{x}\in \tilde{D}$, 下式恒成立：
$$\sum _{i=1}^n{\mu }_i{g}_i(\tilde{\mathbf{x}})+\sum _{j=1}^m{\lambda }_j{h}_j(\tilde{\mathbf{x}})\le 0$$
又根据拉格朗日函数定义，所以我们有
$$f(\tilde{\mathbf{x}})+\sum _{i=1}^m{\mu }_i{g}_i(\tilde{\mathbf{x}})+\sum _{j=1}^n{\lambda }_j{h}_j(\tilde{\mathbf{x}})\le f(\tilde{\mathbf{x}})$$
又因为$\tilde{D}\in D$, 所以可行集中的拉格朗日函数最小值一定大于等于定义域上拉格朗日函数的下确界，也就是${\inf }_{\mathbf{x}\in D}L(\mathbf{x},\mathbf{\mu },\mathbf{\lambda })\le L(\tilde{\mathbf{x}},\mathbf{\mu },\mathbf{\lambda })$

所以我们有
$$\begin{gathered} \Gamma (\mathbf{\mu },\mathbf{\lambda })=\underset{\mathbf{x}\in D}{\inf }L(\mathbf{x},\mathbf{\mu },\mathbf{\lambda })\le L(\tilde{\mathbf{x}},\mathbf{\mu },\mathbf{\lambda })\le f(\tilde{\mathbf{x}}) \\ \Gamma (\mathbf{\mu },\mathbf{\lambda })\le \min \{f(\tilde{\mathbf{x}})\}=p^{\ast } \end{gathered}$$
因此拉格朗日对偶函数就是优化问题$f(\tilde{\mathbf{x}})$最优值$p^{\ast }$的下界。于是我们接下来就要知道对偶函数的最大值$d^{\ast }$是什么。

拉格朗日对偶问题

求对偶函数最大值的优化问题为拉格朗日对偶问题：
$$\begin{array}{cl}\underset{\mathbf{\mu },\mathbf{\lambda }}{\max }& \Gamma (\mathbf{\mu },\mathbf{\lambda })\\ \text{ s.t. }& \mathbf{\mu }\ge 0\end{array}$$
设该优化问题的最优值为$d^{\ast }$, 显然$d^{\ast }\le p^{\ast }$， 此时称为“弱对偶性”成立。如果$d^{\ast }=p^{\ast }$,则称为“强对偶性”成立。

slater条件：若主问题是凸优化问题，且可行集中存在一点能使得所有不等式约束的不等 号成立，则强对偶性成立。【强对偶性成立的条件不光slater条件】

我们先求SVM的对偶函数:
$$\begin{array}{rl}\Gamma (\mathbf{\mu },\mathbf{\lambda })& =\underset{\mathbf{x}\in D}{\inf }L(\mathbf{x},\mathbf{\mu },\mathbf{\lambda })=\underset{\mathbf{x}\in D}{\inf }\left(f(\mathbf{x})+\sum _{i=1}^m{\mu }_i{g}_i(\mathbf{x})+\sum _{j=1}^n{\lambda }_j{h}_j(\mathbf{x})\right)\\ & =\underset{w,b\in D}{\inf }\left(\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i\left(1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)\right)\right)\\ & =\underset{\mathbf{w},b\in D}{\inf }\left(\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\right)\\ & =\underset{w,b\in D}{\inf }\left(\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i-b\sum _{i=1}^m{\alpha }_i{y}_i\right)\end{array}$$
此时，因为b可以取正负无穷，所以如果${\sum }_{i=1}^m{\alpha }_i{y}_i\ne 0$ ，对偶函数就会取到正负无穷。所以
$$\Gamma (\mathbf{\mu },\mathbf{\lambda })=\{\begin{array}{ll}{\inf }_{w\in D}\left\{\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+{\sum }_{i=1}^m{\alpha }_i-{\sum }_{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i\right\},& \text{ if }{\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ -\infty ,& \text{ otherwise }\end{array}$$
【这里又要注意，因为$1-y_i\left({\mathbf{w}}^T{\mathbf{x}}_i+b\right)⩽0,i=1,2,\dots ,m$中的不等式数量又变回了样本数量，所以这里m代表样本数量】

所以对偶问题转化为:
$$\begin{array}{rl}& \underset{\alpha }{\max }\{\begin{array}{ll}{\inf }_{w\in D}\left\{\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+{\sum }_{i=1}^m{\alpha }_i-{\sum }_{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i\right\},& \text{ if }{\sum }_{i=1}^m{\alpha }_i{y}_i=0\\ -\infty ,& \text{ otherwise }\end{array}\\ & \text{ s.t. }\mathbf{\alpha }\ge 0\end{array}$$
也就是:
$$\begin{array}{ll}{\max }_{\alpha }& {\inf }_{w\in D}\left\{\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+{\sum }_{i=1}^m{\alpha }_i-{\sum }_{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i\right\}\\ \text{ s.t. }& \mathbf{\alpha }\ge 0\\ & {\sum }_{i=1}^m{\alpha }_i{y}_i=0\end{array}$$
其中:
$$\begin{array}{rl}& \underset{\mathbf{w}\in D}{\inf }\left\{\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i\right\}\\ =& \underset{\mathbf{w}\in D}{\min }\left\{\frac{1}{2}\Vert \mathbf{w}{\Vert }^2+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{\mathbf{w}}^T{\mathbf{x}}_i\right\}\\ =& \sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\end{array}$$
对第二行求偏导得到关于$w$的解$\mathbf{w}={\sum }_{i=1}^m{\alpha }_i{y}_i{\mathbf{x}}_{\mathbf{i}}$，然后代入回去即可。而且因为括号中整个式子是个凸函数，inf=min。

所以，SVM的对偶问题的具体形式为：
$$\begin{array}{ll}{\max }_{\alpha }& {\sum }_{i=1}^m{\alpha }_i-\frac{1}{2}{\sum }_{i=1}^m{\sum }_{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{\mathbf{x}}_i^T{\mathbf{x}}_j\\ \text{ s.t. }& \mathbf{\alpha }\ge 0\\ & {\sum }_{i=1}^m{\alpha }_i{y}_i=0\end{array}$$
这个就是西瓜书中的式6.11。

引入对偶问题解决svm的理由：

1. 这里我们有了${\mathbf{x}}_i^T{\mathbf{x}}_j$,可以引入核函数
2. 这里的$\mathbf{\alpha }\in R^m$,维数大小与样本个数相同。求解复杂度与样本个数成正比

KKT条件

SVM的对偶问题的具体形式不光满足以上两个s.t.条件，还满足KKT条件(一个局部最优解的必要条件)。

针对优化问题：
$$\begin{array}{ll}\min & f(x)\\ \text{ s.t. }& g_i(x)\le 0(i=1,\dots ,m)\\ & h_j(x)=0(j=1,\dots ,n)\end{array}$$
设$f(x),g_i(x),h_j(x)$具有连续的一阶偏导数，$x^{\ast }$是局部问题的最优解且满足约束限制条件，那么一定存在拉格朗日乘子${\mathbf{\mu }}^{\ast }={\left({\mu }_1^{\ast },{\mu }_2^{\ast },\dots ,{\mu }_m^{\ast }\right)}^T,{\mathbf{\lambda }}^{\ast }={\left({\lambda }_1^{\ast },{\lambda }_2^{\ast }\dots ,{\lambda }_u^{\ast }\right)}^T$使得：
$$\{\begin{array}{l}{\nabla }_{x}L\left({\mathbf{x}}^{\ast },{\mathbf{\mu }}^{\ast },{\mathbf{\lambda }}^{\ast }\right)=\nabla f\left({\mathbf{x}}^{\ast }\right)+{\sum }_{i=1}^m{\mu }_i^{\ast }\nabla g_i\left({\mathbf{x}}^{\ast }\right)+{\sum }_{j=1}^n{\lambda }_j^{\ast }\nabla h_j\left({\mathbf{x}}^{\ast }\right)=0\\ h_j\left({\mathbf{x}}^{\ast }\right)=0\\ g_i\left({\mathbf{x}}^{\ast }\right)\le 0\\ {\mu }_i^{\ast }\ge 0\\ {\mu }_i^{\ast }{g}_i\left({\mathbf{x}}^{\ast }\right)=0\end{array}$$
（约束限制条件有哪些，可参考文献:王燕军, 梁治安. 最优化基础理论与方法[M]. 复旦大学出版社, 2011.）

以上就是KKT条件。

回到SVM
$$\begin{array}{ll}{\min }_{\mathbf{w},b}& \frac{1}{2}\Vert \mathbf{w}{\Vert }^2\\ \text{ s.t. }& 1-y_i\left({\mathbf{w}}^{\mathrm{T}}{\mathbf{x}}_i+b\right)⩽0,i=1,2,\dots ,m\end{array}$$
SVM问题本身是个凸优化问题，只有一个唯一的全局解，所以我们要求解的(${\mathbf{w}}^{\ast },{\mathbf{b}}^{\ast }$)就是KKT条件中的${\mathbf{x}}^{\ast }$。如果KKT条件要成为(${\mathbf{w}}^{\ast },{\mathbf{b}}^{\ast }$)的必要条件的话，要满足可导和约束限制条件。Slater条件就是其中之一。所以全局最优解(${\mathbf{w}}^{\ast },{\mathbf{b}}^{\ast }$)一定满足KKT条件。

SVM的KKT条件（充分+必要。充分性的证明参见参考文献中的定理4.4.4）：
$$\{\begin{array}{l}{\nabla }_{\mathbf{w},b}L\left({\mathbf{w}}^{\ast },b^{\ast },{\mathbf{\alpha }}^{\ast }\right)={\nabla }_{\mathbf{w},b}\left(\frac{1}{2}{\Vert {\mathbf{w}}^{\ast }\Vert }^2+{\sum }_{i=1}^m{a}_i\left(1-y_i\left({\mathbf{w}}^{\ast T}{x}_i+b^{\ast }\right)\right)\right)=0\\ 1-y_i\left({\mathbf{w}}^{\ast T}{\mathbf{x}}_i+b^{\ast }\right)\le 0\\ a_i^{\ast }\ge 0\\ a_i^{\ast }\left(1-y_i\left({\mathbf{w}}^{\ast T}{\mathbf{x}}_i+b^{\ast }\right)\right)=0\end{array}$$
而且KKT条件是SVM全局最优解的充分条件。