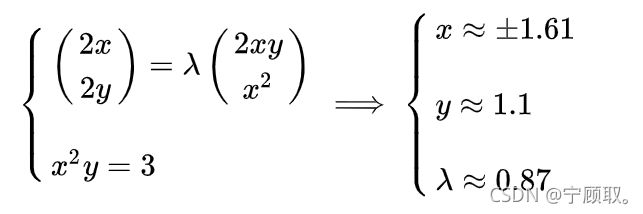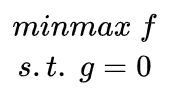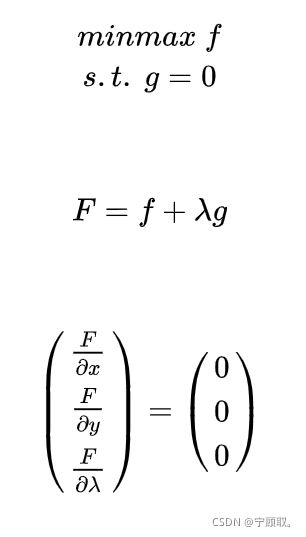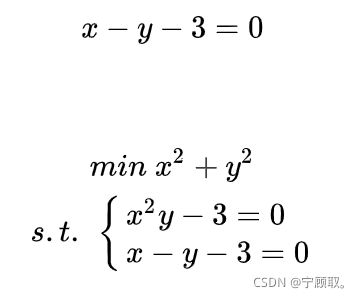SVM原理笔记及代码实现

目录

一.SVM

1.1 SVM简介

1.2 SVM基本概念

1.3 SVM应用实例

1.3.1 线性基础案例

1.3.2  线性相关展示图案例

1.3.3 高斯核

二.相关知识补充

1.拉格朗日乘子法

1.1 求解

1.2 定义

1.3 变形

2.对偶问题（KKT条件）

 3.核函数（高斯核）

---

一.SVM

1.1 SVM简介

支持向量机（support vector machines，SVM）是一种二分类模型，它将实例的特征向量映射为空间中的一些点，SVM 的目的就是想要画出一条线，以 “最好地” 区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。SVM 适合中小型数据样本、非线性、高维的分类问题。

1.2 SVM基本概念

将实例的特征向量（以二维为例）映射为空间中的一些点，如下图的实心点和空心点，它们属于不同的两类。SVM 的目的就是想要画出一条线，以“最好地”区分这两类点，以至如果以后有了新的点，这条线也能做出很好的分类。

1.效果最好的线就是具有 “最大间隔的划分超平面”。

2.画线的标准：SVM 将会寻找可以区分两个类别并且能使间隔（margin）最大的划分超平面。比较好的划分超平面，样本局部扰动时对它的影响最小、产生的分类结果最鲁棒、对未见示例的泛化能力最强。

3.对于任意一个超平面，其两侧数据点都距离它有一个最小距离（垂直距离），这两个最小距离的和就是间隔。比如下图中两条虚线构成的带状区域就是 margin，虚线是由距离中央实线最近的两个点所确定出来的（也就是由支持向量决定）。但此时 margin 比较小，如果用第二种方式画，margin 明显变大也更接近我们的目标。

4.要让 margin 尽量大，大 margin 犯错的几率比较小。

1.3 SVM应用实例

1.3.1 线性基础案例

# sklearn 库中导入 svm 模块
from sklearn import svm

# 定义三个点和标签
X = [[2, 0], [1, 1], [2,3]]
y = [0, 0, 1]
# 定义分类器，clf 意为 classifier，是分类器的传统命名
clf = svm.SVC(kernel = 'linear')  # .SVC（）就是 SVM 的方程，参数 kernel 为线性核函数
# 训练分类器
clf.fit(X, y)  # 调用分类器的 fit 函数建立模型（即计算出划分超平面，且所有相关属性都保存在了分类器 cls 里）
# 打印分类器 clf 的一系列参数
print(clf)
# 支持向量
print(clf.support_vectors_)
# 属于支持向量的点的 index 
print(clf.support_)
# 在每一个类中有多少个点属于支持向量
print(clf.n_support_) 
# 预测一个新的点
print(clf.predict([[2,0]]))

1.3.2  线性相关展示图案例

from sklearn import svm
import numpy as np
import matplotlib.pyplot as plt
 
np.random.seed(0)
x = np.r_[np.random.randn(20, 2) - [2, 2], np.random.randn(20, 2) + [2, 2]]  # 正态分布来产生数字,20行2列*2 
y = [0] * 20 + [1] * 20  # 20个class0，20个class1 
 
clf = svm.SVC(kernel='linear')
clf.fit(x, y)
 
w = clf.coef_[0]  # 获取w 
a = -w[0] / w[1]  # 斜率 
# 画图划线 
xx = np.linspace(-5, 5)  # (-5,5)之间x的值 
yy = a * xx - (clf.intercept_[0]) / w[1]  # xx带入y，截距 
 
# 画出与点相切的线 
b = clf.support_vectors_[0]
yy_down = a * xx + (b[1] - a * b[0])
b = clf.support_vectors_[-1]
yy_up = a * xx + (b[1] - a * b[0])
 
print("W:", w)
print("a:", a)
 
print("support_vectors_:", clf.support_vectors_)
print("clf.coef_:", clf.coef_)
 
plt.figure(figsize=(8, 4))
plt.plot(xx, yy)
plt.plot(xx, yy_down)
plt.plot(xx, yy_up)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1], s=80)
plt.scatter(x[:, 0], x[:, 1], c=y, cmap=plt.cm.Paired)  # [:，0]列切片，第0列 
 
plt.axis('tight')
 
plt.show() 

1.3.3 高斯核

1.

import numpy as np
import matplotlib.pyplot as plt
#准备数据
#x一维向量[-4 -3 -2 -1  0  1  2  3  4];y[0 0 1 1 1 1 1 0 0]
x=np.arange(-4,5,1)
print(x)
y=np.array((x>=-2)&(x<=2),dtype=int)
print(y)
plt.scatter(x[y==0],[0]*len(x[y==0]))
plt.scatter(x[y==1],[0]*len(x[y==1]))
plt.show()

2.

#定义高斯核函数
def guess(x,l):
    gamma=1.0
    return np.exp(-gamma*(x-l)**2)
#landmark
l1,l2=-1,1
#x_new,len(x)行，两列，第一列(np.exp(-gamma*(x-l1)**2)),第二列np.exp(-gamma*(x-l2)**2)
x_new=np.empty((len(x),2))
for i,data in enumerate(x):
    x_new[i,0]=guess(data,l1)
    x_new[i,1]=guess(data,l2)
plt.scatter(x_new[y==0,0],x_new[y==0,1])
plt.scatter(x_new[y==1,0],x_new[y==1,1])
plt.show()

3.

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
#使用管道将StandardScaler和SVC连在一起
from sklearn.pipeline import Pipeline
 
x,y=datasets.make_moons(noise=0.15,random_state=666)
print(x)
print(y)
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()
 
def RBFKernelSVC(gamma,C):
    return Pipeline([
        ('std_scaler',StandardScaler()),
        #采用高斯核函数rbf
        # gamma越大，高斯图形越窄，模型复杂度越高，容易导致过拟合
        # gamma越小，高斯图形越宽，模型复杂度越低，容易导致欠拟合
        ('svc',SVC(kernel='rbf',gamma=gamma,C=C))
    ])
 
svc1=RBFKernelSVC(0.1,1)
svc1.fit(x,y)
svc2=RBFKernelSVC(1,1)
svc2.fit(x,y)
svc3=RBFKernelSVC(10,1)
svc3.fit(x,y)
svc4=RBFKernelSVC(100,1)
svc4.fit(x,y)
 
svc5=RBFKernelSVC(0.1,5)
svc5.fit(x,y)
svc6=RBFKernelSVC(1,5)
svc6.fit(x,y)
svc7=RBFKernelSVC(10,5)
svc7.fit(x,y)
svc8=RBFKernelSVC(100,5)
svc8.fit(x,y)
def plot_decision_boundary(model,axis):
    x0,x1=np.meshgrid(
        np.linspace(axis[0],axis[1],int((axis[1]-axis[0])*100)),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100))
    )
    x_new=np.c_[x0.ravel(),x1.ravel()]
    y_predict=model.predict(x_new).reshape(x0.shape)
 
 
    from matplotlib.colors import ListedColormap
    # 自定义colormap
    custom_cmap=ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    plt.contourf(x0,x1,y_predict,linewidth=5,cmap=custom_cmap)
 
flg=plt.figure()
#flg.subplots_adjust(left=0.15,bottom=0.1,top=0.9,right=0.95,hspace=0.35,wspace=0.25)
plt.subplot(2, 4, 1), plt.title('gamma=0.1,C=1')
plot_decision_boundary(svc1,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4, 2), plt.title('gamma=1,C=1')
plot_decision_boundary(svc2,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4, 3), plt.title('gamma=10,C=1')
plot_decision_boundary(svc3,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4, 4), plt.title('gamma=100,C=1')
plot_decision_boundary(svc4,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4, 5), plt.title('gamma=0.1,C=5')
plot_decision_boundary(svc5,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4,6), plt.title('gamma=1,C=5')
plot_decision_boundary(svc6,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4, 7), plt.title('gamma=10,C=5')
plot_decision_boundary(svc7,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.subplot(2, 4, 8), plt.title('gamma=100,C=5')
plot_decision_boundary(svc8,axis=[-1.5,2.5,-1.0,1.5])
plt.scatter(x[y==0,0],x[y==0,1])
plt.scatter(x[y==1,0],x[y==1,1])
plt.show()

 

二.相关知识补充

1.拉格朗日乘子法

1.1 求解

得出：在相切点，圆的梯度向量和曲线的梯度向量平行。也就是梯度向量平行，用数学符号表示为：。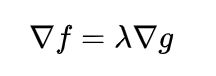

引入条件，否则这么多等高线，不知道指的具体是哪一根。

联立方程：

求出：

 

1.2 定义

要求函数 在 约束下的极值这种问题可以表示为：

 （ 意思是subject to，服从于，约束于的意思）

列出方程组进行求解：

例：

1.3 变形

（把等式左边的偏导算出来就和上面的定义是一样的了）

3.4 多个约束条件

例：

约束条件如图：

所求的距离如图：

 

则：

 

2.对偶问题（KKT条件）

1.

2.例子：

 

 3.核函数（高斯核）

 1.介绍

高斯核函数是SVM中使用最多的一种核函数，对比高斯函数x-u,高斯核函数中表征的是两个向量(x,y)之间的关系，高斯函数又被称为RBF核和径向基核函数。在多项式核函数中，我们知道多项式核函数是将数据点添加多项式项，再将这些有了多项式项的特征点进行点乘，就形成了多项式核函数，对于高斯核函数也是一样，首先将原来的数据点映射成一种新的特征向量，然后得到新的特征向量点乘的结果，对高斯核函数来说，本质就是将每一个样本点映射到一个无穷维的特征空间，这就表明高斯核函数对于样本数据的变形是非常复杂的，但是经过变形，再去点乘，得到的结果却是非常简明的，就是核函数中的式子，这样也表明了核函数的威力。
 

 为了方便可视化，对核函数进行改变，对于y值不取样本点，取固定的值，取两个固定的点l1,l2（landmark）。高斯核函数对于一维数据升维成二维点，这样我们就将一维的样本点映射到了二维空间，具体取值下图所示，并通过程序模拟是怎样通过这样一个高斯核函数将一维线性不可分的数据变得线性可分的。

 

 

 

 

相关资料原文：

SVM：原文链接：https://blog.csdn.net/qq_31347869/article/details/88071930
拉格朗日乘子法：原文链接：https://blog.csdn.net/ccnt_2012/article/details/81326626

KKT条件：https://zhuanlan.zhihu.com/p/38163970