cs224w-图机器学习-2021冬课程学习笔记-5- Message Passing and Node Classification
Message Passing and Node Classification
- 一、分类背后的直觉
-
- 1.分类问题的表述
- 2.本章内容大纲
- 3.Correlations
-
- (1)Homophily
- (2)Influence
- 4.如何利用Correlations来进行预测
- 5.分类器的主要组成
- 二、Relational classification
- 三、Iterative classification
-
- 1.两个分类器
- 2.迭代过程
- 3.例子
- 4.本节小结
- 四、Loopy belief propagation
-
- 1.解释什么是belief propagation
- 2.belief propagation形式化说明(没懂,未看。需回炉重造)
一、分类背后的直觉
1.分类问题的表述
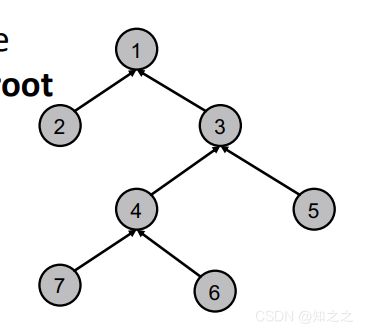
根据一部分带标签的节点数据,预测新节点的标签。
如预测下图中灰色节点类型:
2.本章内容大纲
使用message passing的方法分类。其背后的直觉是:Correlations exist in networks。即相似的节点是相连的。
将会讨论三种技术:

这些都是古老的技术,但是给图神经网络提供了很多intuition。这相当于是GNN的前奏。
3.Correlations
内涵就是:相近的节点,其标签相似(可不可以理解为“物以类聚人以群分?”)。各个节点之间的行为是相关的
为什么会有这种Correlations?这里给出了两个原因:
即
Homophily和Influence
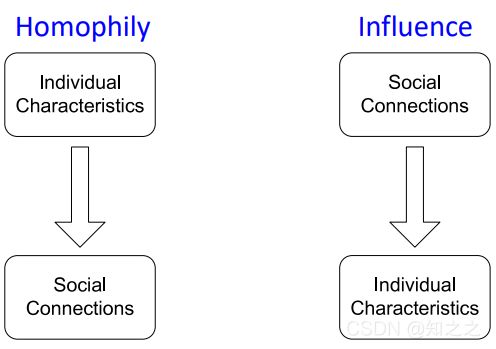
(1)Homophily
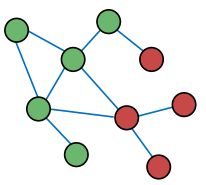
指的是相似的人之间更容易有联系。(The tendency of individuals to associate and bond with similar others)。如两个研究ML的学者,他们容易互相认识(比如参加同一个会议);其他方面如年龄、爱好等各个方面,都表现出这个特征。一个例子:

可以看出上图大致分为四组人,每一组人有不同的爱好(如运动、艺术方面的)。
(2)Influence
正好和上面的Homophily相反。这指的是:社会关系能影响一个人的特性(Social connections can influence the individual characteristics of a person.)如我的朋友给我推荐歌曲、游戏。
4.如何利用Correlations来进行预测
- “连坐制”Guilt-by-association:和X相连的节点是啥,X就倾向于是啥。比如恶意网页互相链接。因此如果发现X网站和恶意网站有链接,那么X也很可能是恶意网站。(感觉这个很实用,与现实还是挺相符的。LOL可能就在用这个机制匹配队友。如果X老是挂机,那么他匹配到的人,也超级爱挂机,三分钟的概率贼高)
- 根据邻居和自己的特征分类:节点v的标签取决于v的特征,和邻居的特征、标签。
用这些intuition进行自监督学习,其引入的归纳偏好就是,网络中存在某种程度的Homophily。
5.分类器的主要组成
算法是一种Probabilistic framework。
分类器包括三个步骤:
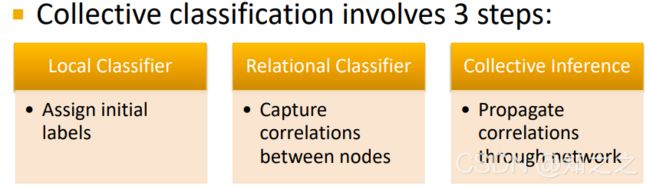
这个算法使用了这个假设:Markov Assumption:即节点的标签取决于其一阶邻居的标签:
![]()
其中三个部分作用分别是:(后面会讲具体实现,先不写了)

Local Classfier得名应该源自于,这分类器只使用了节点特征信息,而没有用到图的结构信息。因此称为Local。
二、Relational classification
方法描述:每个节点的标签是其一阶邻居的标签的概率的加权平均,然后迭代此步骤。表述如下:

其中 A v , u A_{v,u} Av,u是邻接矩阵或者权值的邻接矩阵。
这个方法有俩问题:
- 不保证收敛性
- 不能利用节点的特征信息。
例子如下:
首先对灰色节点初始化概率,设置为0.5

然后按照一定的顺序迭代:


最终结果(收敛了):

三、Iterative classification
1.两个分类器
本方法使用了节点的特征信息。具体过程是,训练两个分类器:

ϕ 1 ( f v ) \phi_{1}(f_{v}) ϕ1(fv)只使用节点的特征数据做分类,然后 ϕ 2 ( f v , z v ) \phi_{2}(f_{v},z_{v}) ϕ2(fv,zv)使用节点特征信息和一个summary向量 z v z_{v} zv做分类。其中 z v z_{v} zv是邻居节点的标签的汇总向量,有很多种选择,比如每一项对应着邻居节点中某个类出现的比例。下图中, z v = [ 0.66 , 0.33 ] ⊤ z_{v}=[0.66,0.33]\top zv=[0.66,0.33]⊤

2.迭代过程
-
第一阶段
在训练集上,训练 ϕ 1 ( f v ) \phi_{1}(f_{v}) ϕ1(fv)和 ϕ 2 ( f v , z v ) \phi_{2}(f_{v},z_{v}) ϕ2(fv,zv)

3.例子
根据Web的关键词、网页间互相链接的关系,预测一个Web的主题。
最简单的方式就是根据Web 的关键词(即节点特征)直接预测。但是这就没有用上链接的关系:如果已知其互相链接的Web的主题,那么这些数据也可以用来预测本Web的主题。
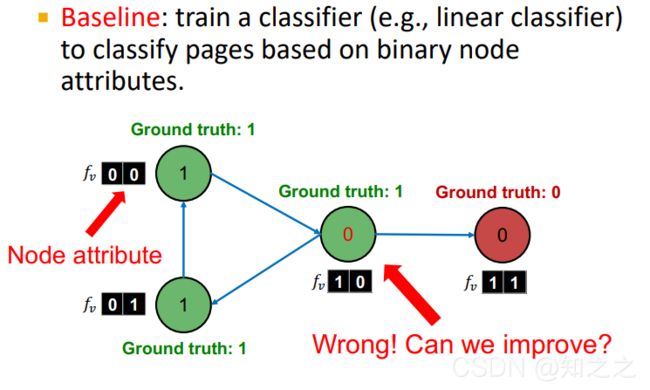
问题描述:

Baseline:只用节点属性(features)的分类器。这个分类器将中间的节点分错了:本应该是绿色标签为1,预测成了0。这分类器可以想象成根据attribute的第一个分量进行预测的。
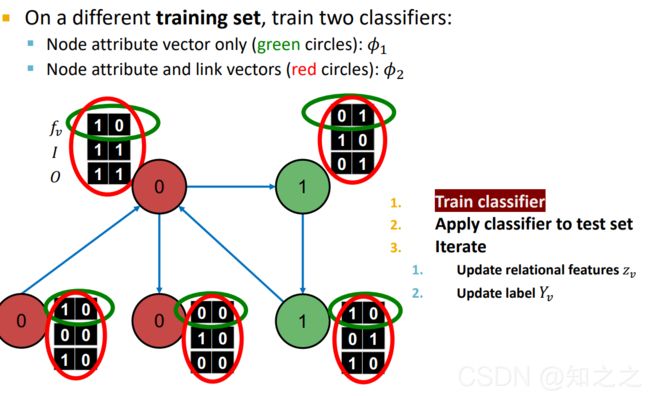
加上 z v z_{v} zv后,特征变多了:一个 z v z_{v} zv四个分量,分别是出边和入边。其中第一个分量指示是否指向的是0类节点:

准备工作做好了。现在开始训练模型:
- 第一步,在训练集上训练两个分类器:
- 用训练好的分类器,给未标注的节点分配一个标签:(可以看出,中间的节点分类错误了。但是后面的迭代能把这个错误纠正。这就是用了图的连边信息的作用)

- 迭代。
(1). 根据上一步分配好的初始化标签,更新每个节点的z向量:
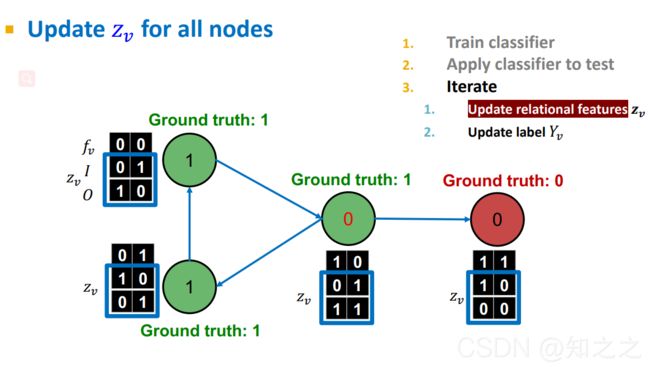
(2).根据更新后的z向量,用分类器2更新每个节点的标签:

当停止迭代后,结果如下:
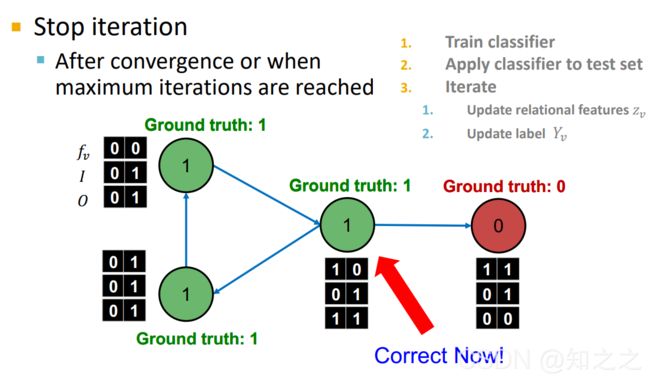
可以看出,通过这两个分类器配合迭代,把中间的节点分类正确了。
4.本节小结
本节和上个小节讲了两种collective classification的方法。前者只用了邻居信息没有用到节点的特征;后者利用了节点特征进行更新迭代,完成分类。

四、Loopy belief propagation
1.解释什么是belief propagation
也是用于collective classification
这个还是有点难的,参考这里
例子:
有这么一个链式网络,现在要数这个网络有几个节点(通过节点之间的一次次传递消息,实现让每个节点都知道网络中有多少节点)。规定只能从右往左传递消息。

1号节点知道自己右边没有节点,因此他知道只有自己一个人,因此传递消息1送给2。然后节点2把节点1传来的数据加上1(自己)传给3,以此类推。

这个过程很有种,根据局部推全局的意思:每个节点都知道局部的一点信息,然后大家都更新一下信息,就有了全局的解。(果然是动态规划算法)
下面是树形数据进行传播: