[StudyNote]Neural Networks&Deep Learning--Andrew Ng【待续】

[email protected]

week 1

1.1 Standard NN

x1 x2 x3 x4为输入特征，已知影响房价的特征，神经网络要做的工作为预测对应房屋价格。
圆圈的为隐藏单元，每个输入都同时来自于4个特征，然后由神经网络自己决定用哪几个特征进行计算。
故只要给神经网络喂足大量数据，习得一个函数，就能计算从x->y的精准映射函数。即监督学习（supervised learning）

week 2

2.1 符号简介

pic 像素为aXa转化为aXa矩阵，每个元素为RGB的亮度，用特征x接收矩阵，nx/n表示向量的维度aa3

图1 符号介绍

（x,y）表示一个样本，m为样本容量，所有样本组成X矩阵

2.2 Logistic Regression-----浅层模型

单个样本的logistic：

图1 单个样本的logistic回归公式

w、b是我们需要学习的参数
y是样本的ground truth lable(基本真值标签)
a是logistics回归的输出，即预测值

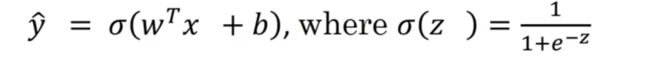
sigmoid函数

图2 y—hat公式

Logistic Regression是用在监督学习的一个学习算法，输出y hat标签为0或者1，是个二元分类问题

y hat ->possibility

因为output y hat可能不在0-1之间，故用Simoid(z)将y hat 取值介于01之间
我们要做的是学习参数w和b

图3 y-hat 作用图解

图4 z的大小与y hat 取值对应关系

2.2.1 loss function-----衡量单个训练集上表现

Loss function 衡量预测输出值y hat 与y实际值多接近
类似于误差平方的作用，解决一些凸的优化问题

类似于平方差，y 与y hat 尽可能接近，故损失函数取值尽可能小，根据Loss Func & y hat 处在[0,1],以下讨论两种情况：

2.2.2 cost function-----衡量全体训练集上表现

Cost Function:J(w,b) 对样本总量m的Loss求值

图1 cost Func 公式

2.2.3 P

定义式为，其实加完log就是cost function 的负值形式
因为cost最小化，log->p最大化

2.3 Derivatives with a Computation Graph

图1 反向传播

dvar-> FinalFinfOutVar
理解成dvar变化量与InputVar变化量的比值

2.4 gradient descent algorithm(梯度下降法)----学习训练w、b

2.4.1 单个训练集

基于2.1的3个公式，计算两个特征x1 x2的情况

根据链式法则，反向求导计算出dL与各变量的比值
通过导数来修改w1 w2 b 的值以最小化损失函数

优化参数

梯度下降法，重复求导过程，通过改变w1 w2 b实现dvar 的最小化

2.4.2 全体训练集

2.5 Vectorization（向量化）

取代for语句，提高训练速度

2.5.1正向传播

1.同时计算整个训练集 Z
（n，m）的X矩阵为xi的向量化，Python语法中的broadcasting将实数b直接转化为（1，m）的矩阵，一起计算出整个训练集的Z

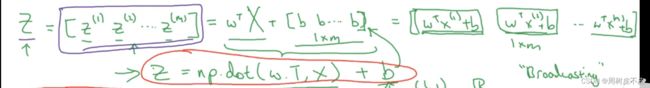
2.A

2.5.2 反向传播

1.dZ=A-Y
2.dw
即对 X中的xi求变化量/m
首行为python代码

3. db

2.5.3 综合应用

综上，可将原代码中的for用向量化替换（右）
若需要进行迭代求导再考虑用for

week 3 单隐层神经网络

3.1 神经网络介绍

单隐层神经网络

0：输入层
1：隐藏层

2：输出层

根据矩阵知识，横向对应不同训练集，纵向对应单个训练集中不同隐藏层的激活函数

3.2 激活函数

1.sigmoid

求导情况之前也有

2.tanh


3.ReLU修正限行函数（开局房价）
g(z)=max(0,z)

小于0为0 0处未定义 大于0处导数为1
让所有yhat都大于0，有点像复变里的筛选？

还有一种带泄漏的ReLU激活函数
g(z)=(0.01z,z)

4.linear activation function/indentity activation function(线性激活函数/恒等激活函数）
输出直接是输入的线性组合
即原来y—hat的sigmoid（z）直接变z=g（z）

会发现最后输出为kx+b形式，所以隐藏层中用多次也是线性，没意义，只有在输出层ok。andrew还说机器学习回归用，不了解

3.3 反向传播—gradient descent algorithm

自己感觉跟之前的logistic差不多8

3.4 随机初始化

保证使用不同的隐藏单元计算不同函数，w，b倒是无所谓
*的系数尽量小，保证w小，使激活函数sigmoid tanh落在比较陡的区域，梯度下降学习起来更快

week 4