【控制】基于灰狼算法改进分数阶PD滑模控制器附matlab代码

1 内容介绍

分数微积分已经被研究了将近 3 个世纪，并且已 经被科学家广泛应用到科学与控制工程领域中。分 数阶 PID 控制系统是由斯洛伐克学者 Podlubny于 1994 年提出，并应用于分数阶模糊系统中。在此项工 作之后，其他的工程师应用不同的设计与调整方法设 计出分数阶 PID 控制器。分数阶微积分为复杂成比例 的系统过程和事件提供完善的数学模型，应用于物理、 生物与控制理论方面。 分数模糊控制器( FFCs) 是传统模糊控制器与分 数阶算子结合，在多种动力系统中表现出比传统的模 糊控制器更好的性能。分数阶模糊控制器中的参数估 计问题一般用进化算法去优化求解，提高控制器的精 度与稳定性能。例如: 用遗传算法模糊分数阶控制器 模型问题; 用混沌粒子群算法对可再生发电混合动 力系统进行分数阶模糊控制器; 使用微分和声搜索 算法设计分数阶; 采用改进的重力搜索算法对抽水 蓄能水电机组进行快速模糊分数阶 PID 控制; 分数阶模糊 PID 控制器在机械手臂中的应用性能分析; 社会蜘蛛群算法对分数模糊控制器参数标定。虽然这些算法都获得比较理想的结果，但是仍然具有一 个很重要的局限性，由于其搜索策略中的勘探与开采 之间的平衡关系，容易陷入局部最优的解，这种行为会 导致整个种群快速集中在最优粒子周围，容易形成早 熟收敛，不利于搜索空间的探索。 灰狼优化算法是由 Mirjalili 等于 2014 年提出 的新型群智能优化算法。灰狼优化算法( GWO) 是模 拟灰狼的狩猎机制，包括搜索猎物、追踪猎物、包围猎 物与捕杀猎物等步骤，与其他的元启发式优化算法不 同，该算法考虑领导阶层。由于该算法具有较好的平 衡勘探与开采能力，所以该算法越来越受到相关领域 的人们重视，并成功地应用于一些实际工程问题中。

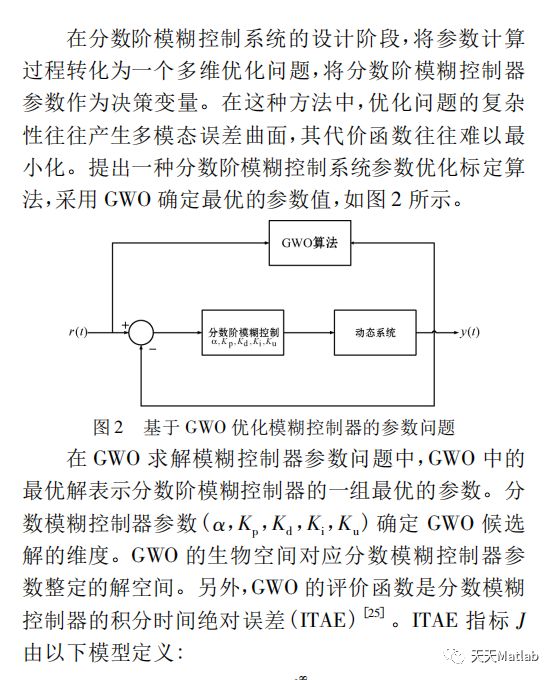
PID模糊控制在工业控制中是最广泛的一种控制方法,在一些复杂的实际系统中,应用分数阶PID模糊控制器在整定系统参数性能上优于整数模糊控制器.分数阶模糊控制器具有较多的控制参数,这些控制参数直接影响了模糊控制器的性能.用传统的算法校准分数阶模糊控制器并不能得到最佳的参数值,而且标定参数的过程较为复杂.因此提出用灰狼优化算法(Grey Wolf Optimizer,GWO)优化分数阶模糊控制器的参数.将基于灰狼优化算法的分数阶模糊控制器优化方法与其他五种典型的基于群智能的优化方法进行了比较.实验结果表明,该方法的控制效果更好.

2 仿真代码

​​% Grey Wolf Optimizerfunction [Alpha_score,Alpha_pos,Convergence_curve]=GWOr(SearchAgents_no,Max_iter,lb,ub,dim)x0=[-pi pi 0 0 0 0];Ts=[0 5]; % initialize alpha, beta, and delta_posAlpha_pos=zeros(1,dim);Alpha_score=inf; %change this to -inf for maximization problems​Beta_pos=zeros(1,dim);Beta_score=inf; %change this to -inf for maximization problems​Delta_pos=zeros(1,dim);Delta_score=inf; %change this to -inf for maximization problems​%Initialize the positions of search agentsPositions=initializationr(SearchAgents_no,dim,ub,lb);​Convergence_curve=zeros(1,Max_iter);​l=0;% Loop counter​% Main loopwhile l    l    for i=1:size(Positions,1)                         % Return back the search agents that go beyond the boundaries of the search space%         Flag4ub=Positions(i,:)>ub;%         Flag4lb=Positions(i,:)%         Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;           Kpd=Positions(i,:);        [T,X] = ode45(@(t,x) r2dof(t,x,Kpd),Ts,x0);​        qd1=sin(4.17*T);        % qdot_r1=4.17*cos(4.17*T);        % qdot2_r1=-4.17*4.17*sin(4.17*T);        qd2=1.2*sin(5.11*T);        % qdot_r2=1.2*5.11*cos(5.11*T);        % qdot2_r2=-1.2*5.11*5.11*sin(5.11*T);​        th1=X(:,1); %theta1 wavwform        th2=X(:,2);        fitness=Fitnessr(th1,th2,qd1,qd2);        % Calculate objective function for each search agent%         fitness=Fitnessr(Positions(i,:));                % Update Alpha, Beta, and Delta        if fitness            Alpha_score=fitness; % Update alpha            Alpha_pos=Positions(i,:);        end                if fitness>Alpha_score && fitness            Beta_score=fitness; % Update beta            Beta_pos=Positions(i,:);        end                if fitness>Alpha_score && fitness>Beta_score && fitness            Delta_score=fitness; % Update delta            Delta_pos=Positions(i,:);        end    end            a=2-l*((2)/Max_iter); % a decreases linearly fron 2 to 0        % Update the Position of search agents including omegas    for i=1:size(Positions,1)                %         for j=1:size(Positions,2)                                        r1=rand(); % r1 is a random number in [0,1]            r2=rand(); % r2 is a random number in [0,1]                        A1=2*a*r1-a; % Equation (3.3)            C1=2*r2; % Equation (3.4)                        D_alpha=abs(C1*Alpha_pos-Positions(i,:)); % Equation (3.5)-part 1            X1=Alpha_pos-A1*D_alpha; % Equation (3.6)-part 1                                   r1=rand();            r2=rand();                        A2=2*a*r1-a; % Equation (3.3)            C2=2*r2; % Equation (3.4)                        D_beta=abs(C2*Beta_pos-Positions(i,:)); % Equation (3.5)-part 2            X2=Beta_pos-A2*D_beta; % Equation (3.6)-part 2                               r1=rand();            r2=rand();                         A3=2*a*r1-a; % Equation (3.3)            C3=2*r2; % Equation (3.4)                        D_delta=abs(C3*Delta_pos-Positions(i,:)); % Equation (3.5)-part 3            X3=Delta_pos-A3*D_delta; % Equation (3.5)-part 3                                     Positions(i,:)=(X1+X2+X3)/3;% Equation (3.7)            %         end    end    l=l+1;        Convergence_curve(l)=Alpha_score;end​​​​

3 运行结果

4 参考文献

[1]范鲁娜. 灰狼算法优化分数阶模糊控制器参数[J]. 计算机应用与软件, 2021, 38(10):6.

[1]阎晓妹, 尚婷, 赵小国. 基于分数阶滑模控制器的不确定分数阶混沌系统同步[J]. 应用数学学报, 2018, 41(6):12.

博主简介：擅长智能优化算法、神经网络预测、信号处理、元胞自动机、图像处理、路径规划、无人机等多种领域的Matlab仿真，相关matlab代码问题可私信交流。

部分理论引用网络文献，若有侵权联系博主删除。