[机器学习导论]——第三课——神经网络Ⅱ
文章目录
- 第三课——神经网络Ⅱ
-
- 反向传播的一般情形
-
- 反向传播方程
- 反向传播算法
- 神经网络模型参数求解步骤
- mini-batch
- 方程证明
-
- BP1的证明
- BP2的证明
- BP3的证明
- BP4的证明
- 神经网络模型改进
-
- 改进损失函数:对数似然
-
- 示例
- 反向传播方程
- 权重初始化
- 减少过拟合:dropout
- 缓解梯度消失:ReLU
-
- 梯度消失问题
- 使用ReLU进行缓解
- 参考资料
第三课——神经网络Ⅱ
机器学习与神经网络
多层感知器(MLP,MultilayerPerceptron)是一种前馈人工神经网络模型,其将输入的多个数据集映射到单一的输出的数据集上。
反向传播的一般情形
第层第个神经元和第−1层神经元之间关系
k是上一层神经元的坐标
在第层第个神经元的误差如下:
δ j l ≡ ∂ E ∂ z j l \delta_j^l\equiv \frac{\partial E }{\partial z_j^l} δjl≡∂zjl∂E
反向传播方程
四个反向传播方程如下:
第一个反向传播方程是在计算输出层的误差
第二个反向传播方程是用L层的误差推导L-1层的误差,建立了两层之间的递推关系
第三个反向传播方程是损失函数关于任意一层偏差b的导数
第四个反向传播方程是损失函数关于任意一层权重W的导数
反向传播算法
1️⃣输入:为输入层设置对应的激活值ℎ1
2️⃣前向传播:∀=2,…,,计算 z l = ( W l − 1 ) T h l − 1 + b l − 1 和 h l = σ ( z l ) z^l=(W^{l-1})^Th^{l-1}+b^{l-1}和h^l=\sigma(z^l) zl=(Wl−1)Thl−1+bl−1和hl=σ(zl)
3️⃣输出层误差 δ L \delta^L δL和反向误差传播 δ l ( l = L − 1 , … , 2 ) \delta^l(l=L−1,…,2) δl(l=L−1,…,2):(BP1)和(BP2)
4️⃣输出:误差函数的梯度由(BP3)和(BP4)给出
神经网络模型参数求解步骤
遍历所有数据算一次损失函数,然后计算梯度,更新梯度。每更新一次都需要将数据集中的所有样本遍历一遍,计算量大
E = 1 2 n ∑ x ∣ ∣ y x − h x , L ∣ ∣ 2 E=\frac{1}{2n}\sum_x||y^x-h^{x,L}||^2 E=2n1x∑∣∣yx−hx,L∣∣2
1️⃣输入训练样本 { x i , i = 1 , . . . , n } \{x_i,i=1,...,n\} {xi,i=1,...,n}的集合
2️⃣对每个训练样本x:设置对应的激活值 h x , 1 h^{x,1} hx,1
1️⃣前向传播:∀=2,…,,计算 z x , l = ( W l − 1 ) T h x , l − 1 + b x , l − 1 和 h x , l = σ ( z x , l ) z^{x,l}=(W^{l-1})^Th^{x,l-1}+b^{x,l-1}和h^{x,l}=\sigma(z^{x,l)} zx,l=(Wl−1)Thx,l−1+bx,l−1和hx,l=σ(zx,l)
2️⃣输出层误差 δ x , L = ( h x , L − y x ) ⊙ σ ′ ( z x , L ) \delta^{x,L}=(h^{x,L}-y^x)\odot\sigma'(z^{x,L}) δx,L=(hx,L−yx)⊙σ′(zx,L)
3️⃣反向传播误差 δ x , l ( l = L − 1 , . . . , 2 ) = σ ′ ( z x , l ) ⊙ ( W l δ x , l + 1 ) \delta^{x,l}(l=L-1,...,2)=\sigma'(z^{x,l})\odot(W^l\delta^{x,l+1}) δx,l(l=L−1,...,2)=σ′(zx,l)⊙(Wlδx,l+1)
3️⃣梯度下降:对每个 l = L − 1 , . . . , 2 l=L-1,...,2 l=L−1,...,2
W l − 1 → W l − 1 − η n ∑ x h x , l − 1 ( δ x , l ) T b l − 1 → b l − 1 − η n ∑ x δ x , l \ W^{l-1}\rightarrow W^{l-1}-\frac{\eta}{n}\sum_x h^{x,l-1}(\delta^{x,l})^T\\ b^{l-1}\rightarrow b^{l-1}-\frac{\eta}{n}\sum_x \delta^{x,l} Wl−1→Wl−1−nηx∑hx,l−1(δx,l)Tbl−1→bl−1−nηx∑δx,l
4️⃣重复步骤2中的(1-3)和步骤3,直至收敛。
mini-batch
将数据分为若干个批,按照批次来更新参数,这样一个批中的一组数据共同决定了本次梯度的方向,计算量也少了许多
1️⃣输入训练样本 { x i , i = 1 , . . . , n } \{x_i,i=1,...,n\} {xi,i=1,...,n}的集合
2️⃣Fori=1:n/m
3️⃣对批量数据中的每个训练样本x:设置对应的激活值 h x , 1 h^{x,1} hx,1
1️⃣前向传播:∀=2,…,,计算 z x , l = ( W l − 1 ) T h x , l − 1 + b x , l − 1 和 h x , l = σ ( z x , l ) z^{x,l}=(W^{l-1})^Th^{x,l-1}+b^{x,l-1}和h^{x,l}=\sigma(z^{x,l)} zx,l=(Wl−1)Thx,l−1+bx,l−1和hx,l=σ(zx,l)
2️⃣输出层误差 δ x , L = ( h x , L − y x ) ⊙ σ ′ ( z x , L ) \delta^{x,L}=(h^{x,L}-y^x)\odot\sigma'(z^{x,L}) δx,L=(hx,L−yx)⊙σ′(zx,L)
3️⃣反向传播误差 δ x , l ( l = L − 1 , . . . , 2 ) = σ ′ ( z x , l ) ⊙ ( W l δ x , l + 1 ) \delta^{x,l}(l=L-1,...,2)=\sigma'(z^{x,l})\odot(W^l\delta^{x,l+1}) δx,l(l=L−1,...,2)=σ′(zx,l)⊙(Wlδx,l+1)
4️⃣梯度下降:对每个 l = L − 1 , . . . , 2 l=L-1,...,2 l=L−1,...,2
W l − 1 → W l − 1 − η m ∑ x h x , l − 1 ( δ x , l ) T b l − 1 → b l − 1 − η m ∑ x δ x , l \ W^{l-1}\rightarrow W^{l-1}-\frac{\eta}{m}\sum_x h^{x,l-1}(\delta^{x,l})^T\\ b^{l-1}\rightarrow b^{l-1}-\frac{\eta}{m}\sum_x \delta^{x,l} Wl−1→Wl−1−mηx∑hx,l−1(δx,l)Tbl−1→bl−1−mηx∑δx,l
5️⃣Endi(一个epoch,迭代期)
6️⃣进行多个epoch循环,直至收敛重复步骤2中的(1-3)和步骤3,直至收敛。
首先,如果训练集较小,直接使用batch梯度下降法,样本集较小就没必要使用minibatch梯度下降法,你可以快速处理整个训练集,所以使用batch梯度下降法也很好,这里的少是说小于2000个样本,这样比较适合使用batch梯度下降法。不然,样本数目较大的话,一般的mini-batch大小为64到512,考虑到电脑内存设置和使用的方式,如果minibatch大小是2的次方,代码会运行地快一些,64就是2的6次方,以此类推,128是2的7次方,256是2的8次方,512是2的9次方。所以我经常把mini-batch大小设成2的次方。在上一个视频里,我的mini-batch大小设为了1000,建议可以试一下1024,也就是2的10次方。也有mini-batch的大小为1024,不过比较少见,64到512的mini-batch比较常见。
方程证明
BP1的证明
粗略证明
对每个元素来看
第层第个神经元和第−1层神经元之间的关系:
中间变量 δ j l ≡ ∂ E ∂ z j l \delta^l_j\equiv\frac{\partial E}{\partial z^l_j} δjl≡∂zjl∂E,称为在第层第个神经元的误差。
输出层误差的方程, δ j L ( B P 1 ) \delta^L_j(BP1) δjL(BP1):
输出层误差的向量表达形式, δ L ( B P 1 ) \delta^L(BP1) δL(BP1)
δ L = ( h L − y ) ⊙ σ ′ ( z L ) \delta^L=(h^L-y)\odot\sigma'(z^L) δL=(hL−y)⊙σ′(zL)
BP2的证明
使用下一层的误差 δ l + 1 \delta^{l+1} δl+1表示当前层误差Font metrics not found for font: .
δ l = σ ′ ( z l ) ⊙ ( W l δ l + 1 ) \delta^l=\sigma'(z^l)\odot(W^l\delta^{l+1}) δl=σ′(zl)⊙(Wlδl+1)
![[机器学习导论]——第三课——神经网络Ⅱ_第9张图片](http://img.e-com-net.com/image/info8/1df22294c0af44399bc6b121d8c56dd2.jpg)
BP3的证明
代价函数关于偏置的偏导 ∂ E ∂ b l − 1 ( B P 3 ) \frac{\partial E}{\partial b^{l-1}}(BP3) ∂bl−1∂E(BP3):
∂ E ∂ b l − 1 ( B P 3 ) = δ l \frac{\partial E}{\partial b^{l-1}}(BP3)=\delta^l ∂bl−1∂E(BP3)=δl
![[机器学习导论]——第三课——神经网络Ⅱ_第11张图片](http://img.e-com-net.com/image/info8/7eebade20c7a440aacd705c0998eaaf0.jpg)
BP4的证明
代价函数关于权重的偏导KaTeX parse error: Undefined control sequence: \partialE at position 7: \frac{\̲p̲a̲r̲t̲i̲a̲l̲E̲}{\partialW_{jk…:
∂ E ∂ W j k l − 1 = h k l − 1 δ j l ∂ E ∂ W l − 1 = h l − 1 ( δ l ) T \frac{\partial E}{\partial W_{jk}^{l-1}}=h^{l-1}_k\delta^l_j\\ \frac{\partial E}{\partial W^{l-1}}=h^{l-1}(\delta^l)^T ∂Wjkl−1∂E=hkl−1δjl∂Wl−1∂E=hl−1(δl)T
![[机器学习导论]——第三课——神经网络Ⅱ_第12张图片](http://img.e-com-net.com/image/info8/aff5923d0ef74fbea6243f9a1ce19e46.jpg)
(2022/3/10)
神经网络模型改进
改进损失函数:对数似然
以逻辑回归为例
| 二次代价 | 交叉熵 | |
|---|---|---|
| 损失函数 | 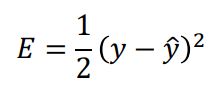 |
|
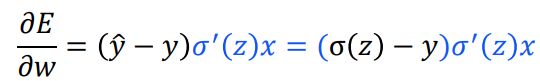 |
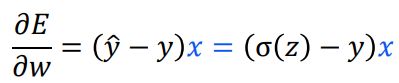 |
|
 |
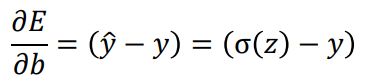 |
示例
任务:让输入1转化为0
1️⃣二次代价:初始权重和偏置设置为2.0,此时初始输出为0.98,学习率为0.15
刚开始学习的速度比较缓慢,对于前150左右的学习次数,权重和偏置没有发生太大变化。随后当预测输出值远离1时,学习速度加快。
注意到
σ ′ ( z ) = σ ( z ) ( 1 − σ ( z ) ) \sigma'(z)=\sigma(z)(1-\sigma(z)) σ′(z)=σ(z)(1−σ(z))因此,当预测输出接近1的时候’()很小,导致梯度很小,因而学习缓慢。当预测输出远离1时,学习速度加快。]
2️⃣交叉熵代价:初始权重和偏置设置为2.0,此时初始输出为0.98,学习率为0.005
刚开始学习的速度相当快,与期待一样,当严重错误时能以最快速度学习;当预测输出接近正确输出时,学习速度变慢,也符合预期。
通过梯度公式可以看出,当预测输出与实际输出之间的差异越大时,梯度越大,因此学习速度也更快,相反当二者之间的差异较小时,学习速度变慢。因此交叉代价函数在分类问题应用更加广泛。
反向传播方程
以包含两个隐藏层的三分问题为例,假设样本属于第二类i=2,使用softmax函数代替sigmoid函数
权重初始化
随机初始化:使用Numpy的 np.random.randn函数生成均值为0,标准差为1的高斯分布
对于第一个隐层的神经元
若假设有一半的 h k 1 = 1 h_k^1=1 hk1=1,另一半为0,则 z j 2 z_j^2 zj2服从均值为0,标准差为 p 2 + 1 \sqrt{\frac{p}{2}+1} 2p+1的高斯分布
σ ( z j 2 ) \sigma(z_j^2) σ(zj2)接近于1或0,梯度很小,导致学习速度很慢
**改进 **:对于任意层,使用均值为0,标准差为 1 n i n + 1 \frac{1}{\sqrt{n_{in}+1}} nin+11的高斯分布随机分布初始化权重参数 W l − 1 , b l − 1 W^{l-1},b^{l-1} Wl−1,bl−1。此时中间变量 z j l z_j^l zjl服从均值为0,标准差为1的高斯分布:
大部分神经元的值 σ ( z j l ) \sigma(z_j^l) σ(zjl)离0或1较远,从而学习速度快
减少过拟合:dropout
随机地删除网络中的一半的隐藏神经元,同时让输入层和输出层的神经元保持不变
把输入x通过修改后的网络前向传播,然后把得到的损失结果通过修改的网络反向传播。在mini-batch 上执行完这个过程后,在没有被删除的神经元上更新对应的参数(w,b)
Dropout
1️⃣ 继续重复上述过程
2️⃣ 恢复被删掉的神经元(此时被删除的神经元保持原样,而没有被删除的神经元已经有所更新)
3️⃣ 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉(备份被删除神经元的参数)。
4️⃣ 对一小批训练样本,先前向传播然后反向传播损失并更新参数(w,b)(没有被删除的那一部分参数得到更新,删除的神经元参数保持被删除前的结果)。
缓解梯度消失:ReLU
梯度消失问题
对于特定的分类问题,神经网络不是层数越多越好。
假设每层的神经元个数都为1,则
若 | |小于1,则当层数很多以后,容易导致梯度消失
使用ReLU进行缓解
ReLU激活函数
当是负数的时候,梯度为0,神经元停止学习(类似于 dropout作用,减少过拟合);当大于0时,梯度为1,可 以缓解下溢问题
参考资料
[1]庞善民.西安交通大学机器学习导论2022春PPT
[2]周志华.机器学习.北京:清华大学出版社,2016
[3]MichaelA.Nielsen,“NeuralNetworksandDeepLearning”,DeterminationPress,2015
[4]2-2理解mini-batch梯度下降法
![[机器学习导论]——第三课——神经网络Ⅱ_第1张图片](http://img.e-com-net.com/image/info8/cb0dcce9273c47058da06098bae7cea9.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第2张图片](http://img.e-com-net.com/image/info8/068f092a47d34f57bc8c06a599c82d33.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第3张图片](http://img.e-com-net.com/image/info8/57cba32c79d647ca9f8e308d0a115e9d.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第4张图片](http://img.e-com-net.com/image/info8/c9d6656052944e4e95cc0136fc4074e3.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第5张图片](http://img.e-com-net.com/image/info8/776bfdd79ab84eaf846b9465aed0c8f0.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第6张图片](http://img.e-com-net.com/image/info8/2e31e3b0f77b483eb549c5eae121d40f.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第7张图片](http://img.e-com-net.com/image/info8/e25d9655b6a3418b9a953f4c6afe0aad.jpg)

![[机器学习导论]——第三课——神经网络Ⅱ_第8张图片](http://img.e-com-net.com/image/info8/823d0724ba1a4bb685c04d1a672e20af.jpg)
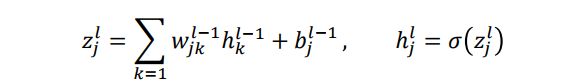
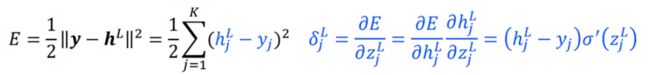
![[机器学习导论]——第三课——神经网络Ⅱ_第10张图片](http://img.e-com-net.com/image/info8/6876c6e5e6d74b738a3f62a5cb0cc6b6.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第13张图片](http://img.e-com-net.com/image/info8/b944bf8e2cfc4b83a7373bd3928a190f.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第14张图片](http://img.e-com-net.com/image/info8/85ffba621df447c7b543c48878f8ebe2.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第15张图片](http://img.e-com-net.com/image/info8/d2de5092889344bab24ecf64962f7055.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第16张图片](http://img.e-com-net.com/image/info8/f8c146185ef7430190be237ea6b855fe.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第17张图片](http://img.e-com-net.com/image/info8/f1ea441c29914992b05f660c7be86604.jpg)
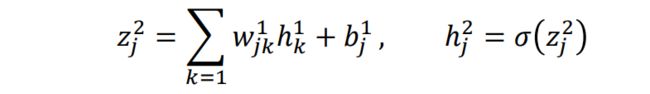
![[机器学习导论]——第三课——神经网络Ⅱ_第18张图片](http://img.e-com-net.com/image/info8/c6262b1e9901473a91027a2a2df2b056.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第19张图片](http://img.e-com-net.com/image/info8/595de064384842e98c34fccc6bfb30dd.jpg)
![[机器学习导论]——第三课——神经网络Ⅱ_第20张图片](http://img.e-com-net.com/image/info8/0a9444b11a324d8997af580f0e10d865.jpg)
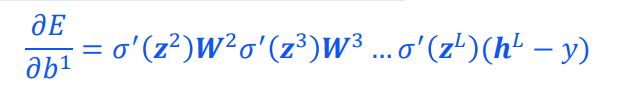
![[机器学习导论]——第三课——神经网络Ⅱ_第21张图片](http://img.e-com-net.com/image/info8/fb79e1d771d5417dadd65a0db894f1b0.jpg)