(2014)Generative Adversarial Nets 论文解读

Generative Adversarial Nets–生成对抗网络

作者：Ian J. Goodfellow, Jean Pouget-Abadie∗, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair†, Aaron Courville, Yoshua Bengio‡

---

论文阅读过程中也遇到了一些问题，穿插在文中提出了，希望有理解的人回答一下。

Abstract

1.本篇文章完成了什么？

• 提出建立一个类似对抗过程的模型来评估生成模型(generative models)生成数据的质量。

2.文章所提框架的特点：

• 同时训练数据生成模型G和评估G所生成数据的模型D。
• G的训练过程是为了增加D犯错误的概率(错把模拟数据认为是真实数据)。
• 在任意函数空间中，存在一个为一解，使得G能够很好的产生出模拟真实分布的数据，也使得D在任何位置值都为1/2。

3.文章所提模型优势：

• 在G和D由多层感知机构成的情况下，整个系统仍然可以适应反向传播进行训练。
• 不需要任何马尔科夫链或展开推理网络(unrolled approximate inference networks)。

1. Introduction

1.在Dropout算法以及反向传播算法的影响下，Discriminative模型进来取得了很大的成功。

2.Generative模型的难点：

• 由于极大似然估计和其他方法中出现很多的难以计算的概率问题。
• 难以在生成环境中利用分段线性单元的优点。

3.对抗网络模型的特点：

• 生成模型(Generator)与判别模型(Discriminator)一直是对抗关系。
• 判别模型一直在区分数据是由生成模型产生还是来自真实数据库(我们可以理解为为打假)。
• 生成模型一直在努力输出让判别模型难以分辨的数据(可以理解为造假)。

2. Related work

这一部分主要讲述前人的研究工作，不做叙述。

3. Adversarial nets

这一部分主要讲述算法，先解释一下计算公式中各个变量的含义。

• 数据:$x$
• 数据$x$的分布：$p_g$
• 输入噪声的先验分布:$f_z(z)$
• 数据空间映射：$G(z;{\theta }_g)$，其中G是由含有参数${\theta }_g$的多层感知机表示的可微函数，可以理解为产生的数据。
• 多层感知机函数：$D(x;{\theta }_d)$，输出一个单独的标量，标量用来评价数据的质量。
• 真实数据分布：$D(x)$表示$x$来自真实数据分布而不是$p_g$的概率。通过训练$D$来最大化分配正确标签给训练样本和$G$产生的样本的概率。同时训练$G$来最小化$log(1-D(G(z)))$，$D(G(z))$可以理解为数据$G(z)$打的分数。
• 实际上对$D$和$G$的训练是关于值函数$V(G,D)$的极小化极大化的博弈问题。
  其计算公式如下：
  
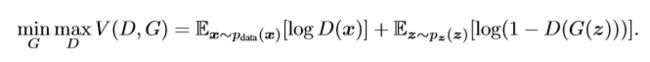
  分析上式，$x$是真实数据，$D(X)$表示给真实数据打的分数，$G(z)$表示生成器生成的数据，$D(G(z))$表示给生成数据打的分数。我们希望$D(x)$大的同时$D(G(z))$也很大。

疑问：论文中提到上式可能无法为$G$提供足够的梯度来学习，在刚开始学习时$G$的效果差，因此$D$很容易给生成的数据打低分。在这种情况下，$log(1-D(G(z)))$很容易饱和，因此遇去训练$G$去最小化$log(1-D(G(z)))$，不如训练$G$去最大化$logD(G(z))$。

不应该最大化$log(1-D(G(z)))$吗，$D(G(Z))$最好是值很小？

解答：突然想明白了，其实对抗网络的最终目标是生成高质量的图片，因此最后Generator生成的图片应该最大程度的能“欺骗”Disciminator，也就是$D(G(Z))$值很大，接近于1。

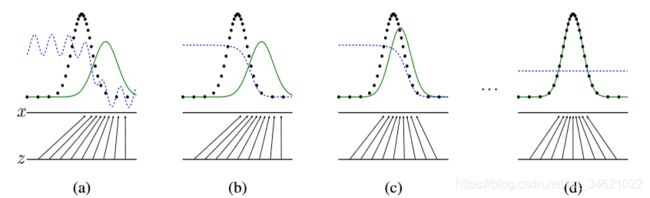
图1.训练对抗的生成网络时，同时更新判别分布（$D$，蓝色虚线）使$D$能区分数据生成分布$p_x$（黑色虚线）中的样本和生成分布$p_g$ ($G$，绿色实线) 中的样本。下面的水平线为均匀采样$z$的区域，上面的水平线为$x$的部分区域。朝上的箭头显示映射$x=G(z)$如何将非均匀分布$p_g$作用在转换后的样本上。$G$在$p_g$高密度区域收缩，且在$p_g$的低密度区域扩散。
($a$)考虑一个接近收敛的对抗的模型对：$p_g$与$p_{data}$相似，且$D$是个部分准确的分类器。
($b$)算法的内循环中，训练$D$来判别数据中的样本，收敛到：$D^{\ast }(X)=\frac{p_{data}(x)}{p_{data}(x)+p_g(x)}$。
($c$)在$G$的11次更新后，$D$的梯度引导$G(z)$流向更可能分类为数据的区域。
($d$)训练若干步后，如果$G$和$D$性能足够，它们接近某个稳定点并都无法继续提高性能，因为此时$p_g=p_{data}$。判别器将无法区分训练数据分布和生成数据分布，即$D(x)=\frac{1}{2}$。

Theoretical Results

算法：

在训练时我们通常选择先训练k次Discriminator，再训练一次Generator。算法的讲解过程在此博客中的第三页，不再赘述。截图放在下面，可能不太清晰。

4.1 Global Optimality of $p_g=p_{data}$

当$p_g=p_{data}$时，我们会得到最优的对抗模型。
为了取得这样的结果，我们最先想到的是对于任何给定的$G$我们训练出好的$D$。

5. Experiments

1.使用的数据集：Minist、TFD以及CIFAR-10。

2.Generator使用的激活函数有ReLU和sigmoid，Discirminator使用的激活函数是maxout。Dropout算法被用于判别器网络的训练。虽然理论框架可以在生成器的中间层使用Dropout和其他噪声，但是这里仅在生成网络的最底层使用噪声输入。

3.对G生成的样本拟合高斯Parzen窗口，并报告该分布下的对数似然，来估计$p_g$下测试集数据的概率。高斯分布中的参数$\sigma$通过验证集的交叉验证得到的。

4.Breuleux等人引入该过程用于不同的似然难解生成模型上，结果在下表中：
我们可以看到结果中方差很大，并且在高维模型中表现不好。

(原文翻译)表1.基于Parzen窗口的对数似然估计。MNIST上报告的数字是测试集上的平均对数似然以及在样本上平均计算的标准误差。在TFD上，我们计算数据集的不同折之间的标准误差，在每个折的验证集上选择不同的σ。在TFD上，在每一个折上对σ进行交叉验证并计算平均对数似然函数。对于MNIST，我们与真实值（而不是二进制）版本的数据集的其他模型进行比较

经过训练后GAN生成的样本：

(翻译)图2.来自模型的样本的可视化。最右边的列示出了相邻样本的最近训练示例，以便证明该模型没有记住训练集。样品是完全随机抽取，而不是精心挑选。与其他大多数深度生成模型的可视化不同，这些图像显示来自模型分布的实际样本。此外，这些样本是完全不相关的，因为，采样过程并不依赖马尔科夫链混合。a) MNIST；b) TFD；c) CIFAR-10（全连接模型）；d) CIFAR-10（卷积判别器和“解卷积”生成器）

图3.通过在完整模型的zz空间的坐标之间进行线性内插获得的数字。

6. Advantages and disadvantages

1.优点:无需马尔科夫链，仅用反向传播来获得梯度，学习间无需推理，且模型中可融入多种函数。
2.缺点：(论文中说主要为$p_g(x)$的隐式表示，不理解)。训练期间G和D要同步，这个意思就是不要光训练G不训练D，也不要光训练D不训练G。以图片生成为例，Generator是需要Discriminator的反馈一点一点调整输出的，不可能一步成功，如果Generator一直在自己训练自己的，不管Discriminator给的评价，那么最后输出的结果肯定很糟糕。

下图是GAN于其他生成模型方法的比较：

7. Conclusions and future work

个人理解：
1.在第一条中论文指出可以在模型训练时加一些条件来约束输入，比如你的对抗网络生成一棵树，你可以规定想要输出的树是什么颜色。
2.给定输入$x$，可以通过训练任意一个模型来学习近似推理，以预测$z$。论文原话中提到：这和wake-sleep算法训练出的推理网络类似，但是它具有一个优势，就是在生成器训练完成后，这个推理网络可以针对固定的生成器进行训练。
3.(不理解，放原话)能够用来近似模型所有的条件概率p(xS∣xS̸)，其中$S$通过训练共享参数的条件模型簇的关于$x$索引的一个子集。本质上，可以使用生成对抗网络来随机拓展MP-DBM。

4. 怎样在标签数据有限时，提高分类器效果。
5. 如何提高模型效率，为协调G和D设计更好的方法，或者说在训练期间使用更好的噪声分布$z$，加速训练。