Leetcode(5) - 最长回文子串 - java版 -全解
题目
难度: 中等
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例1:
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例2:
输入: "cbbd"
输出: "bb"
一.暴力方法
此方法超出时间限制无法通过,不做推荐
思路:
选出所有子字符串可能的开始和结束位置,并检验它是不是回文。
实现:
class Solution {
public String longestPalindrome(String s) {
if(s.equals("")) return s;
int n = s.length(),start = 0,maxlen = 1;
for(int i =0;i= temp2 && j-i+1 >maxlen){
maxlen = j-i+1;
start = i;
}
}
return s.substring(start,start+maxlen);
}
}
二.最长公共子串法
此方法虽简单,但依旧超时,故仍不做推荐
思路:
先给出一个有缺陷的方案,
反转
S,使之变成S′。找到S和S′之间最长的公共子串,这也必然是最长的回文子串。
该方案的缺陷在于: ,当 S 的其他部分中存在非回文子串的反向副本时,最长公共子串法就会失败
如: S = “abacdfgdcaba” , S′ = “abacdgfdcaba”
S以及 S' 之间的最长公共子串为 “abacd”。显然,这不是回文。
解决此缺陷的方法也很简单, 每当我们找到最长的公共子串的候选项时,都需要检查子串的索引是否与反向子串的原始索引相同。
实现:
class Solution {
public String longestPalindrome(String s) {
if(s.equals("")) return s;
int n = s.length();
String s2 = new StringBuilder(s).reverse().toString(),ans = s.substring(s.length()-1);
for(int i =0; i ans.length() && s2.contains(sub) && s.indexOf(sub) == s.indexOf(new StringBuilder(sub).reverse().toString()))
ans = sub;
}
return ans;
}
}
三.动态规划
具体思路:
利用回文串的特性:
如果一个字串是回文字串,那么去掉左右两边的字符之后依然是回文。也可以说是一个回文字串,左右两边加上相同的字符,也是回文字串。
所以我们可以使用索引 i 和 j 来表示一个字符串从索引 i 到 j 的子串,
首先建立一个数组boolean[][] db
dp[i][j]表示索引i到j的子串是否是回文
dp[i][j] = true表示是回文,反之则为false
db的取值为: s.charAt(i) == s.charAt(j)&&j-i<2 || db[i+1][j-1]
长的子串dp[i][j]依赖于短的子串dp[i + 1][j - 1],所以由短到长依次计算
1.先计算一个字符,全为true
2.再计算两个字符,如果两个字符一样则为true
3.然后计算大于三个字符,直到整个字符串
实现:
class Solution {
public String longestPalindrome(String s) {
if(s.equals("")) return s;
int len = s.length(),left = 0,right = 0;
// db[i][j] 表示字符串区间 [i, j] 是否为回文串
boolean[][] db = new boolean[len][len];
// 注意,这里的遍历与平常我们对字符串的遍历不一样
for(int j = 0;jright-left){
left = i;
right = j;
}
}
return s.substring(left,right+1);
}
}
四.中心扩展算法
具体思路:
因为回文中心的两侧互为镜像,所以,我们可以从回文的中心去展开,并且,一共有2n-1个这样的中心
所含字母数为奇数的回文的中心处在某一个字符上,而所含字母数为偶数的回文的中心处在两数中间,
故两种情况都要考虑.
实现:
class Solution {
public String longestPalindrome(String s) {
if(s.equals("")) return s;
int start = 0,end = 0;
for(int i =0;iend-start+1){ //如果大于保存的最大回文长度,则计算并更新最大回文的位置
start = i -(len-1)/2;
end = i+len/2;
}
}
return s.substring(start,end+1);
}
public int expandAroundCenter(String s,int i,int j){
while(i>=0 && j 注意:
这里的start和end的代数式需要易错,书写时应注意.
五.Manacher算法
具体思路:
由于回文分为偶回文(比如 bccb)和奇回文(比如 bcacb),而在处理奇偶问题上会比较繁琐,所以这里我们使用一个技巧,具体做法是:在字符串首尾,及各字符间各插入一个字符(前提这个字符未出现在串里)。
举个例子:s="abbahopxpo",转换为s_new="#a#b#b#a#h#o#p#x#p#o#",如此,s 里起初有一个偶回文abba和一个奇回文opxpo,被转换为#a#b#b#a#和#o#p#x#p#o#,长度都转换成了奇数。
定义一个辅助数组int p[],其中p[i]表示以 i 为中心的最长回文的半径,例如:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| s_new[i] | # | a | # | b | # | b | # | a | # | h | # | o | # | p | # | x | # | p | # |
| p[i] | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 4 | 1 | 2 | 1 |
p[i]数组有一个性质,p[i]-1就等于该回文串在原串s中的长度
证明:
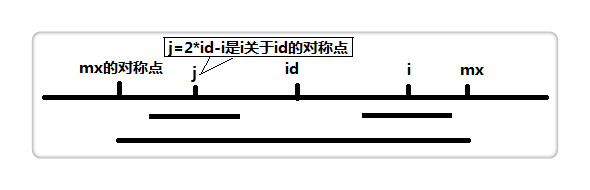
在转换后的字符串str_new中,所有的回文串的长度都是奇数,那么对于以i为中心的最长回文串的长度为2*p[i]-1,其中又有Len[i]个分隔符,所以在原字符串中的长度就是p[i]-1,那么剩下的工作就是求p数组, 如下图:
设置两个变量,mx 和 id 。mx 代表以 id 为中心的最长回文的右边界,也就是mx = id + p[id]。
假设我们现在求p[i],也就是以 i 为中心的最长回文半径,如果i < mx,如上图,那么:
if (i < mx)
p[i] = min(p[2 * id - i], mx - i);
2 * id - i为 i 关于 id 的对称点,即上图的 j 点,而p[j]表示以 j 为中心的最长回文半径,因此我们可以利用p[j]来加快查找。
集合实现:
class Solution {
public String longestPalindrome(String s) {
List s_new = new ArrayList<>();
for (int i = 0; i < s.length(); i++) {
s_new.add('#');
s_new.add(s.charAt(i));
}
s_new.add('#');
List Len = new ArrayList<>();
String sub = "";//最长回文子串
int sub_midd = 0;//表示在i之前所得到的Len数组中的最大值所在位置
int sub_side = 0;//表示以sub_midd为中心的最长回文子串的最右端在S_new中的位置
Len.add(1);
for (int i = 1; i < s_new.size(); i++) {
if (i < sub_side) {//i < sub_side时,在Len[j]和sub_side - i中取最小值,省去了j的判断
int j = 2 * sub_midd - i;
if (j >= 2 * sub_midd - sub_side && Len.get(j) <= sub_side - i) {
Len.add(Len.get(j));
} else Len.add(sub_side - i + 1);
} else //i >= sub_side时,从头开始匹配
Len.add(1);
while ((i - Len.get(i) >= 0 && i + Len.get(i) < s_new.size()) && (s_new.get(i - Len.get(i)) == s_new.get(i + Len.get(i))))
Len.set(i, Len.get(i) + 1);//s_new[i]两端开始扩展匹配,直到匹配失败时停止
if (Len.get(i) >= Len.get(sub_midd)) {//匹配的新回文子串长度大于原有的长度
sub_side = Len.get(i) + i - 1;
sub_midd = i;
}
}
sub = s.substring((2 * sub_midd - sub_side) / 2, sub_side / 2);//在s中找到最长回文子串的位置
return sub;
}
}
数组实现:
class Solution {
public String longestPalindrome(String s) {
// 拼接得到新串
String s_new = "*";
for(int j =0;j-1&& i+p[i] mx){
mx = i+p[i];
id = i;
}
// 更新最大回文长度的中心索引以及边界索引
if(p[i] >p[sub_mid]){
sub_mid =i;
sub_side = i+p[i]-1;
}
}
return s.substring((2 * sub_mid - sub_side) / 2, sub_side / 2);
}
}
注意: 上面分割字符串得到返回值的方式有很多种,应灵活处理.
参考文章
- 最长回文子串(Java 动态规划)Longest Palindromic Substring
- 四种方法求最长回文串
- [白乾涛的Blog]
- Manacher算法总结
- [Manacher算法]
- Leetcode(5)-最长回文子串(包含动态规划以及Manacher算法)