双连通域分解(强连通分量)

对于无向图G。若删除顶点v后G所包含的连通图增多，则称v为切割节点(cut vertex)或关节点(articulation point)。不含任何关节点的图被称为双连通图(强连通图)。任一无向图都都可以看做是若干个极大的双连通子图组合而成，这样的子图被称为双连通域(强联通分量)(bi-connected component)。

下图中c就为关节点

蛮力算法

先通过BFS或者DFS搜索出图G所含连通域的数目；然后逐一枚举每一个顶点v，暂时将它从图G中删除。在此搜索统计出此时的图G\{v}所含连通域的数目。如果顶点v是关节点，当且仅当图G\{v}包含的连通域多于图G。

但算法非常耗时，为

可行算法

在经过DFS搜索的搜索树中，DFS树中的叶节点，不可能成为原图中的关节点。如DFS树的根节点若至少有两个分支，则必是一个关节点。

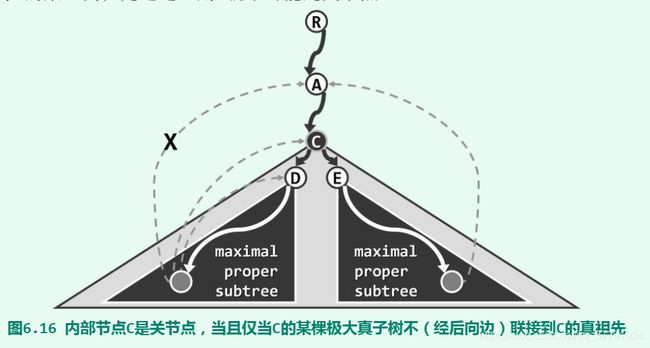
内部节点的判定铜过通过判断某节点的真子树和真祖先。如下图如节点c的移除导致其某一课(比如以D为根的)真子树与其真祖先(比如A)之间无法连通，则C必为关节点。反之，若C的所有真子树都能(如以E为根的子树那样)与C的某一真祖先连通，则C就不可能是关节点。

 

实现一 Kosaraju 算法

先理解下转置图的，如果与图G中的每条边都相反的图被称为转置图

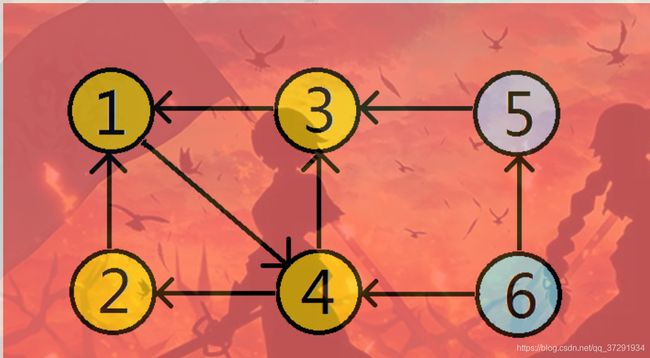
1> 任选一点进行DFS，标记其发现时间St和完成时间Et，将顶点按照完成时间从小到大依次放入栈中。

从1结点开始进行DFS，左边是发生时间St，右边是完成时间Et

 按照完成时间从小到大压如栈中

2> 将图G进行转置，得到转置图，从栈中依次弹出并进行DFS并且边进行分类标记，之后在从栈中找到新的起点(没有被分类标记的点)进行DFS并且在进行分类标记(这里的分类标记为上一次的加一)，直到栈的元素全部被弹出。

3> 上一步中分类标记值相同的结点所构成的一棵树，就为强联通分量。

时间复杂度 (领接表)，在实际操作中要比Tarjan算法要慢。

模板

#include "cstdio"
#include "iostream"
#include "algorithm"

using namespace std ;

const int maxN = 10010 , maxM = 50010;

struct Kosaraju { int to , next ; } ;

Kosaraju E[ 2 ][ maxM ] ;
bool vis[ maxN ];
int head[ 2 ][ maxN ] , cnt[ 2 ] , ord[maxN] , size[maxN] ,color[ maxN ];

int tot , dfs_num  , col_num , N , M  ;

void Add_Edge( int x , int y , int _ ){//建图 
         E[ _ ][ ++cnt[ _ ] ].to = y ;
         E[ _ ][ cnt[ _ ] ].next = head[ _ ][ x ] ;
         head[ _ ][ x ] = cnt[ _ ] ;
}

void DFS_1 ( int x , int _ ){
         dfs_num ++ ;//发现时间 
         vis[ x ] = true ;
         for ( int i = head[ _ ][ x ] ; i ; i = E[ _ ][ i ].next ) {
                 int temp = E[ _ ][ i ].to;
                 if(vis[ temp ] == false) DFS_1 ( temp , _ ) ;
         }
         ord[(N<<1) + 1 - (++dfs_num) ] = x ;//完成时间加入栈 
}

void DFS_2 ( int x , int _ ){
         size[ tot ]++ ;// 强连通分量的大小 
         vis[ x ] = false ;
         color[ x ] = col_num ;//分类
         for ( int i=head[ _ ][ x ] ; i ; i = E[ _ ][ i ].next ) {
                 int temp = E[ _ ][ i ].to;
                 if(vis[temp] == true) DFS_2(temp , _);
         } 
}

int main ( ){
         scanf("%d %d" , &N , &M );
         for ( int i=1 ; i<=M ; ++i ){
                 int _x , _y ;
                 scanf("%d %d" , &_x , &_y ) ;
                 Add_Edge( _x , _y , 0 ) ;//原图的邻接表 
                 Add_Edge( _y , _x , 1 ) ;//逆图的邻接表 
         }
         for ( int i=1 ; i<=N ; ++i ) 
                 if ( vis[ i ]==false ) 
                          DFS_1 ( i , 0 ) ;//原图的DFS 

         for ( int i = 1 ; i<=( N << 1) ; ++i ) {
                 if( ord[ i ]!=0 && vis[ ord[ i ] ] ){
                          tot ++ ; //强连通分量的个数 
                          col_num ++ ;//分类标记 
                          DFS_2 ( ord[ i ] , 1 ) ;
                 }
         }
         
         for ( int i=1 ; i<=tot ; ++i )
                 printf ("%d ",size[ i ]);
         putchar ('\n');
         for ( int i=1 ; i<=N ; ++i )
                 printf ("%d ",color[ i ]);
         return 0;
}