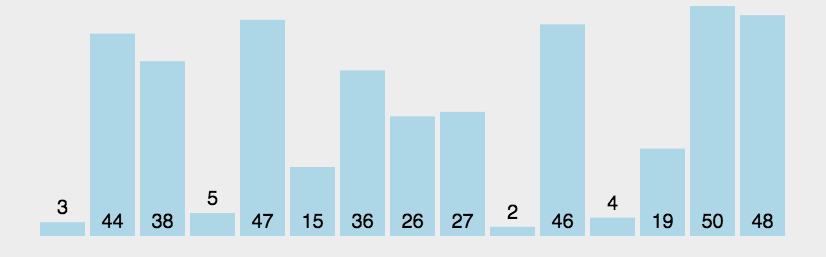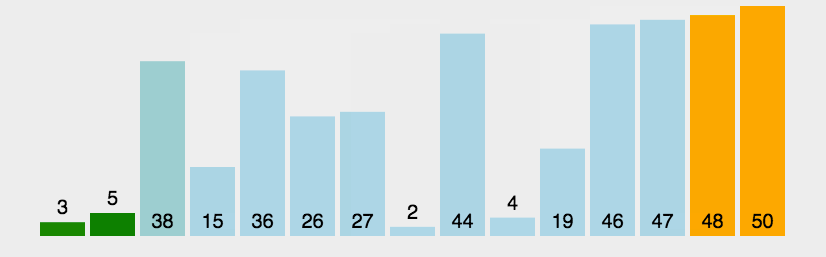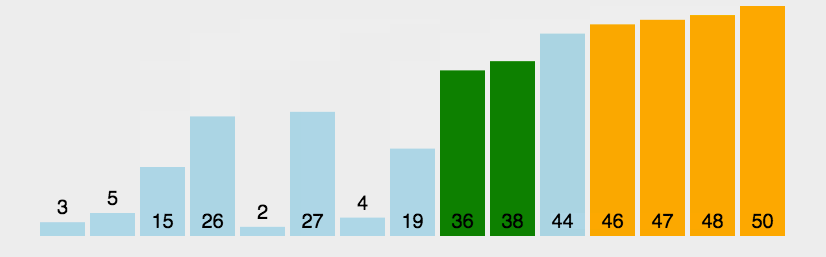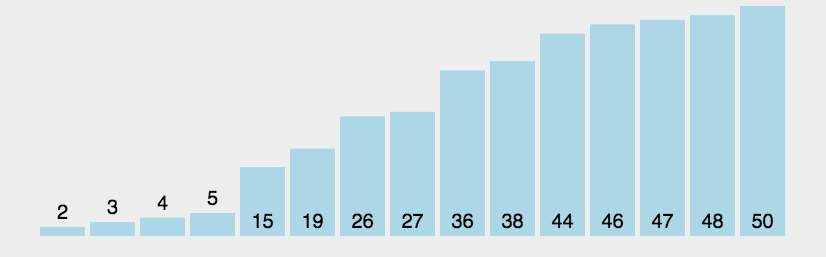面试准备：常用的基础排序算法

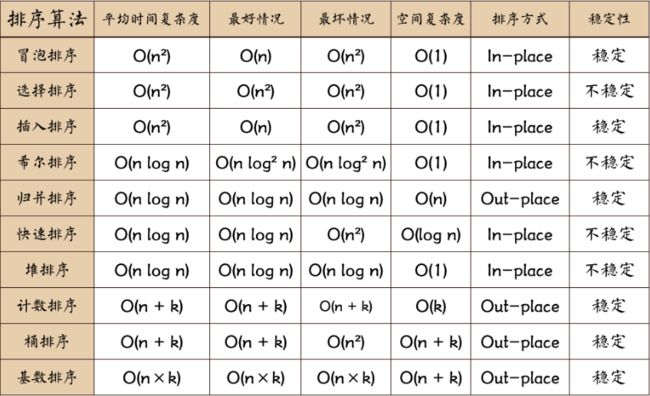
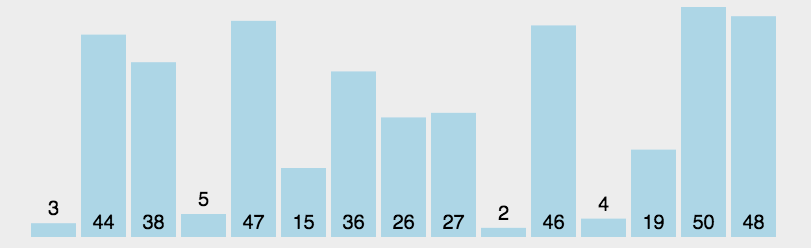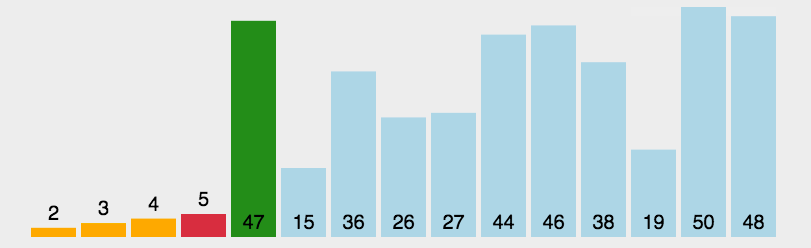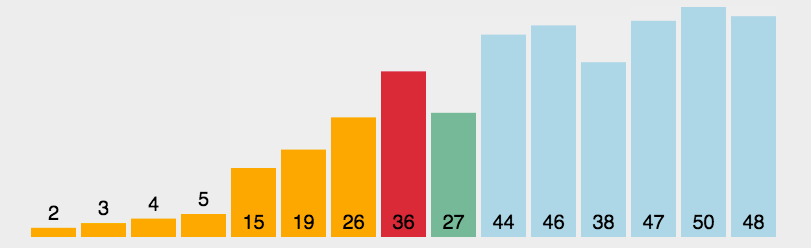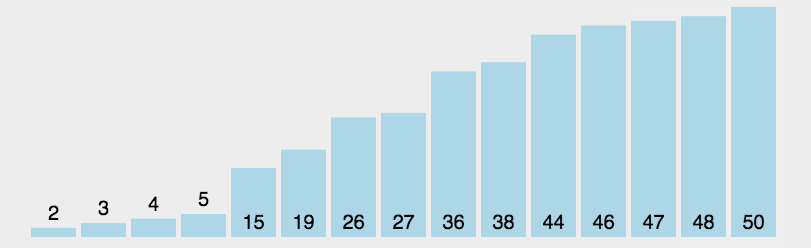
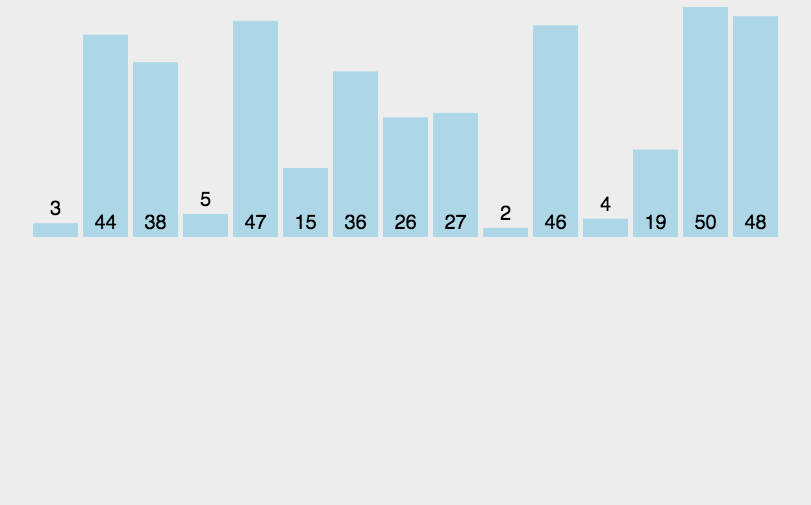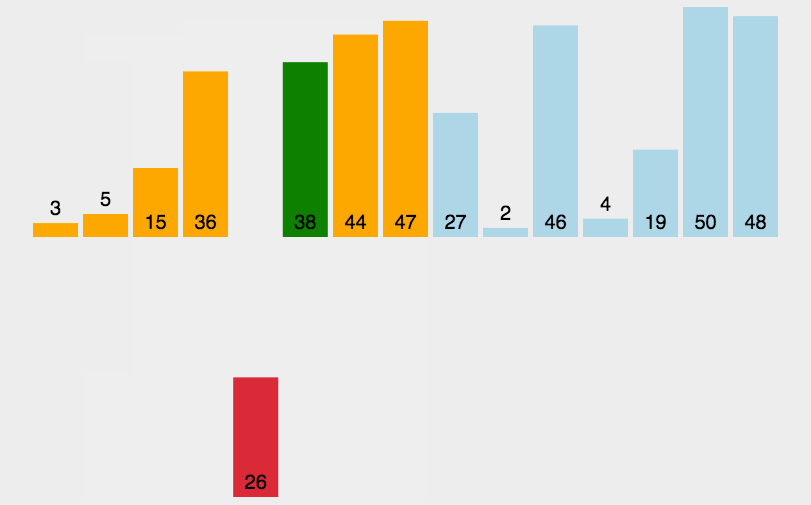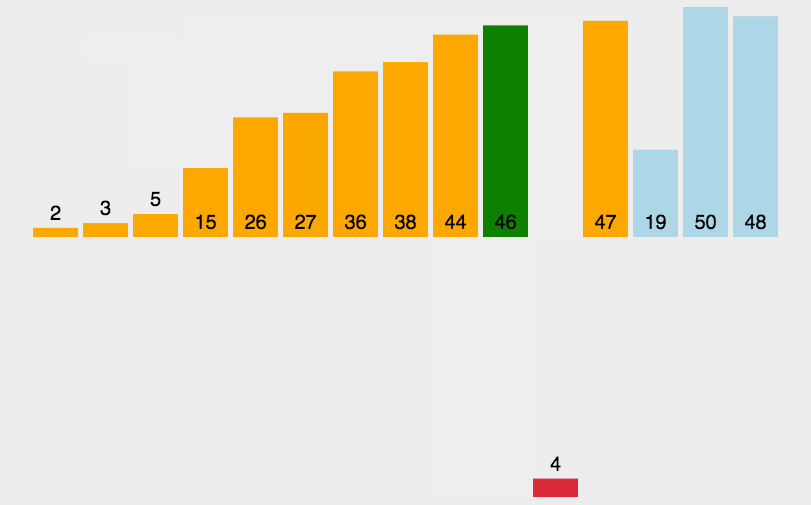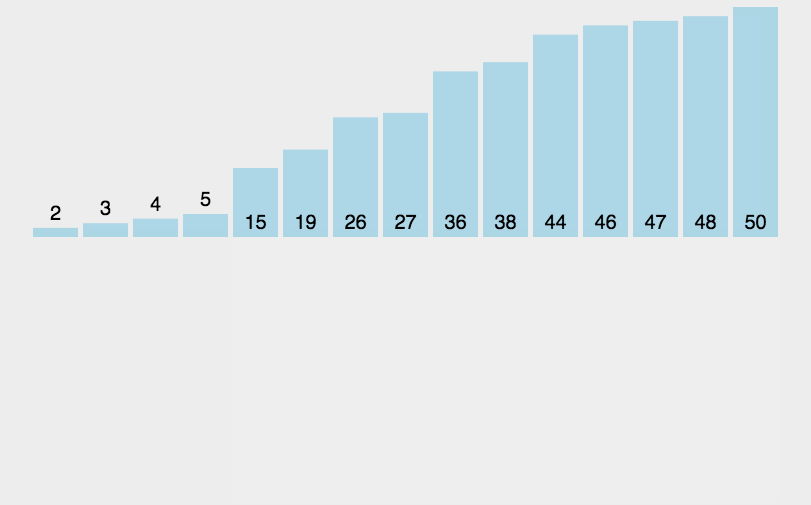
排序

冒泡排序

冒泡排序很简单，如果遇到前面的元素比后面的元素大，那么就交换他们的位置；每次遍历完成后，会确定最后k个元素一定是升序的，k是遍历的次数。

public class Solution {
    public void bubbleSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            for (int j = 0; j < arr.length - i - 1; j++) {
                if (arr[j] > arr[j + 1]) {
                    exchange(arr, j, j + 1);
                }
            }
        }
        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }

    public void exchange(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

冒泡排序为了节省一点时间，使用了一个标志位boolean来表示这一次遍历是否有交换过，如果一次都没有交换过，说明整个数组已经有序了。

平均时间复杂度: $O(N^2)$
最好情况：$O(N)$，即一次遍历发现没有可以交换的；最坏情况：$O(N^2)$，即数组是倒序排列的
空间复杂度: $O(1)$
稳定性：稳定

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

选择排序

选择排序是每次选择一个最大（最小）的数字放到数组的最后（最前）面，它和冒泡排序很像，也是一次遍历能够确定一个数字的位置。

public class Solution {
    public void selectionSort(int[] arr) {
        for (int i = 0; i < arr.length; i++) {
            int currBiggestPos = 0;
            for (int j = 1; j <= arr.length - i - 1; j++) {
                if (arr[j] > arr[currBiggestPos]) {
                    currBiggestPos = j;//找到最大的数所在下标
                }
            }
            //交换最大的数到后面去
            exchange(arr, arr.length - i - 1, currBiggestPos);
        }
        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }

    public void exchange(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

平均时间复杂度: $O(N^2)$
最好情况和最坏情况均为$O(N^2)$
空间复杂度:$ O(1)$
稳定性：不稳定

插入排序

插入排序是在要排序的一组数中，假定前n-1个数已经排好序，现在将第n个数插到前面的有序数列中，使得这n个数也是排好顺序的。
所以第k次遍历，就是将第k+1个数插入到前面k个数的特定位置上，使得这k+1个数是排好序的。插入方式是比较当前值和数组值的大小，如果比数组值大那么说明找到了插入位置，否则要继续向前找，并且将当前数组的值移到后面一位。

public class Solution {
    public void insertionSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int curr = arr[i + 1];
            int preIndex = i;
            while (preIndex >= 0 && arr[preIndex] > curr) {
                arr[preIndex + 1] = arr[preIndex];//后移一位
                preIndex--;
            }
            arr[preIndex + 1] = curr;
        }
        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }
}

平均时间复杂度: $O(N^2)$
最好情况和最坏情况均为$O(N^2)$
空间复杂度: $O(1)$
稳定性：稳定

希尔排序

希尔排序实际上就是插入排序，可以从下面的代码看出（注意对比插入和希尔的注释），希尔排序实际上使用gap来表示间隔的，当gap是1的时候实际上就是上面的插入排序。

public class Solution {
    public void insertionSort(int[] arr) {
        int gap = arr.length / 2;
        while (gap > 0) {
            for (int i = 0; i < arr.length - gap; i++) {
                int curr = arr[i + gap];
                int preIndex = i;
                while (preIndex >= 0 && arr[preIndex] > curr) {
                    arr[preIndex + gap] = arr[preIndex];//后移gap位
                    preIndex -= gap;
                }
                arr[preIndex + gap] = curr;
            }
            gap /= 2;
        }

        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }
}    

平均时间复杂度: $O(N\ast LogN)$
空间复杂度: $O(1)$
稳定性：不稳定

• 为什么同样是插入排序，希尔排序的复杂度却是$O(N\ast logN)$呢？即，为啥希尔能突破$O(N^2)$的界？
  可以用逆序数来理解，假设我们要从小到大排序，一个数组中取两个元素如果前面比后面大，则为一个逆序，容易看出 排序的本质就是消除逆序数 ，可以证明对于随机数组，逆序数是$O(N^2)$的，而如果采用“交换相邻元素”的办法来消除逆序，每次正好只消除一个，因此必须执行$O(N^2)$的交换次数，这就是为啥冒泡、插入等算法只能到平方级别的原因，反过来，基于交换元素的排序要想突破这个下界，必须执行一些比较， 交换相隔比较远的元素，使得一次交换能消除一个以上的逆序，希尔、快排、堆排等等算法都是交换比较远的元素，只不过规则各不同罢了

归并排序

归并排序是将两段排序好的数组合并成一个排序数组，merge方法就是简单的有序数组的合并，mergeSort方法就是典型的分而治之的思想。

public class Solution {
    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] arr = new int[]{2, 3, 1, 4, 5, 2, 1, 4, 7};
        solution.mergeSort(arr, 0, arr.length - 1);

        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }

    public void mergeSort(int[] arr, int start, int end) {
        if (start >= end) return;
        else {
            int mid = (end + start) >>> 1;
            mergeSort(arr, start, mid);
            mergeSort(arr, mid + 1, end);
            merge(arr, start, mid, end);//合并两个数组
        }
    }

    public void merge(int[] arr, int start, int mid, int end) {
        int[] tmp = new int[end - start + 1];
        //两个数组范围分别是 [start,mid]和[mid+1,end]
        int startLeft = start, startRight = mid + 1;
        int index = 0;
        while (startLeft <= mid && startRight <= end) {
            if (arr[startLeft] < arr[startRight]) {
                tmp[index++] = arr[startLeft++];
            } else {
                tmp[index++] = arr[startRight++];
            }
        }
        while (startLeft <= mid) {
            tmp[index++] = arr[startLeft++];
        }
        while (startRight <= end) {
            tmp[index++] = arr[startRight++];
        }
        index = 0;
        for (int i = start; i <= end; i++) {
            arr[i] = tmp[index++];
        }
    }
}

平均时间复杂度: $O(N\ast LogN)$
空间复杂度: $O(N)$
稳定性：稳定

快速排序

通过一趟排序将待排记录分隔成独立的两部分，其中分割partition的左边都是比partitiion小的，右边都是比partition大的。

public class Solution {
    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] arr = new int[]{2, 3, 1, 4, 5, 2, 1, 4, 7};
        solution.quickSort(arr, 0, arr.length - 1);

        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }

    public void quickSort(int[] arr, int start, int end) {
        if (start < end) {
            int partition = findPartition(arr, start, end);
            quickSort(arr, start, partition - 1);
            quickSort(arr, partition + 1, end);
        }
    }

    public int findPartition(int[] arr, int start, int end) {
        int curr = arr[start];
        while (start < end) {
            //从右向左找不符合基准的
            while (start < end && arr[end] >= curr) {
                end--;
            }
            arr[start] = arr[end];
            //从左向右找不符合基准的
            while (start < end && arr[start] <= curr) {
                start++;
            }
            arr[end] = arr[start];
        }
        arr[start] = curr;
        return start;
    }
}

平均时间复杂度: $O(N\ast LogN)$
空间复杂度: $O(LogN)$，递归的时候使用的栈空间
稳定性：不稳定

堆排序

堆排序首先会建立大顶堆，大顶堆一定能保障顶点是最大值，所以每次遍历交换最大元素到数组末尾表示确定即可。

public class Solution {
    public void heapSort(int[] arr) {
        int len = arr.length;
        //建立堆
        buildHeap(arr, len);

        while (len > 1) {
            exchange(arr, 0, len - 1);
            len--;
            heapify(arr, 0, len);
        }
        Arrays.stream(arr).forEach(o -> System.out.print(o + " "));
    }

    public void buildHeap(int[] arr, int len) {
        for (int i = len / 2; i >= 0; i--) {//从后往前建立大顶堆
            heapify(arr, i, len);
        }
    }

    public void heapify(int[] arr, int parent, int len) {
        int large = parent;
        int leftChild = parent * 2 + 1;
        int rightChild = parent * 2 + 2;
        //找到最大的子节点
        if (leftChild < len && arr[leftChild] > arr[large]) {
            large = leftChild;
        }
        if (rightChild < len && arr[rightChild] > arr[large]) {
            large = rightChild;
        }
        
        if (large != parent) {
            exchange(arr, large, parent);
            heapify(arr, large, len);
        }

    }

    public void exchange(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

平均时间复杂度: $O(N\ast LogN)$
空间复杂度: $O(1)$
稳定性：不稳定

计数排序

计数排序对数组元素有要求，在使用额外O(N)的数组的前提下，数组属于0-k的元素。当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 O(N + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

平均时间复杂度: $O(N+K)$
空间复杂度: $O(N)$
稳定性：稳定

桶排序

桶排序是计数排序的升级版，即将每个元素放到有范围的桶内，然后在桶内使用其他排序算法来做排序。
第一步放到桶内：

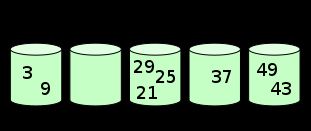
第二步，使用其他排序算法做排序（比如插入排序）：

为了使桶排序更加高效，我们需要做到这两点：

• 在额外空间充足的情况下，尽量增大桶的数量
• 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中

平均时间复杂度: $O(N+K)$
空间复杂度: $O(N)$
稳定性：稳定

基数排序

• 计数排序：每个桶只存储单一键值；
• 桶排序：每个桶存储一定范围的数值；
• 基数排序：根据键值的每位数字来分配桶；

基数排序最难想到的还是bucket的数据结构怎么表示，一般这样的bucket会用数组+链表的形式表示，但是这占用的空间会变大，下面的代码bucket表示方式是使用count的方式来做的，可以好好体会一下。

public class Solution {

    public void radixSort(int[] arr) {
        //待排序列最大值
        int max = arr[0];
        int exp;//指数

        //计算最大值，以确定exp最大应该是多少
        for (int anArr : arr) {
            if (anArr > max) {
                max = anArr;
            }
        }

        //从个位开始，对数组进行排序
        for (exp = 1; max / exp > 0; exp *= 10) {
            //存储待排元素的临时数组
            int[] temp = new int[arr.length];
            //分桶个数
            int[] buckets = new int[10];

            //将数据出现的次数存储在buckets中
            for (int value : arr) {
                //(value / exp) % 10 :value的最底位(个位)
                buckets[(value / exp) % 10]++;
            }

            //更改buckets[i]，为了找到每一个arr[i]的正确位置，所以需要加上前面的个数
            for (int i = 1; i < 10; i++) {
                buckets[i] += buckets[i - 1];
            }

            //将数据存储到临时数组temp中
            for (int i = arr.length - 1; i >= 0; i--) {
                temp[buckets[(arr[i] / exp) % 10] - 1] = arr[i];
                buckets[(arr[i] / exp) % 10]--;
            }

            //将有序元素temp赋给arr
            System.arraycopy(temp, 0, arr, 0, arr.length);
        }

    }
}

平均时间复杂度: $O(N\ast K)$，K表示最大数的长度
空间复杂度: $O(N)$
稳定性：稳定