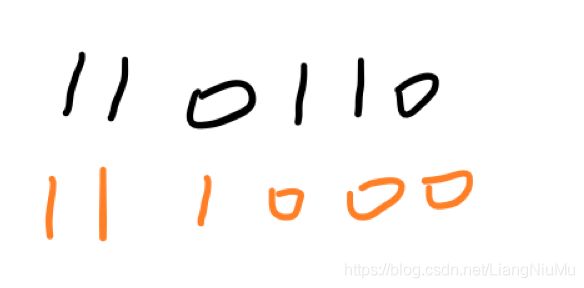Codeforces Round #648 (Div. 2)

这次状态不好，总是wa题，心态都有点炸了，这里写下CDEF

传送门

C. Rotation Matching

主要思路： 主要是看两个相同的值的差距距离，然后计算差距距离最多的数值是多少即可

解题思路：

• 这题还是比较简单的思维题
• 首先我们可以想到我们计算两个数组相同值差的距离，这里我们用： 第一个数组的值的位置 - 第二个数组值的位置 + n % n 即可，表达式：（res是记录的差值为x时的个数）

scanf("%d",&b[i]);
int x = (aa[b[i]]+(n-i)) % n;
 res[x] ++;

• 最后我们 0 — n 找出这个最大值即可，注意一下这里从0开始（wa了2发，哭死）

代码：

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 200010;

int a[N], b[N];
int aa[N], bb[N];
int res[N * 2];

int main(){
    int n;
    scanf("%d",&n);
    for (int i = 1; i <= n; i++){
        scanf("%d",&a[i]);
        aa[a[i]] = i;
    }
    for (int i = 1; i <= n ; i++){
        scanf("%d",&b[i]);
        int x = (aa[b[i]]+(n-i)) % n;
        res[x] ++;
    }

    int mx = 0;
    for (int i = 0 ;  i < n * 2; i++){
        mx = max(mx,res[i]);
    }
    printf("%d\n",mx);
    return 0;
}

D. Solve The Maze

主要思路： 将’B’周围都换成墙（如果旁边接‘G’，那么肯定 no，记得标记一下），然后从右下角的点dfs搜索，最终判断G的个数与原图的是否相同即可。

解题思路：

• 首先我们的’B’ 是不能逃出的，也就是说 ‘B’ 的周围设置成墙即可了，如果是G，那么直接为NO
• 设置成墙后，如果有G 与 B 相邻，那么肯定是不行的，因为如果G可以逃，那么B肯定也是可以的
• 然后我们从右下角的位置开始dfs找G的位置，找到后设置该位置为墙，因为不能来回找。
• 然后我们判断，如果右下角的位置是# ，那么肯定输出NO
• 如果原图G 的个数为0，那么肯定是YES
• 如果dfs找的G的个数与原图G的个数不同，那么肯定是NO
• 最后注意细节判断即可，代码还可以简化

代码：

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 200010;

string ans[55];

int idx[4] = {0,0,1,-1};
int idy[4] = {1,-1,0,0};

int k = 0;
int n,m;
int cnt = 0;

void bfs1(int x, int y){
    for (int i = 0; i < 4; i ++){
        int xx = x + idx[i];
        int yy = y + idy[i];
        if (xx >= 0 && xx < n && yy >= 0 && yy < m ){
            if (ans[xx][yy] == 'G'){
                k = 1;
                return ;
            }
            else if (ans[xx][yy] == '.'){
                ans[xx][yy] = '#';
            }
        }
    }
}


void dfs(int x, int y){
	for (int i = 0; i < 4; i ++){
		int xx = x + idx[i];
        int yy = y + idy[i];
        if (xx >= 0 && xx < n && yy >= 0 && yy < m ){
            if (ans[xx][yy] == 'G'){
            	cnt ++;
            	ans[xx][yy] = '#';
            	dfs(xx,yy);
            }
            else if (ans[xx][yy] == '.'){
            	ans[xx][yy] ='#';
            	dfs(xx,yy);
            }
        }
	}
}

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        k = 0;
        cnt = 0;
        scanf("%d%d",&n,&m);
        for (int i = 0; i < n; i++){
            cin>>ans[i];
        }
        int num = 0;
        for (int i = 0; i < n; i ++){
            for (int j = 0; j < m; j++){
                if (ans[i][j] == 'B'){
                    bfs1(i,j); 
                }
                if (ans[i][j] == 'G'){
                	num ++;
                }
            }
        }
        if (ans[n-1][m-1] == '#') k =1;
        
        dfs(n-1,m-1);

        if (cnt != num){
        	k = 1;
        }

        if (num == 0) k = 0;

        if (k){
            puts("NO");
        }
        else{
            puts("YES");
        }
    }
    
    return 0;
}

E. Maximum Subsequence Value

主要思路： 可以推出一个结论，k > 3 时一定没k == 3时更优，所以我们暴力枚举，三重for循环找出最大值即可。

解题思路：

• 首先我们可以求出k == 1, k == 2时的最大值，这个很好理解，也就是自身组合，两个互相组合
• 这里说明一下为什么 k > 3时候没有 k == 3时候优，因为条件是max(1,k - 2)， 当k == 4时候，画下图吧：

• 这里 上面的代表 k== 3时候选的数字，下面是k == 2时选的，然后很显然，我们最终只能是110000，因为后面的2个1无法达到2位，然后我们肯定能从k == 3时候构造出前三位是1的或者更大的，因为条件限制了max(k-2,1)，在k为3的时候，我们只要出现一次就符合，k == 4我们要出现2个，那么就代表我们出现的位置必须是相同的，毫无意义，因此k > 3时，都没有k == 3时候更优。

代码：

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;

const int N = 510;

ll a[N];

int main(){
    int n;
    scanf("%d",&n);
    for (int i = 1; i <= n; i++){
        scanf("%lld",&a[i]);
    }
    ll ans = 0;
    for (int i = 1; i <= n; i++){
        for (int j = i; j <= n; j ++){
            for (int k = j; k <= n; k ++){
                ans = max(ans,a[i] | a[j] | a[k]);
            }
        }
    }
    printf("%lld\n",ans);
    return 0;
}

F. Swaps Again

主要思路：这里我们主要是找是否能改为相对应的，这里我们发现，我们的前后的对应位置是不会改变的，但是能改变他们的位置，所以我们让他们按照pair从小到大排序就OK，然后看是否相同

解题思路：

• 首先我们输入两个数组，然后我们用pair存储他们的相对位置，这里我们让小的在前，大的在后
• 然后我们对他们进行排序，这里我们排1 - n/2 即可，因为都是相对应的（后面都是前面位置对应过来的）
• 如果 n 是奇数，那么中间的位置肯定是不会变的，所以我们要判断中间位置是否相同
• 然后我们遍历看 1- n/2 的位置的前后是否对应即可

代码：

#include 
#include 
#include 
#include 

using namespace std;

typedef long long ll;
typedef pair <ll,ll> PII;

const int N = 550;

PII p[N],q[N];
ll a[N], b[N];

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        int n;
        scanf("%d",&n);
        for (int i = 1; i <= n; i++){
            scanf("%lld",&a[i]);
        }
        for (int i = 1 ; i <= n; i ++){
            scanf("%lld",&b[i]);
        }
        for (int i = 1; i <= n / 2;i ++){
            p[i] = {min(a[i],a[n - i + 1]),max(a[i],a[n - i + 1])};
            q[i] = {min(b[i],b[n - i + 1]),max(b[i],b[n - i + 1])};
        }
        sort(p + 1, p + n / 2 + 1);
        sort(q + 1, q + n / 2 + 1);
        int f = 1;
        if (n % 2 == 1 && a[n/2 + 1] != b[n/2 + 1]) f = 0;
        for (int i = 1; i <= n / 2; i ++){
            if (p[i].first != q[i].first || p[i].second != q[i].second){
                f = 0;
                break;
            }
        }
        if (f) puts("YES");
        else puts("NO");
    }
    return 0;
}