Google OR-Tools(一) Get Start

1 最优问题

我们先回顾下最优问题的概念。所谓最优化，就是指在满足某些约束条件的前提下，使得指定的目标函数极大化或极小化的过程。在工业界很多场景都可以归结为一个最优问题，利用合适的最优算法可以极大地提升效率和减小人工成本。通常情况下，现实的优化问题可以抽象为一个非线性规划，即：
$$\begin{array}{rl}minimize& f(\mathsf{x})\\ subjectto& g_i(\mathsf{x})\le 0i=1,...,m\\ & h_j(\mathsf{x})=0j=1,...,l\\ & {\mathsf{x}}^L\le \mathsf{x}\le {\mathsf{x}}^U\end{array}$$
其中，$\mathsf{x}=[x_1,x_2,...,x_n{]}^T$为$n$维列向量，各元素称为决策变量，而${\mathsf{x}}^L$，${\mathsf{x}}^U$表示决策变量的上界和下界；$f$称为目标函数或成本函数，$g$为不等式约束，$h$为等式约束。不同的优化问题通过适当的调整，总可以写成上面的形式。其实优化问题是个非常宽泛的概念，现在很火热的机器学习，其各种核心算法大多数也是在构建一个优化模型，例如神经网络经典的BP算法就属于一个无约束最优算法。
根据决策变量和目标函数的不同，一个非线性规划可以细分成下面这些特殊规划问题，通常我们对于特定的规划问题会有一些专门的算法来解算：

• 线性规划：所有的函数(包括目标函数和约束条件)都是线性的(在可行域内)，如果一个问题可以转化成线性规划，其求解起来是最简单的；
• 整数规划： 所有的决策变量必须是整数；
• 0-1规划：整数规划的进一步特殊化，决策变量只能在0和1中取值；
• 混合整数规划：某些决策变量要求是整数，另一些则是连续变量的线性规划；
• 混合非线性规划：某些决策变量要求是整数，另一些则是连续变量，约束条件和目标函数可以是非线性函数；
• 二次规划：在可行域中，目标函数是二次函数，所有约束条件都是线性函数；
• 凸规划：目标函数是凸函数或凹函数，可行域是凸集的规划；
• 组合优化问题：这类问题通常需要确定一个整数组合，或者在一些离散变量组合中选择一个最优的组合。某些组合优化问题可以作为线性规划问题进行求解，这样比较简单；但更多的组合优化问题是规模很大并且无法转变为线性规划的，我们通常只需要获得接近最优解的结果而不是绝对最优，这种情况下启发式算法用的比较多。

对各种优化问题，现在已经有很多特定的或一般性的算法，一些第三方公司会以这些算法为核心推出自己的优化软件工具，方便研究者和工程师的应用。那么对于优化工具的使用者来说，他们要做的最核心的工作将是优化问题建模。建模就是采用数学模型来描述物理问题，要根据实际情况抽象出决策变量、目标函数以及约束条件，表述成上述的非线性规划形式。通过建模，我们可以了解问题属于哪一类优化问题，从而采用合适的优化工具来处理。

2 Google OR-Tools的特点

Google OR-Tools是谷歌前才几年推出的优化套件，是一个相当新的优化库，其社区也是相当活跃，毕竟谷歌的影响力摆在那呢，可是也因为是谷歌的产品，其官网地址国内得才能访问。我个人在最近的一个项目里使用的就是Google OR-Tools，根据官方的资料和我自己的使用体验，总结下来有下面这些特点：

• 跨平台性：我认为这是它最吸引人的一点了，首先它的核心算法是基于C++写的，因此它天然地具有跨平台性，其次呢支持团队还分别针对C#、Java和python对核心算法库进行了封装，因此无论你是哪种技术栈都可以直接调用。
• 面向具体问题的套件组成：之所以叫它优化工具套件，是因为OR-Tools集合了各种优化算法，在软件层面，按照不同的优化问题类型，提供了不同的类库和接口。比如对最简单的线性规划问题，可以使用Linear Solver来解决；对于路径最优这个特定的问题，可以实例化一个RoutingModel对象来解算。
• 开源和开放：遵循Apache License 2.0，完全不用担心费用问题。另一方面，OR-Tools还支持第三方的求解器，你可以接入Gurobi, CPLEX这类商用求解器，或者SCIP, GLPK, GLOP等开源求解器来解算用OR-Tools建好的模型。
• 偏底层：OR-Tools更倾向于求解器系统，我们需要用它提供的接口构造好问题模型才能计算，因此对应用者的要求偏高，你需要有足够的数学抽象能力才能用好它。与之对应的也有更加一些面向对象的优化工具，比如Optaplanner，工作的重心是放在软件系统的领域建模上。

3 一个Demo

我们来基于OR-Tools写个小的Demo来体验一下。官网的教程是以Python为主的，只在前几章提供了其他语言的源码，我因为C#用的比较多，下面的Demo及后续文章的代码都在.net core平台实现。

我们来求解一个最简单的线性规划问题：
$$\begin{array}{rl}maximize& 3x+y\\ & 0\le x\le 1\\ & 0\le y\le 2\\ & x+y\le 2\end{array}$$
用OR-Tools解决优化问题，一般我们都会进行以下的步骤：

• 定义决策变量
• 定义约束
• 定义目标
• 声明实现了算法的solver对象
• 调用solver的方法进行计算得到结果

打开VS(最新的OR-Tools需要VS 2019的支持，低于2019的VS可能会报运行时异常)，新建一个.Net Core的控制台项目

在Nuget包管理页面中搜索并下载OR-Tools依赖

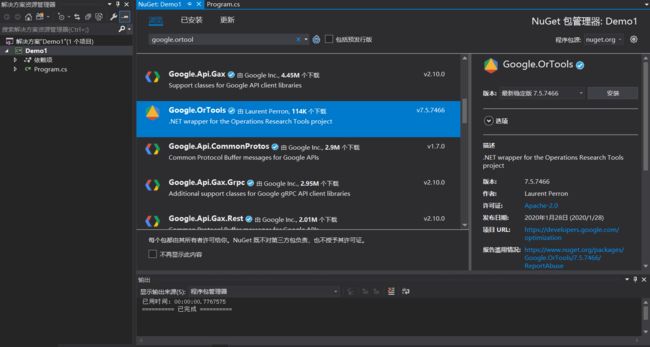
因为这是个标准的线性规划，我们只需要调用线性优化库来计算。在主程序中添加LinearSolver空间的引用

using Google.OrTools.LinearSolver;

首先我们定义solver对象，线性优化库的程序中是需要依靠solver对象来创建变、约束和目标的，因此这里没有完全依照上面描述的步骤：

//Create the linear solver with the GLOP backend
Solver solver = Solver.CreateSolver("SimpleLpProgram", "GLOP_LINEAR_PROGRAMMING");

接着定义变量，即$x$和$y$。MakeNumVar方法的三个参数分别表示变量的下限、上限和名字，这里通过变量定义，就已经加上了原问题的前两个约束。

 //Create variables
Variable x = solver.MakeNumVar(0.0, 1.0, "x");
Variable y = solver.MakeNumVar(0.0, 2.0, "y");
Console.WriteLine("Number of variables = " + solver.NumVariables());

我们需要定义第三个约束。一个Constraint对象就代表一个线性约束，我们通过SetCoefficient方法设置这两个变量的权值都是1，也就表示$0\le x+y\le 2$

//Create a Linear constraint
Constraint ct = solver.MakeConstraint(0.0, 2.0, "ct");
ct.SetCoefficient(x, 1);
ct.SetCoefficient(y, 1);
Console.WriteLine("Number of constraints = " + solver.NumConstraints());

现在就剩目标还没有定义了，通过solver对象创建Objective对象，并设定一个最大化的目标

//Create the objective function 
Objective objective = solver.Objective();
objective.SetCoefficient(x, 3);
objective.SetCoefficient(y, 1);
objective.SetMaximization();

最后我们就可以调用solver的Solve方法计算得到结果了

//Get the result
solver.Solve();
Console.WriteLine("Solution:");
Console.WriteLine("Objective value = " + solver.Objective().Value());
Console.WriteLine("x = " + x.SolutionValue());
Console.WriteLine("y = " + y.SolutionValue());

完整的程序：

using System;
using Google.OrTools.LinearSolver;

namespace Demo1
{
    class Program
    {
        static void Main(string[] args)
        {
            //Create the linear solver with the GLOP backend
            Solver solver = Solver.CreateSolver("SimpleLpProgram", "GLOP_LINEAR_PROGRAMMING");
            //Create variables
            Variable x = solver.MakeNumVar(0.0, 1.0, "x");
            Variable y = solver.MakeNumVar(0.0, 2.0, "y");
            Console.WriteLine("Number of variables = " + solver.NumVariables());
            //Create a Linear constraint
            Constraint ct = solver.MakeConstraint(0.0, 2.0, "ct");
            ct.SetCoefficient(x, 1);
            ct.SetCoefficient(y, 1);
            Console.WriteLine("Number of constraints = " + solver.NumConstraints());
            //Create the objective function 
            Objective objective = solver.Objective();
            objective.SetCoefficient(x, 3);
            objective.SetCoefficient(y, 1);
            objective.SetMaximization();
            //Get the result
            solver.Solve();
            Console.WriteLine("Solution:");
            Console.WriteLine("Objective value = " + solver.Objective().Value());
            Console.WriteLine("x = " + x.SolutionValue());
            Console.WriteLine("y = " + y.SolutionValue());
        }
    }
}