图论算法(一)深度优先搜索与广度优先搜索

深度优先搜索与广度优先搜索

图论基础知识

---

图是由一组顶点和一组能够将两个顶点相连的边组成的(可以无边,但是至少包含一个顶点):

• 一组顶点: 通常用V(vertex)表示顶点集合
• 一组边: 通常用E(edge)表示边集合

图的基本术语解释

[外链图片转存失败(img-SuflOrhS-1566875437171)(https://github.com/PandaHigh/image/blob/master/baseMean.png?raw=true)]

• 度 : 某个顶点的度数即为与其相连的边的总数
• 入度 : 存在有向图中, 所有的指向某个顶点的边的总数
• 出度 : 存在有向图中, 某个顶点指向其他顶点的边的总数
• 连通图 : 从任意一个顶点都存在一条路径到达另一个任意顶点,称这幅图是连通图.
• 连通分量 : 图中的连通图数量(连通图之间互无关联)
• 二分图 : 二分图是一种能够将所有顶点分为两部分的图,

图的分类

---

[外链图片转存失败(img-D96KImJe-1566875437172)(https://github.com/PandaHigh/image/blob/master/DirectedGraphAndUndirectedGgraph.png?raw=true)]
图可以分为无向图和有向图:

• 无向图: 在无向图中的边仅仅是两个顶点之间的连接
• 有向图: 在有向图中的边是有方向的,指的是箭头尾端的顶点指向箭头顶端的顶点, 无向图是特殊的有向图
  [外链图片转存失败(img-Vka0oFVs-1566875437173)(https://github.com/PandaHigh/image/blob/master/weightGraph.png?raw=true)]
  图可以分为有权图和无权图:
• 无权图: 每条边均没有权重,也可以理解为每条边的权重为1.
• 有权图: 每条边都有相应的权重(weight), 无权图是特殊的有权图.

[外链图片转存失败(img-r8s4gSHR-1566875437173)(https://github.com/PandaHigh/image/blob/master/connectedGraph.png?raw=true)]
图还可以分为连通图和非连通图:

• 连通图: 所有的顶点都有路径相连 (一个拥有v个顶点的连通图(即每个顶点都有联系)中,至少拥有v-1条边)
• 非连通图: 至少存在某两个顶点没有路径相连

图的表示方法

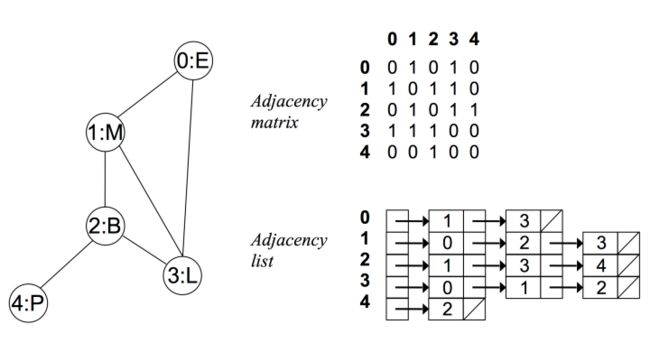
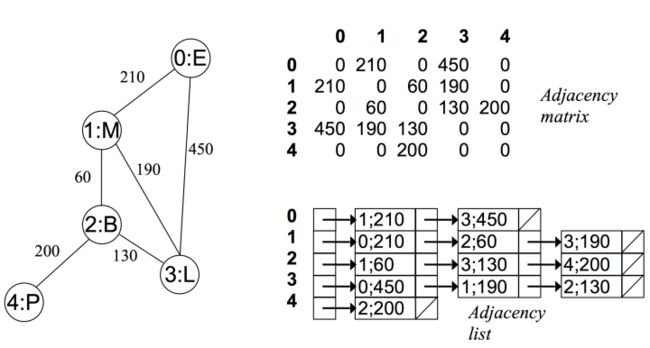
邻接矩阵

使用一个V乘以V的布尔矩阵, 当顶点v和顶点w之间有相连接的边时,定义布尔矩阵的第v行第w列的元素值为true,顶点与顶点之间没有相连接则定义为false.

邻接链表

使用一个以顶点为索引的列表数组,对于数组的每个位置都存储着一条与该顶点相连接的顶点构成的链表

例如在无向无权图中的:

在无向有权图中 :

在有向无权图中：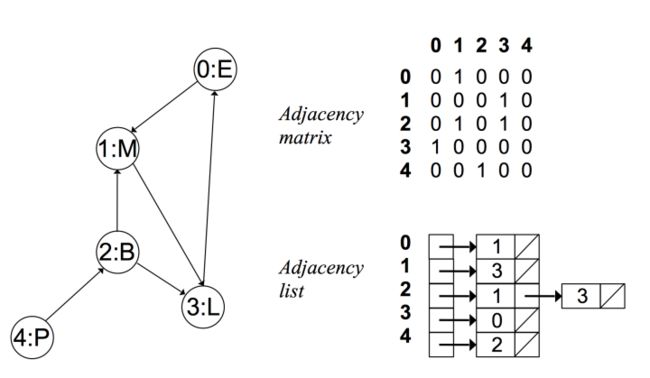
邻接矩阵与邻接矩阵对比:

• 邻接矩阵由于没有相连的边也占有空间，因此存在浪费空间的问题，而邻接链表则比较合理地利用空间
• 邻接链表比较耗时，牺牲很大的时间来查找，因此比较耗时，而邻接矩阵法相比邻接链表法来说，时间复杂度低,空间复杂度高。

图的遍历

---

深度优先搜索 (Depth First Search, DFS)

基本思路 : 深度优先搜索遍历图的方法是,从图中某个顶点出发

1. 访问指定的起始顶点
2. 若当前访问的顶点的邻接顶点有未被访问的,则任选一个顶点访问之; 反之, 退回到发现当前访问节点的那条边的起始节点; 直到与起始顶点相通的全部顶点都访问完毕.

[外链图片转存失败(img-XdljOIIF-1566875437176)(https://github.com/PandaHigh/image/blob/master/depthFirstSearch.png?raw=true)]

使用深度优先搜索查找图中的路径:

/** 深度优先搜索查找图中的路径 */
public class DepthFirstPaths {
    private boolean[] marked;//这个顶点是否已被访问
    private int[] edgeTo;//从起点到一个顶点的已知路径上的最后一个顶点
    private int s;//搜索起点

    public DepthFirstPaths(Graph G, int s){
        marked=new boolean[G.V()];
        edgeTo=new int[G.V()];
        this.s=s;
        dfs(G,s);
    }

    /**
     * 深度优先搜索
     * @param G 要搜索的图
     * @param v 搜索顶点
     */
    private void dfs(Graph G,int v){
        marked[v]=true;
        for (int w : G.adj(v)) {
            if(!marked[w]){
                edgeTo[w]=v;
                dfs(G,w);
            }
        }
    }

    /**
     * 是否有路径可以到达v
     * @param v 要到达的顶点
     * @return 有路径可以到达v为true,反之为false
     */
    public boolean hasPathTo(int v){
        return marked[v];
    }

    /**
     * 从起点s到达v顶点的路径
     * @param v 要到达的顶点
     * @return 路径
     */
    public Iterable pathTo(int v){
        if(!hasPathTo(v)){
            return null;//没有找到顶点v
        }
        Stack path = new Stack<>();//从终点v到起点s挨个压入栈中
        for(int x=v;x!=s;x=edgeTo[x]){
            path.push(x);
        }
        path.push(s);
        return path;
    }
}

广度优先搜索 (Breadth First Search, BFS)

基本思路 : 广度优先搜索,维护了一条队列

1. 先将指定的搜索顶点加入到队列中
2. 然后从队列中取出一个顶点,将其标记为已被访问
3. 得到该顶点的所有邻接顶点并将其中没有被访问过的顶点加入到队列中去
4. 转入步骤2继续从队列取出顶点,直到队列中不存在任何顶点.
   [外链图片转存失败(img-IiMeoKDz-1566875437177)(https://github.com/PandaHigh/image/blob/master/breadthFirstSearch.png?raw=true)]

使用广度优先搜索查找图中顶点路径 :

/** 广度优先搜索查找图中的路径 */
public class BreadthFirstPaths {
    private boolean [] marked;//这个顶点是否已被访问
    private int[] edgeTo;//从起点到一个顶点的已知路径上的最后一个顶点
    private int s;//搜索起点

    public BreadthFirstPaths(Graph G,int s){
        marked=new boolean[G.V()];
        edgeTo=new int[G.V()];
        this.s=s;
        bfs(G,s);
    }

    /**
     * 广度优先搜索
     * @param G 要搜索的图
     * @param s 搜索起点
     */
    private void bfs(Graph G,int s){
        Queue queue = new Queue<>();
        marked[s]=true;
        queue.enqueue(s);
        while(!queue.isEmpty()){
            int v=queue.dequeue();
            for (Integer w : G.adj(v)) {
                if(!marked[w]) {
                    marked[w] = true;
                    edgeTo[w] = v;
                    queue.enqueue(w);
                }
            }
        }
    }
   
    /**
     * 从起点s到达v顶点的路径
     * @param v 要到达的顶点
     * @return 路径
     */
    public Iterable pathTo(int v){
        if(!hasPathTo(v)){
            return null;
        }
        Stack path = new Stack();
        for(int x=v;x!=s;x=edgeTo[x]){
            path.push(x);
        }
        path.push(s);
        return path;
    }
}

深度优先搜索就像是一个人在走迷宫,不撞南墙不回头
而广度优先搜索就像是一组警察在搜查犯人,同时往不同的方向搜寻.

图论算法(一)深度优先搜索与广度优先搜索
图论算法(二)最小生成树
图论算法（三）最短路径