Python3——sklearn中回归模型的六种评估规则

评价回归模型的好坏需要计算真实值与预测值之间的误差关系，sklearn为我们提供了6种回归模型的评估规则，分别是

1.可释方差分数（explain variance score）

2.平均绝对误差（mean absolute error）

3.均方误差（mean squared error）

4.均方对数误差（mean squared logarithmic error），适用于具有指数增长的趋势的目标。

5.中值绝对误差（median absolute error），该函数不支持多输出。

6.决定系数分数（ score）

通常，函数以 _score 结尾返回一个值来最大化，越高越好。

            函数 _error 或 _loss 结尾返回一个值来 minimize （最小化），越低越好。

假设共有n个样本,真实值是,预测值是

1.可释方差分数（explain variance score）

explained_variance_score(y_true, y_pred, sample_weight=None, multioutput='uniform_average')

                              其中 multioutput : 有两个取值，分别是 ['raw_values', 'uniform_average']

                              “raw_values”:在多输出的情况下返回每个输出的误差集合。

                              “uniform_average”:在多输出的情况下返回所有输出的误差均值。

                                                                     

最佳模型的可释方差分数值为1，模型越差值越小。

 

2.平均绝对误差（mean absolute error）

mean_absolute_error(y_true, y_pred, sample_weight=None, multioutput='uniform_average')

                                                                       

平均绝对误差是非负值，模型越好MAE越接近零。

3.均方误差（mean squared error）

mean_squared_error(y_true, y_pred, sample_weight=None, multioutput='uniform_average')

注意：区别于均方差（标准差）！！！标准差，也称均方差，定义为方差的算术平方根，反映组内个体间的离散程度。

                                                                       

均方误差是非负值，模型越好MSE越接近零。

4.均方对数误差（mean squared logarithmic error）

mean_squared_log_error(y_true, y_pred, sample_weight=None, multioutput='uniform_average')

                                                                   

均方对数误差是非负值，模型越好MSLE越接近零。

5.中值绝对误差（median absolute error）

median_absolute_error(y_true, y_pred)

中值绝对误差是非负值，模型越好MSE越接近零。

6.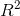决定系数分数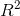（(coefficient of determination) score）

r2_score(y_true, y_pred, sample_weight=None, multioutput='uniform_average')

                                                                   

最佳模型的决定系数分数值为1，常数模型值为0，模型越差值越小。