F - Maximum White Subtree
F - Maximum White Subtree
- 看我博客我有没看懂的地方,或者其他疑问,可以加我qq和我交流~我会及时解答
- qq:1244536605(加好友时备注一下 博客 哈)
标签
- 换根dp
简明题意
- 给定n个节点的树,每个节点的值为0或1.
- 现在需要你对树的每个节点v求出:包含v的联通子图中,节点1的数量减去0的数量,最多是多少。
思路
- 假如要求的这个点v是根节点,那么我们可以dp,一个值为1的节点,他的值等于他所有子树中,dp为为正数的和。也就是 d p [ u ] = ∑ v = u 的 所 有 儿 子 且 d p [ v ] 为 正 数 d p [ v ] + ( a [ u ] = = 1 ) dp[u]=\sum_{v=u的所有儿子且dp[v]为正数}dp[v]+(a[u]==1) dp[u]=v=u的所有儿子且dp[v]为正数∑dp[v]+(a[u]==1)
- 这里是从下往上的,从叶子节点到根节点,那么可以dfs,或者记忆化搜索。
- 这样下来,我们算出了某个节点的答案,复杂度为O(n)。但一共有n个节点,复杂度就是n方了,无法接受。而这里,我们不需要把每个节点当作根都dp一遍,我们可以换根dp。
- 假设我们先以1号节点为根,dp了一遍。那么dp[i]表示的是节点i的子树中,1的数量和0的数量最大的差值。现在看这个图

- 假设现在需要计算包含5号节点的最大差值。那么我们可以把这棵树分成两个部分:
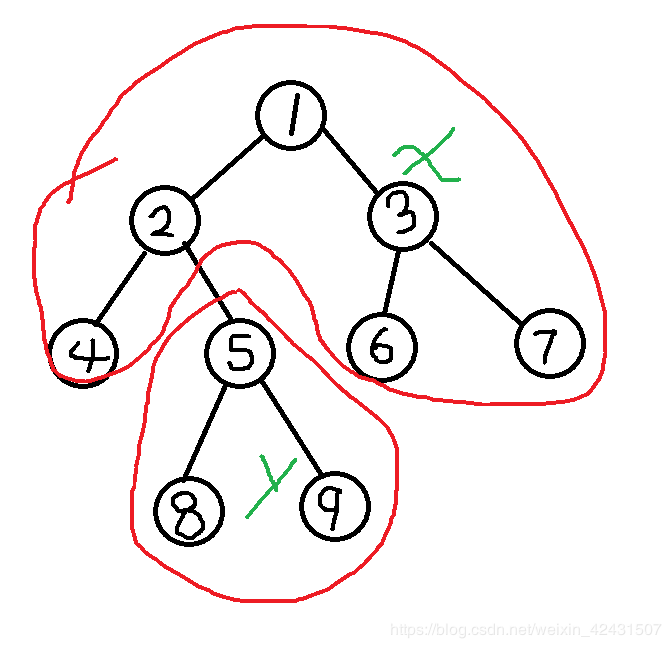
- 我们令f(x)表示包含x的最大差值。现在计算f(5),用x、y标出了这两个部分。我们发现y部分,就等于dp[5],那么dp[5]>0就累加进f(5)。再看x部分。
- 求x部分,可不可以直接用dp[1]-dp[5]?不可以,因为你不知道y这一部分有没有贡献到f(1)中,即使知道f(5)的正负。比如2和3,它们是1的儿子,那么dp[2]和dp[3]可以确定是否贡献到dp[1]中,也就是只要儿子的dp[]值是正数,那么可以贡献到父节点中。而5和1的关系是孙子。孙子是不一定能贡献到爷爷的。举个例子吧,比如2和5节点之间有100个值为0的,那么y部分就算全部是1也不可能贡献进dp[1].
- 所以我们算x部分的时候,应该从y部分的根节点考虑。也就是从5号节点考虑。我们只能知道5号节点能不能给他的父亲2号节点贡献。考虑到这里,就很容易算了,用f(2)-max(dp[5],0)即可。也就是如果dp[5]>0那么它是贡献进了f(2)的,那么就需要减去。否则没有贡献进去,就不需要减去。
- 所以f的递归式是这样的:
f ( u ) = d p [ u ] + m a x ( x , 0 ) f(u)=dp[u]+max(x,0) f(u)=dp[u]+max(x,0)
其中
x = f ( f a [ u ] ) − m a x ( d p [ 5 ] , 0 ) x=f(fa[u])-max(dp[5],0) x=f(fa[u])−max(dp[5],0) - 先树形dp,再换根dp
- 这里注意一点,x部分要判断正负以决定是否加入贡献。而x部分,不需要考虑正负,直接贡献。因为,我们求的f(u)一定是包含u的。那么dp[u]就刚好包含u了。
注意事项
- 无
总结
- 题目询问多个答案,如果每个答案都要以各自的根求出来,那么我们要考虑换根dp
AC代码
#include
#include
#include
#include
#include
#include