Python信号处理：快速傅里叶变换(FFT)，短时傅里叶变换(STFT)，窗函数，以及滤波

摘要：一直以来都是用MATLAB做信号处理，得到预处理的特征后再用Python进一步应用神经网络之类的方法。这里将MATLAB中的FFT、STFT、加窗以及带通滤波通过Python接口实现，防止以后MATLAB用不了了，一定程度上也提高了效率，不用两个软件换来换去。

系列目录

1. Python信号处理：快速傅里叶变换(FFT)，短时傅里叶变换(STFT)，窗函数，以及滤波
2. Python信号处理：自相关函数(对标MATLAB中的autocorr)
3. Python信号处理：波束形成及目标方位估计，CBF、MVDR
4. Python信号处理：cvxpy工具包求解稀疏约束优化问题

目录

1. 快速傅里叶变换(FFT)
2. 窗函数对傅里叶变换的影响
3. 两种信号滤波方式
4. 短时傅里叶变换(STFT)

1. 快速傅里叶变换

FFT的实现主要有两种方法，分别通过np.fft或scipy.fftpack中的fft实现，实现方法基本是一样的，以scipy.fftpack.fft为例。

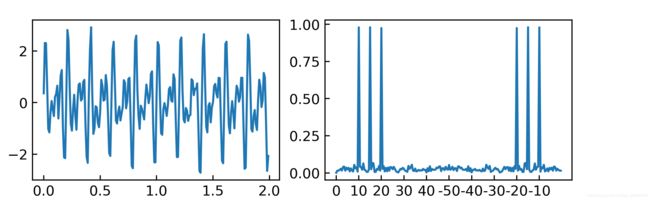
首先生成一个带噪声的信号，频率为10、15、20 Hz，采样率$f_s$=100 Hz，时长2 s。时域波形如下左图所示。使用scipy.fftpack.fft获取频域信号，同时使用scipy.fftpack.fftfreq获取，信号频谱如下右图所示。

X = fftpack.fft(x)           # x为时域信号
freqs = fftpack.fftfreq(N) * fs  # N为信号点数，fs为采样率

2. 窗函数对傅里叶变换的影响

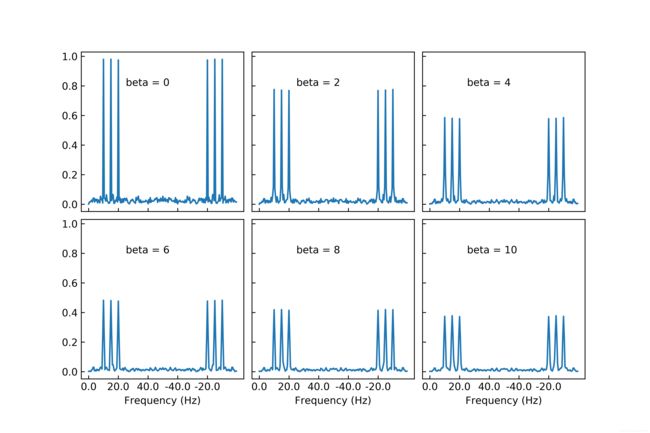
以凯撒窗np.kaiser(点数，系数)为例，凯撒窗能抑制旁瓣，但会加宽主瓣。使用时，在fft中对信号加窗即可。下图给出不同系数的凯撒窗对主瓣和旁瓣的影响。可以看到，加窗后旁瓣受到抑制，但主瓣变宽。通过调整系数，可以改变凯撒窗的窗口。

X = fftpack.fft(np.kaiser(N, 6) * x)

3. 两种信号滤波方式

A. 通过FFT和IFFT进行滤波

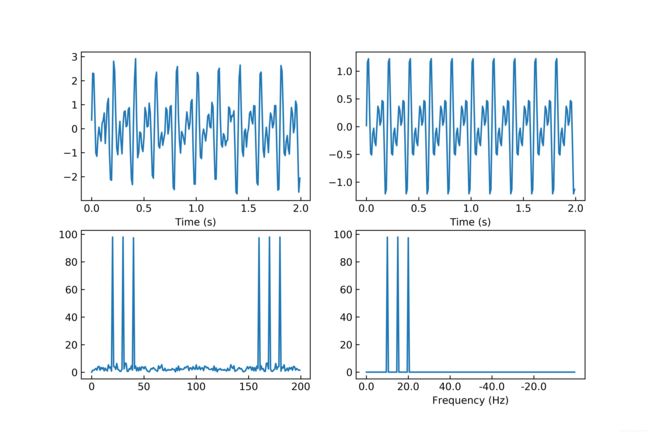
先对信号进行FFT，然后保留想要的频率，将不要的频率都设为0，再将频谱进行IFFT得到滤波后的时域波形。

def filter1(signal, freq, freqs):
    """利用FFT进行滤波。
    # Arguments
    #   signal: 带噪声的时域信号
    #   freq: 想要的频率
    #   freqs: 信号频率
    # Return
    #   y: 滤波后的时域信号
    """
    X = fftpack.fft(signal)
    index_freq = [np.where(i == freqs)[0][0] for i in freq]
    index_zeros = np.setdiff1d(np.arange(0, len(freqs)), index_freq)
    X[index_zeros] = 0
    y = fftpack.ifft(X)
    return y

y = filter1(x, [10, 15, 20], freqs)

滤波后的时域信号及其频谱如下图所示。

B. 通过butter和filtfilt进行滤波

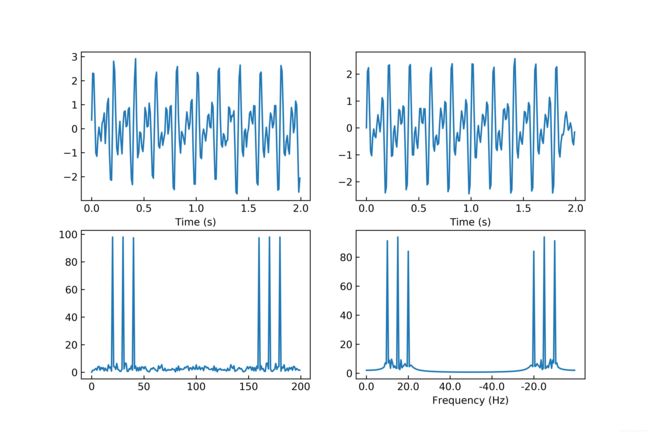
使用scipy.signal.butter通过截至频率获取滤波器系数，利用scipy.signal.filtfilt进行滤波。假设频率为10、15、20 Hz，采样率$f_s$=100 Hz，时长2 s的时域信号，截止频率为10和20 Hz。

wl = 2 * (10 - 1) / fs
wh = 2 * (20 + 1) / fs
b, a = signal.butter(8, [wl ,wh], 'bandpass')  #8表示滤波器的阶数
filtedData = signal.filtfilt(b, a, x)

滤波后的时域信号及其频谱如下图所示。

4. 短时傅里叶变换

有scipy.signal.stft和scipy.signal.spectrogram两个类似的方法，区别在于后者返回的是能量，前者返回的是频谱，差一个绝对值的平方。

两者接口参数如下：

• scipy.signal.stft（x，fs=1.0，window='hann'，nperseg=256，noverlap=None，nfft=None，detrend=False，return_onesided=True，boundary ='zeros'，padded=True，axis=-1 ）

• scipy.signal.spectrogram(x, fs=1.0, window=('tukey', 0.25), nperseg=None, noverlap=None, nfft=None, detrend=’constant’, return_onesided=True, scaling=’density’, axis=-1, mode=’psd’)

常用参数从左往右依次为：信号、采样率、窗、每段长度、重叠长度、FFT点数、消除趋势，两者基本都是一样的。