python中numpy库的使用举例
1、矩阵的创建
1.1 利用np.array()创建一个矩阵,注意array()里面是一个python列表或者元组
1.2 利用np.zeros()创建矩阵
1.3 利用np.ones()创建矩阵
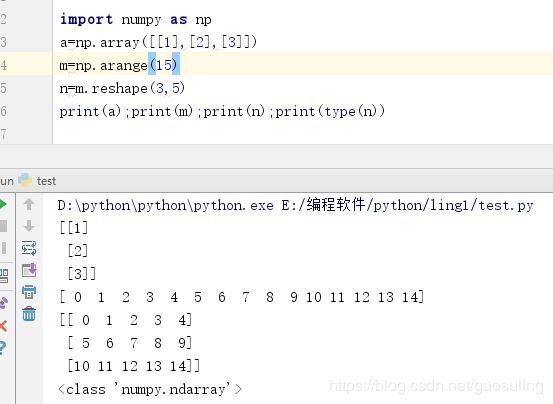
1.4 利用np.arange()创建矩阵
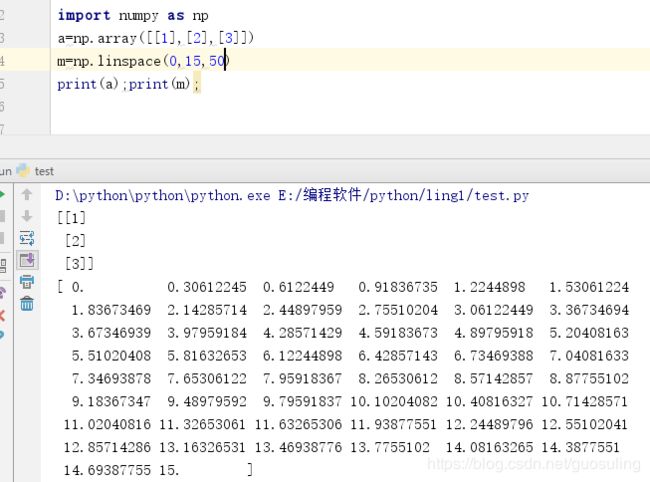
1.5 利用np.linspace()创建矩阵
np.linspace()的作用和np.arange()类似,但是略有不同
np.arange(begin, end, step)中指定起始区间,和步长,np.linspace(begin, end, num)中指定起始起始区间和需要取的数字。
2 矩阵的基本属性
2.1 导入numpy库
2.2、python下numpy元素的类型
2.3 ndarray.ndim 函数,求解矩阵的维数
2.4 ndarray.shape 函数,求解矩阵的规模
2.5 ndarray.size 函数,返回矩阵元素的个数,等于ndarray.shape元素之积
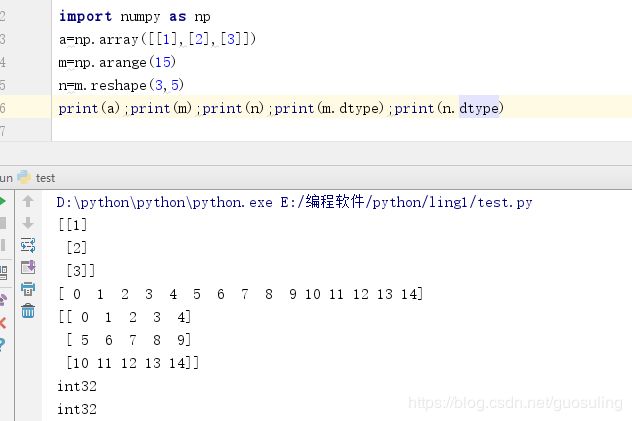
2.6 ndarray.dtype 函数,返回矩阵中元素的类型
类型可以是自己创建的类型或者是标准的python类型,在Numpy中也有自己的类型,有numpy.int32, numpy.int16, numpy.float64等等类型
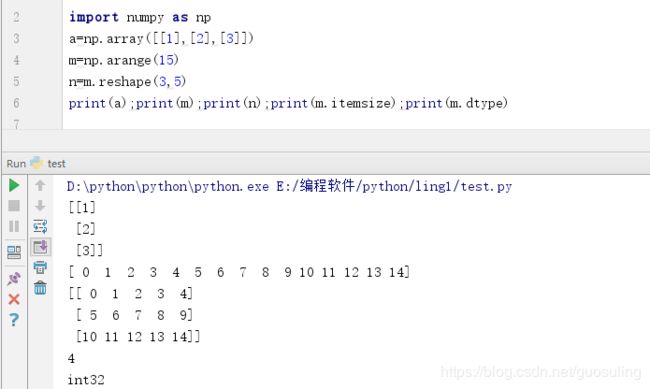
2.7 ndarray.itemsize函数,返回矩阵中每个元素所占的字节数
如同C语言中的sizeof(int)所占4个字节,ndarray.dtype表示当前元素的类型为int32,因此占32/8=4个字节
2.8 ndarray.data 返回矩阵在内存中的具体信息
3、矩阵的基本运算
3.1 矩阵的加法、减法和数乘
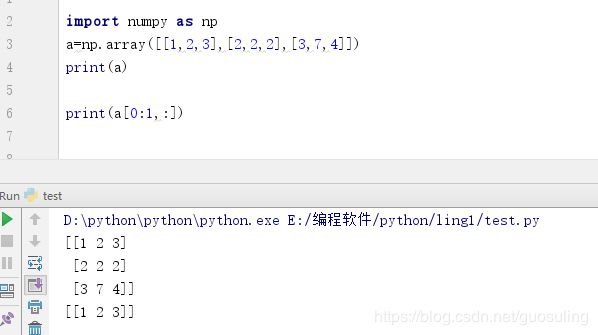
3.2 数组索引
Numpy数组每个元素,每行元素,每列元素都可以用索引访问。
3.3 数组的拷贝
数组的拷贝分浅拷贝和深拷贝两种,浅拷贝通过数组变量的赋值完成,深拷贝使用数组对象的copy方法。
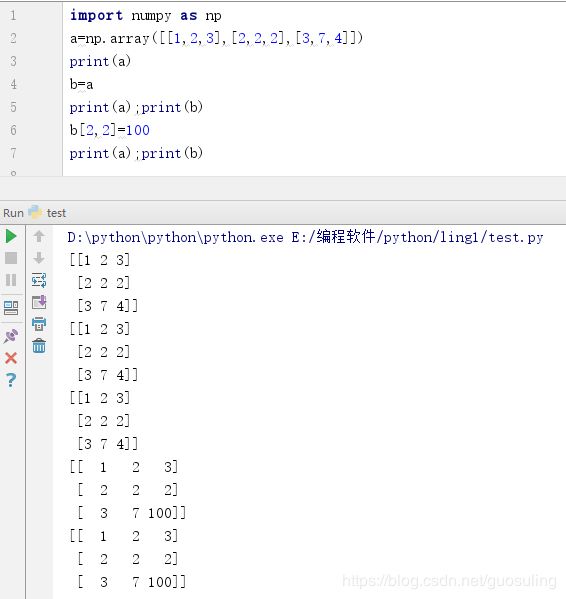
浅拷贝只拷贝数组的引用,如果对拷贝进行修改,源数组也将修改。如下:
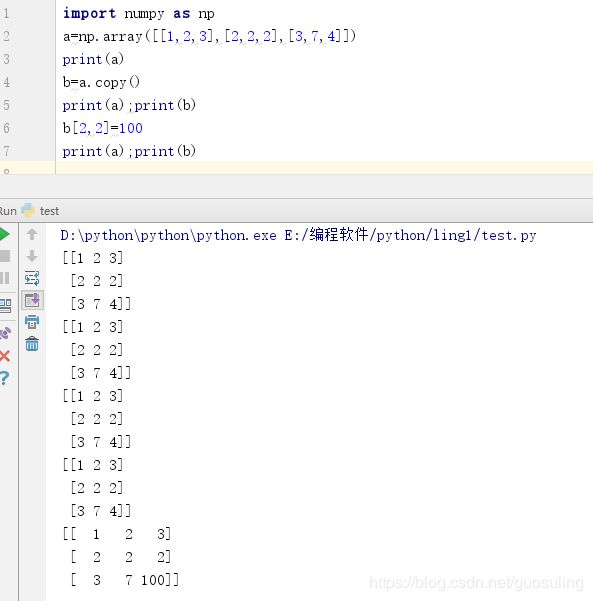
深拷贝会复制一份和源数组一样的数组,新数组与源数组会存放在不同内存位置,因此对新数组的修改不会影响源数组。如下:
4、Numpy线性代数相关函数
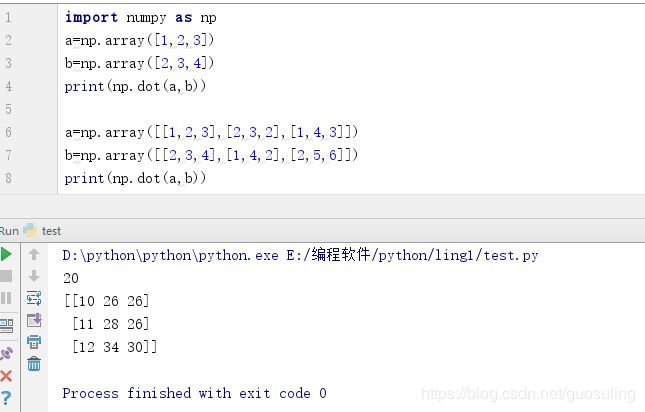
4.1 numpy.dot()
此函数返回两个数组的点积。 对于二维向量,其等效于矩阵乘法。 对于一维数组,它是向量的内积。 对于 N 维数组,它是a的最后一个轴上的和与b的倒数第二个轴的乘积
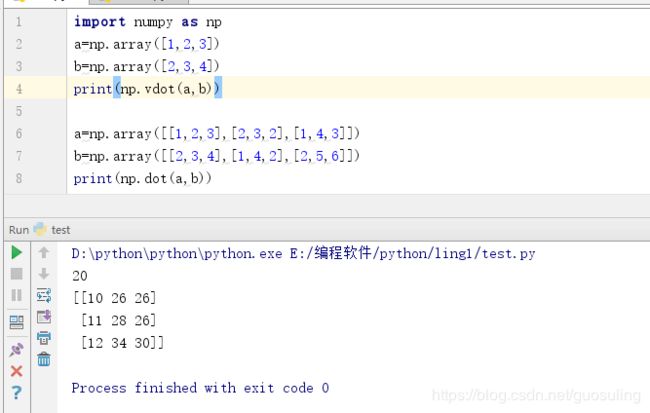
4.2 numpy.vdot()
此函数返回两个向量的点积。 如果第一个参数是复数,那么它的共轭复数会用于计算。 如果参数id是多维数组,它会被展开。
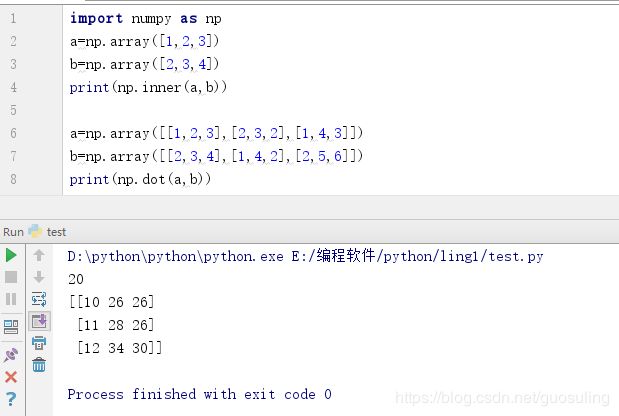
4.3 numpy.inner()
此函数返回一维数组的向量内积。 对于更高的维度,它返回最后一个轴上的和的乘积。
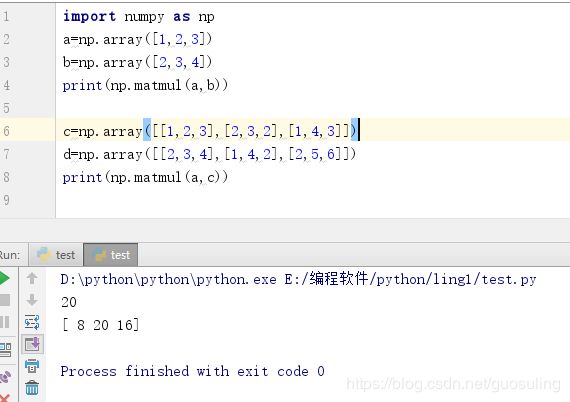
4.4 numpy.matmul()
函数返回两个数组的矩阵乘积。 虽然它返回二维数组的正常乘积,但如果任一参数的维数大于2,则将其视为存在于最后两个索引的矩阵的栈,并进行相应广播。另一方面,如果任一参数是一维数组,则通过在其维度上附加 1 来将其提升为矩阵,并在乘法之后被去除。
4.5 numpy.linalg.det()
行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵,它是左上和右下元素的乘积与其他两个的乘积的差
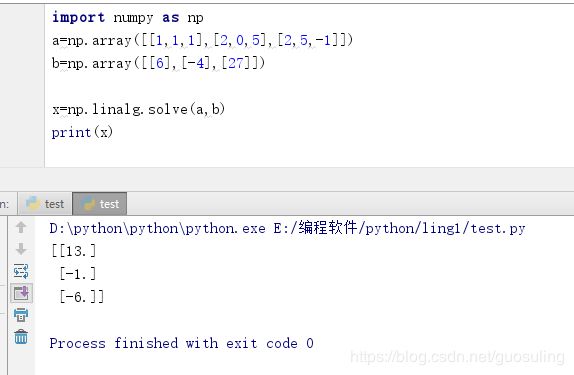
4.6 numpy.linalg.solve()
该函数给出了矩阵形式的线性方程的解。
可表示为AX=B 即求X=A^(-1)B 逆矩阵可以用numpy.linalg.inv()函数来求
注意:*执行的是点乘,对应点相乘,而dot是矩阵乘法
计算线性方程的解
更详细的可参见https://blog.csdn.net/xjl271314/article/details/80409034