机器学习—numpy、matplotlib和sklearn
2.3 numpy库
numpy是高性能的科学计算库。
在numpy中,引入了”ndarray”多维数组的概念,其一维数组表示向量;二维数组表示矩阵,numpy的优势就是包含了矩阵相关的运算。
2.3.1 numpy.ndarray基本属性
#程序2-3
import numpy as np
print(np.__version__)
a = np.array([0,1,2,3,4,5,6,7,8,9])
print(a)
print(type(a))
print('向量a的维数:',a.ndim)
print('向量a的元素(行、列)数:',a.shape)
print('向量a中元素的个数:',a.size)
print('向量a中元素的数据类型:',a.dtype)
print('向量a中每个元素的字节数:',a.itemsize)
b = np.array([[0,1,2,4],[4,5,6,7],[8,9,10,11.0]])
print(b)
print(type(b))
print('矩阵b的维数:',b.ndim)
print('矩阵b的行、列数:',b.shape)
print('矩阵b中元素的个数:',b.size)
print('矩阵b中元素的数据类型:',b.dtype)
print('矩阵b中每个元素的字节数:',b.itemsize)
运行结果:
1.16.0
[0 1 2 3 4 5 6 7 8 9]
向量a的维数: 1
向量a的元素(行、列)数: (10,)
向量a中元素的个数: 10
向量a中元素的数据类型: int32
向量a中每个元素的字节数: 4
[[ 0. 1. 2. 4.]
[ 4. 5. 6. 7.]
[ 8. 9. 10. 11.]]
矩阵b的维数: 2
矩阵b的行、列数: (3, 4)
矩阵b中元素的个数: 12
矩阵b中元素的数据类型: float64
矩阵b中每个元素的字节数: 8
在array对象中,ndim表示多维数组的维数,若是向量则为1,矩阵为2。
在array对象中,shape返回一个元组。若是向量,则元组索引0表示向量中元素的个数;若是矩阵,则元素返回矩阵的行数、列数。
在array对象中,size表示多维数组中元素的个数。
在array对象中,dtype表示多维数组中元素的数据类型。
在array对象中,itemsize表示多维数组中每个元素所占的字节数。
2.3.2创建numpy.ndarray
方法1:使用array
#程序2-4
import numpy as np
a = np.array([[1,2,3],[4,5,6]],dtype=int)
print(a)
print(a.dtype)
b = np.array([[1.0,2,3],[4,5,6]],dtype=float)
print(b)
print(b.dtype)
c = np.array(range(10))
print(c)
print(c.dtype)
d = np.array([x*2 for x in range(10)],dtype=float)
print(d)
print(d.dtype)
运行结果:
[[1 2 3]
[4 5 6]]
int32
[[1. 2. 3.]
[4. 5. 6.]]
float64
[0 1 2 3 4 5 6 7 8 9]
int32
[ 0. 2. 4. 6. 8. 10. 12. 14. 16. 18.]
float64
函数numpy.array(object, dtype = None, copy = True, order = None, subok = False, ndmin = 0),其返回值的数据类型并不是列表,而是numpy.ndarray,数据之间使用空格隔开。
| 参数 |
描述 |
| object |
列表或元组 |
| dtype |
数组元素的数据类型,可选 |
| copy |
对象是否被复制,默认为true,可选 |
| order |
C(按行)、F(按列)、A(任意,默认) |
| subok |
默认情况下,返回的数组被强制为基类数组;如果为true,则返回子类 |
| ndimin |
指定返回数组的最小维数 |
方法2:使用zeros、ones、full
#程序2-5
import numpy as np
a = np.zeros(shape=(2,4))
print(a)
b = np.ones(shape=(3,4),dtype=int)
print(b)
c = np.full(shape=(3,5),fill_value=12,dtype=float)
print(c)
运行结果:
[[0. 0. 0. 0.]
[0. 0. 0. 0.]]
[[1 1 1 1]
[1 1 1 1]
[1 1 1 1]]
[[12. 12. 12. 12. 12.]
[12. 12. 12. 12. 12.]
[12. 12. 12. 12. 12.]]
函数def zeros(shape, dtype=float, order='C')的作用是创建numpy.ndarray数组,其元素填充0;函数def ones(shape, dtype=None, order='C')在数组中填充1;函数def full(shape, fill_value, dtype=None, order='C')在数组中填充fill_value值。
方法3:使用arange
在Python3中可以使用内置的range函数和列表推导式来创建列表,但是range的参数只能是整数,而不能是浮点数。
在numpy中提供了arange来创建数组,def arange(start, stop, step, dtype)表示生成一个从[start,start+step,start+2*step,...,stop)的数字序列,起步长为 step,其中start、stop和step都可以是浮点数。
#程序2-6
import numpy as np
a = [x for x in range(1,10,2)]
print(a)
b = np.arange(0,1,0.2)
print(b)
运行结果:
[1, 3, 5, 7, 9]
[0. 0.2 0.4 0.6 0.8]
代码中a是列表,b是数据类型为numpy.ndarray的数组。
方法4:使用linspace
#程序2-7
import numpy as np
a = np.linspace(1,10,20)
print(a)
b = np.linspace(start=0,stop=1,num=10)
print(b)
运行结果:
[ 1. 1.47368421 1.94736842 2.42105263 2.89473684 3.36842105
3.84210526 4.31578947 4.78947368 5.26315789 5.73684211 6.21052632
6.68421053 7.15789474 7.63157895 8.10526316 8.57894737 9.05263158
9.52631579 10. ]
[0. 0.11111111 0.22222222 0.33333333 0.44444444 0.55555556
0.66666667 0.77777778 0.88888889 1. ]
在numpy中提供linspace函数,def linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)表示在[start,stop]中等分num份,以数组形式返回。
方法5:使用random
#程序2-8
import random
a = random.random()
print(a)
b = random.randint(0,10)
print(b)
运行结果:
0.4582899552517844
9
在random模块中,random函数表示从0-1之间取随机数,randint(a,b)表示从a-b之间取随机整数。
在numpy中,也提供了属于numpy的random模块。
#程序2-9
import numpy as np
a = np.random.random()
print('a:\n',a)
b = np.random.random(size=4)
print('b:\n',b)
b1 = np.random.random(size=(2,4))
print('b1:\n',b1)
b2 = np.random.rand(2,4)
print('b2:\n',b2)
c = np.random.randint(0,10)
print('c:\n',c)
d = np.random.randint(0,10,size=6)
print('d:\n',d)
e = np.random.randint(0,10,size=(3,5))
print('e:\n',e)
运行结果:
a:
0.9207344322941126
b:
[0.02066962 0.64988011 0.05265515 0.60719892]
b1:
[[0.10445075 0.22480481 0.24241775 0.42798398]
[0.24675379 0.84126946 0.43283146 0.73175104]]
b2:
[[0.73849037 0.51166791 0.69993536 0.94138962]
[0.86137873 0.75368827 0.27708881 0.01204831]]
c:
9
d:
[0 9 6 1 3 1]
e:
[[4 0 5 7 1]
[7 5 9 5 3]
[6 9 5 9 4]]
在np.random中,函数def random(size)表示创建范围[0,1)大小为size的numpy.ndarray数组;若不指定size,则表示创建一个在[0,1]之间的随机浮点数。
在np.random中,函数def rand(d0, d1, ..., dn)表示创建一个在[0,1)之间的向量或矩阵。
在np.random中,函数def randint(low, high, size, dtype)表示创建范围是[low,high]、大小为size的numpy.ndarray数组;若不指定size,则表示创建一个在[low,high]之间的随机整数。注:dtype只能是int。
#程序2-10
import numpy as np
#生成特定的随机数与seed(1)相关
np.random.seed(1)
a = np.random.randint(0,10,size=(2,4))
print(a)
#生成特定的随机数与seed(1)相关
np.random.seed(1)
b = np.random.randint(0,10,size=(2,4))
print(b)
#生成特定的随机数与seed(1)相关
np.random.seed(1)
c = np.random.randint(0,10,size=(2,5))
print(c)
运行结果:
[[5 8 9 5]
[0 0 1 7]]
[[5 8 9 5]
[0 0 1 7]]
[[5 8 9 5 0]
[0 1 7 6 9]]
在np.random中,函数seed()表示生成随机种子,即下次生成的随机数和上次使用随机种子生成的随机数相同。
#程序2-11
import numpy as np
a = np.random.normal()
print(a)
b = np.random.normal(1,2,size=(2,4))
print(b)
运行结果:
-0.0541408684419456
[[ 0.0074705 2.7463109 -3.77595745 -0.56081129]
[-0.32193347 -0.08288014 -0.91940303 0.26277848]]
在np.random中,函数def normal(loc=0.0, scale=1.0, size=None)表示生成符合正态分布的随机数,即期望loc是0,标准差scale是1的随机数,size表示数组的大小。
2.3.3 numpy的基本操作
基本操作1:切片
#程序2-12
import numpy as np
a = np.array([0,2,4,6,8,10,12,14,16,18])
# A = np.array([[1,2,3],[4,5,6],[7,8,9]])
print(a)
#索引单位为1的切片
print('正向索引')
print(a[0])
print(a[0:4])
print(a[:4])
print(a[4:])
print('反向索引')
print(a[-1])
print(a[-5:-1])
print(a[-5:])
print(a[:-1])
#索引单位为步长的切片
print('步长')
print(a[0:4:2])
print(a[4:0:-2])
print(a[::-1])
运行结果:
[ 0 2 4 6 8 10 12 14 16 18]
正向索引
0
[0 2 4 6]
[0 2 4 6]
[ 8 10 12 14 16 18]
反向索引
18
[10 12 14 16]
[10 12 14 16 18]
[ 0 2 4 6 8 10 12 14 16]
步长
[0 4]
[8 4]
[18 16 14 12 10 8 6 4 2 0]
在numpy.ndarray数组中的切片操作和列表一致,其索引值都是左闭右开;当步长为正时,正向索引,步长为负时,反向索引。
#程序2-13
import numpy as np
A = np.array([[0,2,4,6,8],[6,8,10,12,14],[12,14,16,18,20],[18,20,22,24,26]])
print(A)
print(A[:2,:2])
print(A[1:,1:])
print(A[:4:2,:5:2])
print(A[::-1,::-1])
运行结果:
[[ 0 2 4 6 8]
[ 6 8 10 12 14]
[12 14 16 18 20]
[18 20 22 24 26]]
[[0 2]
[6 8]]
[[ 8 10 12 14]
[14 16 18 20]
[20 22 24 26]]
[[ 0 4 8]
[12 16 20]]
[[26 24 22 20 18]
[20 18 16 14 12]
[14 12 10 8 6]
[ 8 6 4 2 0]]
在矩阵中进行切片操作,对行切片和对列切片需要使用逗号隔开。
基本操作2:引用和copy
numpy.ndarray数组是引用数据类型,其赋值或切片只是对原数组的引用;因此需要使用copy来进行拷贝。
#程序2-14
import numpy as np
A = np.array([[0,2,4,6,8],[6,8,10,12,14],[12,14,16,18,20],[18,20,22,24,26]])
print(A)
B = A[:4:2,:5:2]
print(B)
B[0,0] = 1000
print(A)
print(B)
运行结果:
[[ 0 2 4 6 8]
[ 6 8 10 12 14]
[12 14 16 18 20]
[18 20 22 24 26]]
[[ 0 4 8]
[12 16 20]]
[[1000 2 4 6 8]
[ 6 8 10 12 14]
[ 12 14 16 18 20]
[ 18 20 22 24 26]]
[[1000 4 8]
[ 12 16 20]]
#程序2-15
import numpy as np
A = np.array([[0,2,4,6,8],[6,8,10,12,14],[12,14,16,18,20],[18,20,22,24,26]])
print(A)
B = A[:4:2,:5:2].copy()
print(B)
B[0,0] = 1000
print(A)
print(B)
运行结果:
[[ 0 2 4 6 8]
[ 6 8 10 12 14]
[12 14 16 18 20]
[18 20 22 24 26]]
[[ 0 4 8]
[12 16 20]]
[[ 0 2 4 6 8]
[ 6 8 10 12 14]
[12 14 16 18 20]
[18 20 22 24 26]]
[[1000 4 8]
[ 12 16 20]]
基本操作3:reshape进行维度变换
#程序2-16
import numpy as np
a = np.array([0,2,4,6,8,10,12,14,16,18])
b = a.reshape(2,5)
c = a.reshape(1,10)
d = a.reshape(10,1)
#-1表示自适应
e = a.reshape(5,-1)
f = a.reshape(-1,2)
print(a)
print(b)
print(c)
print(d)
print(e)
print(f)
运行结果;
[ 0 2 4 6 8 10 12 14 16 18]
[[ 0 2 4 6 8]
[10 12 14 16 18]]
[[ 0 2 4 6 8 10 12 14 16 18]]
[[ 0]
[ 2]
[ 4]
[ 6]
[ 8]
[10]
[12]
[14]
[16]
[18]]
[[ 0 2]
[ 4 6]
[ 8 10]
[12 14]
[16 18]]
[[ 0 2]
[ 4 6]
[ 8 10]
[12 14]
[16 18]]
需要注意的是,a是向量,而c是矩阵。
2.3.4 numpy的合并和分割
#合并1:vstack和hstack
#程序2-17
import numpy as np
A = np.array([[1,2,3],[4,5,6]])
a1 = np.array([7,8,9])
a2 = np.full((2,2),100)
print('A:\n',A)
print('a1:\n',a1)
print('a2:\n',a2)
B = np.vstack([A,a1])
print('B:\n',B)
#B1 = np.vstack([A,A])
B1 = np.vstack([A]*2)
print('B1:\n',B1)
C = np.hstack([A,a2])
print('C:\n',C)
运行结果:
A:
[[1 2 3]
[4 5 6]]
a1:
[7 8 9]
a2:
[[100 100]
[100 100]]
B:
[[1 2 3]
[4 5 6]
[7 8 9]]
B1:
[[1 2 3]
[4 5 6]
[1 2 3]
[4 5 6]]
C:
[[ 1 2 3 100 100]
[ 4 5 6 100 100]]
函数vstack表示沿着行的方向进行合并;函数hstack表示沿着列的方向进行合并。
#合并2:concatenate
#程序2-18
import numpy as np
A = np.array([[1,2,3],[4,5,6]])
a1 = np.array([7,8,9])
a2 = np.full((2,2),100)
print(A)
print(a1)
print(a2)
# B = np.vstack([A,a1])
B = np.concatenate([A,a1.reshape(1,-1)],axis=0)
print(B)
#C = np.hstack([A,a2])
C = np.concatenate([A,a2],axis=1)
print(C)
当函数concatenate的axis等于0时(默认为0),表示沿着行的方向进行合并;axis等于1时,表示沿着列的方向进行合并。
使用vstack和hstack可以在矩阵和向量之间合并,而使用concatenate只能是矩阵和矩阵、向量和向量之间合并。
#分割1:vsplit和hsplit
#程序2-19
import numpy as np
A = np.arange(24).reshape(4,6)
print(A)
A1,A2 = np.vsplit(A,[3])
print(A1)
print(A2)
#多次分割
print(np.vsplit(A,[1,3]))
A3,A4 = np.hsplit(A,[3])
print(A3)
print(A4)
运行结果:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]]
[[18 19 20 21 22 23]]
[array([[0, 1, 2, 3, 4, 5]]), array([[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17]]), array([[18, 19, 20, 21, 22, 23]])]
[[ 0 1 2]
[ 6 7 8]
[12 13 14]
[18 19 20]]
[[ 3 4 5]
[ 9 10 11]
[15 16 17]
[21 22 23]]
使用函数vsplit表示沿着行的方向进行分割;使用函数hsplit表示沿着列的方向进行分割。
#分割2:split
#程序2-20
import numpy as np
A = np.arange(24).reshape(4,6)
print(A)
#A1,A2 = np.split(A,[3],axis=0)
A1,A2 = np.split(A,[3])
print(A1)
print(A2)
#多次分割
print(np.split(A,[1,3]))
A3,A4 = np.split(A,[3],axis=1)
print(A3)
print(A4)
运行结果:
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]
[18 19 20 21 22 23]]
[[ 0 1 2 3 4 5]
[ 6 7 8 9 10 11]
[12 13 14 15 16 17]]
[[18 19 20 21 22 23]]
[array([[0, 1, 2, 3, 4, 5]]), array([[ 6, 7, 8, 9, 10, 11],
[12, 13, 14, 15, 16, 17]]), array([[18, 19, 20, 21, 22, 23]])]
[[ 0 1 2]
[ 6 7 8]
[12 13 14]
[18 19 20]]
[[ 3 4 5]
[ 9 10 11]
[15 16 17]
[21 22 23]]
函数split中,axis为0(默认为0)表示沿着行的方向进行分割;axis为1表示沿着列的方向进行分割。
2.3.5 numpy的矩阵运算
(1)简单的算术运算
#程序2-21
import numpy as np
A = np.arange(1,7).reshape(2,3)
print('A:\n',A)
print('A+1:\n',A+1)
print('A-1:\n',A-1)
print('A*2:\n',A*2)
print('A/2:\n',A/2)
print('A%2:\n',A%2)
print('A//2:\n',A//2)
print('A**2:\n',A**2)
#相当于np.power(2,A)
print('2**A:\n',2**A)
print('np.sin(A):\n',np.sin(A))
print('np.log(A):\n',np.log(A))
print('np.abs(A):\n',np.abs(A))
print('np.exp(A):\n',np.exp(A))
#算法运算其返回值不是原数组的引用
print('算术运算和引用')
A1 = A * 2
print('A1:\n',A1)
A1[0,0] = 100
print('A:\n',A)
print('A1:\n',A1)
运行结果:
A:
[[1 2 3]
[4 5 6]]
A+1:
[[2 3 4]
[5 6 7]]
A-1:
[[0 1 2]
[3 4 5]]
A*2:
[[ 2 4 6]
[ 8 10 12]]
A/2:
[[0.5 1. 1.5]
[2. 2.5 3. ]]
A%2:
[[1 0 1]
[0 1 0]]
A//2:
[[0 1 1]
[2 2 3]]
A**2:
[[ 1 4 9]
[16 25 36]]
2**A:
[[ 2 4 8]
[16 32 64]]
np.sin(A):
[[ 0.84147098 0.90929743 0.14112001]
[-0.7568025 -0.95892427 -0.2794155 ]]
np.log(A):
[[0. 0.69314718 1.09861229]
[1.38629436 1.60943791 1.79175947]]
np.abs(A):
[[1 2 3]
[4 5 6]]
np.exp(A):
[[ 2.71828183 7.3890561 20.08553692]
[ 54.59815003 148.4131591 403.42879349]]
算术运算和引用
A1:
[[ 2 4 6]
[ 8 10 12]]
A:
[[1 2 3]
[4 5 6]]
A1:
[[100 4 6]
[ 8 10 12]]
(2)向量和矩阵之间的运算
在数学运算中,向量a乘以矩阵A,则向量a必须是和矩阵A相同列数的行向量;若矩阵A乘以向量a,则向量a必须是和矩阵A相同行数的列向量。
#程序2-22
import numpy as np
A = np.arange(1,7).reshape(2,3)
a1 = np.array([2,2,2])
a2 = np.array([10,10])
print('A:\n',A)
print('a1:\n',a1)
print('a2:\n',a2)
print('A.dot(a1):\n',A.dot(a1))
print('a2.dot(A):\n',a2.dot(A))
运行结果:
A:
[[1 2 3]
[4 5 6]]
a1:
[2 2 2]
a2:
[10 10]
A.dot(a1):
[12 30]
a2.dot(A):
[50 70 90]
在numpy中,还提供很多特殊的向量矩阵运算,虽然这些运算并不符合数学运算中的规则,但是使用起来很方便。numpy中向量和矩阵的特殊运算:+、-、*、/、%、//、**等。
#程序2-23
import numpy as np
A = np.arange(1,7).reshape(2,3)
a1 = np.array([2,2,2])
a2 = np.array([10,10])
print('A:\n',A)
print('a1:\n',a1)
print('a2:\n',a2)
print('A+a1:\n',A+a1)
print('A-a1:\n',A-a1)
print('A*a1:\n',A*a1)
print('A/a1:\n',A/a1)
运行结果:
A:
[[1 2 3]
[4 5 6]]
a1:
[2 2 2]
a2:
[10 10]
A+a1:
[[3 4 5]
[6 7 8]]
A-a1:
[[-1 0 1]
[ 2 3 4]]
A*a1:
[[ 2 4 6]
[ 8 10 12]]
A/a1:
[[0.5 1. 1.5]
[2. 2.5 3. ]]
(3)矩阵和矩阵之间的运算
在数学运算中,矩阵A和矩阵B相加减,则矩阵A和矩阵B必须相同行、列数;矩阵A和矩阵B相乘,则矩阵A的行、列数必须和矩阵B的列、行数对应相等。除此之外,还需要求矩阵的转置和矩阵的逆。
#程序2-24
import numpy as np
A = np.arange(11,17).reshape(2,3)
B = np.full([2,3],10)
print('A:\n',A)
print('B:\n',B)
print('A-B:\n',A-B)
print('A+B:\n',A+B)
C = B.reshape(3,2)
print('C:\n',C)
print('A.dot(C):\n',A.dot(C))
print('A.T:\n',A.T)
D = np.arange(1,5).reshape(2,2)
print('D:\n',D)
print('方阵D的逆矩阵:\n',np.linalg.inv(D))
print(D.dot(np.linalg.inv(D)))
print('非方阵A的伪逆矩阵:\n',np.linalg.pinv(A))
print(A.dot(np.linalg.pinv(A)))
运行结果:
A:
[[11 12 13]
[14 15 16]]
B:
[[10 10 10]
[10 10 10]]
A-B:
[[1 2 3]
[4 5 6]]
A+B:
[[21 22 23]
[24 25 26]]
C:
[[10 10]
[10 10]
[10 10]]
A.dot(C):
[[360 360]
[450 450]]
A.T:
[[11 14]
[12 15]
[13 16]]
D:
[[1 2]
[3 4]]
方阵D的逆矩阵:
[[-2. 1. ]
[ 1.5 -0.5]]
[[1.0000000e+00 0.0000000e+00]
[8.8817842e-16 1.0000000e+00]]
非方阵A的伪逆矩阵:
[[-2.61111111 2.11111111]
[-0.11111111 0.11111111]
[ 2.38888889 -1.88888889]]
[[1.00000000e+00 5.55111512e-15]
[0.00000000e+00 1.00000000e+00]]
在numpy中,还提供很多特殊的矩阵和矩阵之间运算,虽然这些运算并不符合数学运算中的规则,但是使用起来很方便。numpy中矩阵和矩阵的特殊运算:*、/、%、//、**等。
#程序2-25
import numpy as np
A = np.arange(1,7).reshape(2,3)
B = np.full([2,3],10)
print('A:\n',A)
print('B:\n',B)
print('A*B:\n',A*B)
print('A/B:\n',A/B)
print('A%B:\n',A%B)
print('A//B:\n',A//B)
print('A**B:\n',A**B)
运行结果:
A:
[[1 2 3]
[4 5 6]]
B:
[[10 10 10]
[10 10 10]]
[[10 20 30]
[40 50 60]]
[[0.1 0.2 0.3]
[0.4 0.5 0.6]]
[[1 2 3]
[4 5 6]]
[[0 0 0]
[0 0 0]]
[[ 1 1024 59049]
[ 1048576 9765625 60466176]]
2.3.6 numpy的聚合运算
#程序2-26
import numpy as np
A = np.arange(1,7).reshape(2,3)
print('A:\n',A)
print('矩阵A所有元素求和:\n',np.sum(A))
print('矩阵A沿着行方向求元素和:\n',np.sum(A,axis=0))
print('矩阵A沿着列方向求元素和:\n',np.sum(A,axis=1))
print('矩阵A所有元素相乘:\n',np.prod(A))
print('矩阵A的平均值:\n',np.mean(A))
print('矩阵A的中位数:\n',np.median(A))
print('矩阵A的方差:\n',np.var(A))
print('矩阵A的标准差:\n',np.std(A))
print('矩阵A的最小值:\n',np.min(A))
print('矩阵A的最大值:\n',np.max(A))
#numpy.percentile(a, q, axis):计算百分位数
#a:输入数组;q:要计算的百分位数,在0~100之间;axis:沿着它计算百分位数的轴
print('矩阵A在25%的分位数:\n',np.percentile(A,q=25))
print('矩阵A在50%的分位数:\n',np.percentile(A,q=50))
print('矩阵A在75%的分位数:\n',np.percentile(A,q=75))
运行结果:
A:
[[1 2 3]
[4 5 6]]
矩阵A所有元素求和:
21
矩阵A沿着行方向求元素和:
[5 7 9]
矩阵A沿着列方向求元素和:
[ 6 15]
矩阵A所有元素相乘:
720
矩阵A的平均值:
3.5
矩阵A的中位数:
3.5
矩阵A的方差:
2.9166666666666665
矩阵A的标准差:
1.707825127659933
矩阵A的最小值:
1
矩阵A的最大值:
6
矩阵A在25%的分位数:
2.25
矩阵A在50%的分位数:
3.5
矩阵A在75%的分位数:
4.75
注;在numpy的矩阵中,行的方向是从上往下,列的方向是从左向右。
2.3.7 numpy的排序和索引
(1)排序
#程序2-27
import numpy as np
A = np.arange(1,16)
#函数shuffle(X)将X打乱顺序,并存入X
np.random.shuffle(A)
A = A.reshape(3,5)
print('乱序A:\n',A)
#相当于B = np.sort(A,axis=1)
B = np.sort(A)
print('排序B:\n',B)
B1 = np.sort(A,axis=0)
print('排序B1:\n',B1)
#位置排序函数partition
#当axis=0表示沿着行的方向排序,位置0数值为a,位置1数值为b,以此类推
#则a
C = np.partition(A,1,axis=0)
print('C:\n',C)
#当axis=1表示沿着列的方向排序,位置0数值为a,位置1数值为b,以此类推
#则a/b
#相当于C1 = np.partition(A,2)
C1 = np.partition(A,2,axis=1)
print('C1:\n',C1)
运行结果:
乱序A:
[[13 7 15 5 12]
[ 4 6 14 2 10]
[ 3 9 11 8 1]]
排序B:
[[ 5 7 12 13 15]
[ 2 4 6 10 14]
[ 1 3 8 9 11]]
排序B1:
[[ 3 6 11 2 1]
[ 4 7 14 5 10]
[13 9 15 8 12]]
C:
[[ 3 6 11 2 1]
[ 4 7 14 5 10]
[13 9 15 8 12]]
C1:
[[ 5 7 12 13 15]
[ 2 4 6 14 10]
[ 1 3 8 11 9]]
(2)索引
#程序2-28
import numpy as np
A = np.arange(1,16)
#函数shuffle(X)将X打乱顺序,并存入X
np.random.shuffle(A)
A = A.reshape(3,5)
print('乱序A:\n',A)
n1 = np.argmin(A,axis=0)
print('沿着行的方向最小值的索引:',n1)
n2 = np.argmin(A,axis=1)
print('沿着列的方向最小值的索引:',n2)
#相当于A1 = np.argsort(A)
A1 = np.argsort(A,axis=1)
print('沿着列的方向排序的索引:\n',A1)
A2 = np.argsort(A,axis=0)
print('沿着行的方向排序的索引:\n',A2)
#相当于A3 = np.argpartition(A,3)
A3 = np.argpartition(A,3,axis=1)
print('沿着列的方向对位置3大小排序的索引:\n',A3)
A4 = np.argpartition(A,1,axis=0)
print('沿着行的方向对位置1大小排序的索引:\n',A4)
运行结果:
乱序A:
[[ 7 12 15 10 1]
[ 5 13 4 14 11]
[ 3 9 8 6 2]]
沿着行的方向最小值的索引: [2 2 1 2 0]
沿着列的方向最小值的索引: [4 2 4]
沿着列的方向排序的索引:
[[4 0 3 1 2]
[2 0 4 1 3]
[4 0 3 2 1]]
沿着行的方向排序的索引:
[[2 2 1 2 0]
[1 0 2 0 2]
[0 1 0 1 1]]
沿着列的方向对位置3大小排序的索引:
[[4 0 3 1 2]
[2 0 4 1 3]
[4 0 3 2 1]]
沿着行的方向对位置1大小排序的索引:
[[2 2 1 2 0]
[1 0 2 0 2]
[0 1 0 1 1]]
在聚合运算中,其函数的默认axis为0,表示沿着行的方向进行聚合;而在索引和排序运算中,其函数的默认axis为1,表示沿着列的方向索引和排序。
2.3.8 numpy的比较运算
#程序2-29
import numpy as np
A = np.arange(1,16).reshape(3,5)
print('A:\n',A)
print('A>3:\n',A>3)
print('sum(A>3):\n',np.sum(A>3))
print('sum(A>3,axis=0):\n',np.sum(A>3,axis=0))
print('sum(A>3,axis=1):\n',np.sum(A>3,axis=1))
print('(A>3)&(A<9):\n',(A>3)&(A<9))
print('(A>3)|(A>9):\n',(A>3)|(A>9))
print('A!=3:\n',A!=3)
print('~(A==3):\n',~(A==3))
#any函数表示数组中任一一个元素满足条件,返回True
print('any(A!=3):\n',np.any(A!=3))
print('any(A!=3,axis=0):\n',np.any(A!=3,axis=0))
print('any(A!=3,axis=1):\n',np.any(A!=3,axis=1))
#all函数表示只有当数组的所有元组都满足条件,才返回True
print('all(A>0):\n',np.all(A>0))
print('all(A>0,axis=0):\n',np.all(A>0,axis=0))
print('all(A>0,axis=1):\n',np.all(A>0,axis=1))
运行结果:
A:
[[ 1 2 3 4 5]
[ 6 7 8 9 10]
[11 12 13 14 15]]
A>3:
[[False False False True True]
[ True True True True True]
[ True True True True True]]
sum(A>3):
12
sum(A>3,axis=0):
[2 2 2 3 3]
sum(A>3,axis=1):
[2 5 5]
(A>3)&(A<9):
[[False False False True True]
[ True True True False False]
[False False False False False]]
(A>3)|(A>9):
[[False False False True True]
[ True True True True True]
[ True True True True True]]
A!=3:
[[ True True False True True]
[ True True True True True]
[ True True True True True]]
~(A==3):
[[ True True False True True]
[ True True True True True]
[ True True True True True]]
any(A!=3):
True
any(A!=3,axis=0):
[ True True True True True]
any(A!=3,axis=1):
[ True True True]
all(A>0):
True
all(A>0,axis=0):
[ True True True True True]
all(A>0,axis=1):
[ True True True]
numpy的比较运算中,其比较条件使用位运算进行合并。
2.3.9 fancy indexing
(1)向量的fancy indexing中,其[ ]内只有一个参数,表示对向量的索引。
#程序2-30
import numpy as np
a = np.arange(1,10)
print('a:\n',a)
#fancy indexing
print('a[[3,5,7]]:\n',a[[3,5,7]])
#ind必须是numpy数组
ind = np.array([[3,5],[1,7]])
print('ind:\n',ind)
print('a[ind]:\n',a[ind])
print('a[a<4]:\n',a[a<4])
运行结果:
a:
[1 2 3 4 5 6 7 8 9]
a[[3,5,7]]:
[4 6 8]
ind:
[[3 5]
[1 7]]
a[ind]:
[[4 6]
[2 8]]
a[a<4]:
[1 2 3]
(2)矩阵的fancy indexing中,[ ]内有两个参数,第一个参数表示对矩阵行的索引,第二个参数表示对矩阵列的索引。
#程序2-31
import numpy as np
A = np.arange(1,13).reshape(4,3)
print('A:\n',A)
#fancy indexing
row = np.array([0,2,3])
print('row:\n',row)
col = np.array([0,1,2])
print('col:\n',col)
#索引矩阵中具体的值
print('A[row,col]:\n',A[row,col])
print('A[[0,2,3],[0,1,2]]:\n',A[[0,2,3],[0,1,2]])
print('A[2,0]:\n',A[2,0])
print('A[2,0:2]:\n',A[2,0:2])
#索引矩阵中符合条件的部分矩阵
print('A[:3,1:]:\n',A[:3,1:])
print('A[:3,[1,2]]:\n',A[:3,[1,2]])
print('A[A[:,1]%2==0,:]:\n',A[A[:,1]%2==0,:])
#索引矩阵中bool为True的向量对应的值
b_row = [True,False,False,True] #必须是向量
print('b_row:\n',b_row)
print('A[b_row,1]:\n',A[b_row,1])
print('A[b_row,1:]:\n',A[b_row,1:])
运行结果:
A:
[[ 1 2 3]
[ 4 5 6]
[ 7 8 9]
[10 11 12]]
row:
[0 2 3]
col:
[0 1 2]
A[row,col]:
[ 1 8 12]
A[[0,2,3],[0,1,2]]:
[ 1 8 12]
A[2,0]:
7
A[2,0:2]:
[7 8]
A[:3,1:]:
[[2 3]
[5 6]
[8 9]]
A[:3,[1,2]]:
[[2 3]
[5 6]
[8 9]]
A[A[:,1]%2==0,:]:
[[1 2 3]
[7 8 9]]
b_row:
[True, False, False, True]
A[b_row,1]:
[ 2 11]
A[b_row,1:]:
[[ 2 3]
[11 12]]
需要注意的是,当fancy indexing和bool序列一起使用时,bool序列必须是一维数组,即向量。
2.4 matplotlib库
2.4.1折线图
#程序2-32
#import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0,10,0.1)
sinx = np.sin(x)
cosx = np.cos(x)
#设置颜色、线条样式、线条标签
#b:blue;g:green;r:red;c:cyan;m:magenta;y:yellow;k:black;w:white
#linestyle类别':'、'-.'、'--'、'-'
plt.plot(x,sinx,color='blue',linestyle='-',label='y=sin(x)')
plt.plot(x,cosx,color='r',linestyle='-.',label='y=cos(x)')
#显示图例(图的标签)
plt.legend()
#设置x、y轴上下限
#或plt.axis([-1,11,-1.1,1.1])
plt.xlim(-1,11)
plt.ylim(-1.1,1.1)
#设置标题、x、y轴标签
plt.title('learn matplotlib')
plt.xlabel('x-lable')
plt.ylabel('y-lable')
#显示图像
plt.show()
运行结果:
还可以将两个图片分开绘制。
#程序2-33
#import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0,10,0.1)
sinx = np.sin(x)
cosx = np.cos(x)
#subplot(numRows,numCols,plotNum)
#整个Figure会被划分为numRows行,numCols列,并从左往右
#plotNum指定了子图所在的位置,即子图编号
#绘制子图1
plt.subplot(2,1,1)
#设置颜色、线条样式、线条标签
plt.plot(x,sinx,color='blue',linestyle='-',label='y=sin(x)')
#显示图例(图的标签)
plt.legend()
#设置x、y轴上下限
#或plt.axis([-1,11,-1.1,1.1])
plt.xlim(-1,11)
plt.ylim(-1.1,1.1)
#设置标题、x、y轴标签
plt.title('learn matplotlib')
plt.ylabel('y-lable')
#绘制子图2
plt.subplot(2,1,2)
#设置颜色、线条样式、线条标签
plt.plot(x,cosx,color='r',linestyle='-.',label='y=cos(x)')
#显示图例(图的标签)
plt.legend()
#设置x、y轴上下限
#或plt.axis([-1,11,-1.1,1.1])
plt.xlim(-1,11)
plt.ylim(-1.1,1.1)
#设置标题、x、y轴标签
plt.xlabel('x-lable')
plt.ylabel('y-lable')
#显示图像
plt.show()
运行结果:
2.4.2散点图
#程序2-34
#import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(0,10,0.4)
sinx = np.sin(x)
cosx = np.cos(x)
#subplot(numRows,numCols,plotNum)
#整个Figure会被划分为numRows行,numCols列,并从左往右
#plotNum指定了子图所在的位置,即子图编号
#绘制子图1
plt.subplot(2,1,1)
#设置颜色、点标签、点样式(marker)、点透明度(alpha)
plt.scatter(x,sinx,color='blue',label='y=sin(x)',marker='+',alpha=0.5)
#显示图例(图的标签)
plt.legend()
#设置x、y轴上下限
#或plt.axis([-1,11,-1.1,1.1])
plt.xlim(-1,11)
plt.ylim(-1.1,1.1)
#设置标题、x、y轴标签
plt.title('learn matplotlib')
plt.ylabel('y-lable')
#绘制子图2
plt.subplot(2,1,2)
#设置颜色、点标签、点样式(marker)、点透明度(alpha)
plt.scatter(x,cosx,color='r',label='y=cos(x)',marker='.',alpha=0.5)
#显示图例(图的标签)
plt.legend()
#设置x、y轴上下限
#或plt.axis([-1,11,-1.1,1.1])
plt.xlim(-1,11)
plt.ylim(-1.1,1.1)
#设置标题、x、y轴标签
plt.xlabel('x-lable')
plt.ylabel('y-lable')
#显示图像
plt.show()
运行结果:
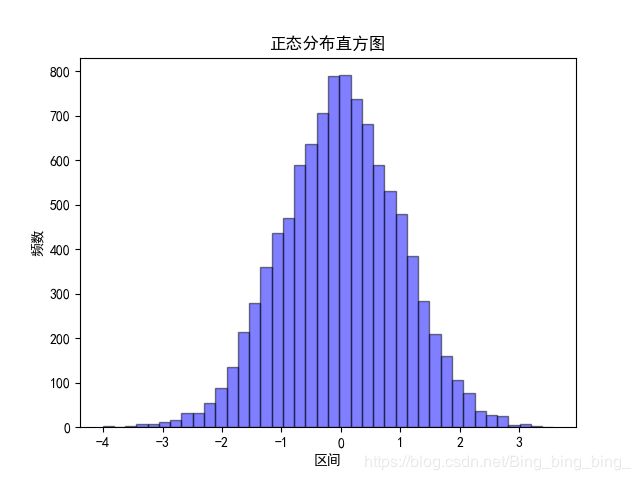
2.4.3直方图
#程序2-35
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
#rcParams是matplotlib的配置参数
#使用matplotliblib画图的时候经常会遇见中文或者是负号无法显示的情况
mpl.rcParams['font.sans-serif']=['SimHei'] #用黑体显示中文
mpl.rcParams['axes.unicode_minus']=False #正常显示负号
# 随机生成10000个服从正态分布的数据
data = np.random.randn(10000)
"""
使用hist()函数绘制直方图
data:必选参数,绘图数据
bins:直方图的长条形数目,可选项,默认为10
density:是否将得到的直方图向量归一化,可选项;
density默认为0,代表不归一化,显示频数;density=1,表示归一化,显示频率
facecolor:长条形的颜色
edgecolor:长条形边框的颜色
alpha:透明度
"""
plt.hist(data, bins=40, density=0, facecolor="b", edgecolor="k", alpha=0.5)
#显示横轴标签
plt.xlabel("区间")
#显示纵轴标签
plt.ylabel("频数")
#显示图标题
plt.title("正态分布直方图")
plt.show()
运行结果:
2.5 sklearn库
#程序2-36
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets
iris = datasets.load_iris()
'''
data:鸢尾花数据集的特征集(150,4)
target:鸢尾花数据集的标签集(150,)
target_names:鸢尾花标签对应的名称['setosa' 'versicolor' 'virginica']
DESCR:鸢尾花数据集的说明文档
feature_names:鸢尾花特征对应的名称,
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
filename:数据集存放的位置,
D:\Program Files (x86)\Python\lib\site-packages\sklearn\datasets\data\iris.csv
'''
print(iris.keys())
X = iris.data[:,2:]
y = iris.target
plt.scatter(X[y==0,0],X[y==0,1],color='blue',label='setosa',marker='+',alpha=0.5)
plt.scatter(X[y==1,0],X[y==1,1],color='red',label='versicolor',marker='.',alpha=0.5)
plt.scatter(X[y==2,0],X[y==2,1],color='black',label='virginica',marker='*',alpha=0.5)
plt.legend()
plt.xlabel('petal length (cm)')
plt.ylabel('petal width (cm)')
plt.title('iris dataset')
plt.show()
运行结果: