EWAHCompressedBitmap数据结构及原理
- EWAH 意思是 Enhanced Word-Aligned Hybrid,在WAH基础上优化而来。
- EWAH 算法论文:《Sorting improves word-aligned bitmap indexes》
- javaewah项目(Java版)GitHub地址:https://github.com/lemire/javaewah
- EWAHBoolArray项目(C++版) GitHub地址:https://github.com/lemire/EWAHBoolArray
本文基于Java版项目javaewah。
首先
首先要知道,EWAHCompressedBitmap是完全基于行程压缩算法压缩的。
结构就是这样,看起来很简单。
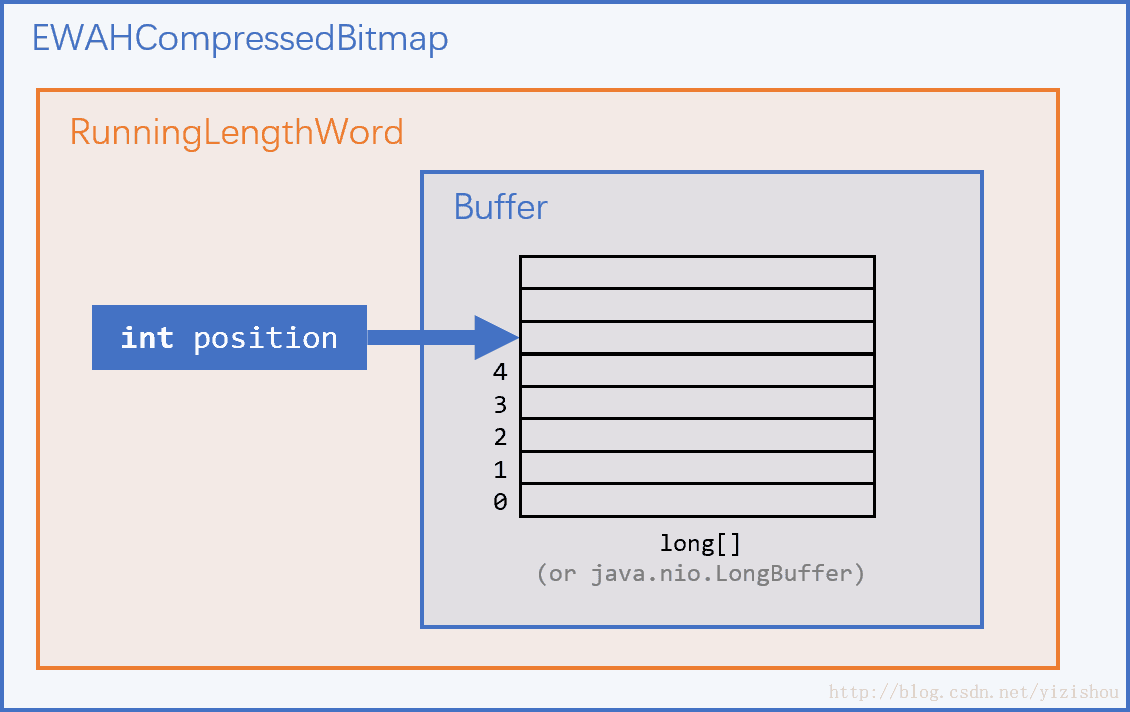
在构造EWAHCompressedBitmap时,内部会初始化一个RunningLengthWord,来存储EWAH压缩算法必需的两个数据结构:
/**
* The array of words.
*/
final Buffer buffer;
/**
* The position in array.
*/
int position;其中Buffer根据实现的不同可能是
- LongArray,内部为
long[],使用默认构造方法构造Bitmap时就会构造LongArray - LongBufferWrapper, 内部为
java.nio.LongBuffer,这样可以直接使用NIO的特性。在使用java.nio.ByteBuffer构造Bitmap时会构造LongBufferWrapper
不管什么实现,我们把Buffer直接理解为存储了一堆long的数组即可。
RunningLengthWord
RunningLengthWord存储了EWAHCompressedBitmap的全部数据,是整个项目中的核心。
其原理为:
将整个(未经过任何压缩的)bitmap每64位拆分为一个最小单元(long),只可能出现两种情况:
- 64位全都是相同的比特,要么全都是1,要么全都是0,这样的数据可以被run-length压缩。尤其是当这种情况发生在连续的多个long上的时候,压缩效果更为明显。
- 64位范围内既有0又有1,这样的数据不进行压缩,而是直接存储字面量,这样的数据在论文中叫做Dirty Word,生动形象。其实如果整个bitmap中大量出现Dirty Word的话,压缩效果会大打折扣。
根据上面的原理,RunningLengthWord使用了这样的实现:
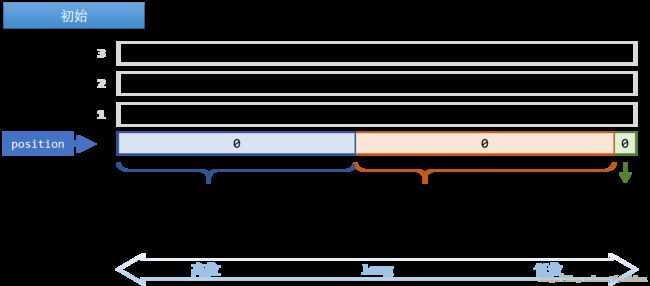
如果所示,在初始化时,Buffer中下标为0的位置一定是一个run-length,其64位被拆分成了三部分:
- 最低位(Running Bit):表示当前的run-length压缩的是0还是1。
- 中间32位(Running Length): 表示当前的run-length压缩了几个64位(
long)的连续相同bit。如果这个部分值为0,那么最低位的取值没有实际意义。 - 高31位(Number of Literal Words ):表示当前run-length后面紧接着未压缩的字面量(Dirty Words)的数量。
如果Buffer中下标为N的位置为run-length,且其高位31位表示的Number of Literal Words为2,则Buffer中下标为N+1和N+2的两个位置一定是字面量。
另外有一个性能相关的措施,就是设置一个position,始终指向整个Buffer中最后一个run-length,避免始终从头开始寻址。
举个栗子
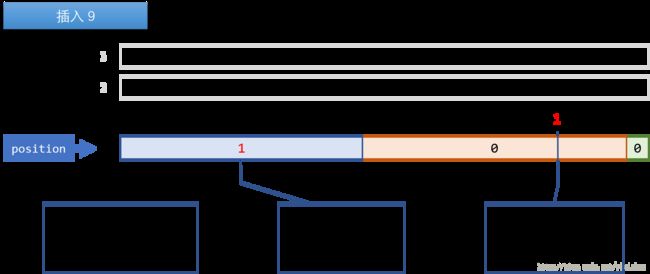
先插入9
因为要插入9,导致[0, 63]范围变成了Dirty Word,需要存储为字面量,因此会发生下面这些步骤:
- 将Buffer中第0个run-length的高位Number of Literal Words部分改为1,表示后面的一个
long为字面量; - 在Buffer中下标为1的位置插入一个表示字面量的
long,表示[0, 63]范围的值。因为插入了9,所以第9位的位置需要设为1(最低位为第0位)。
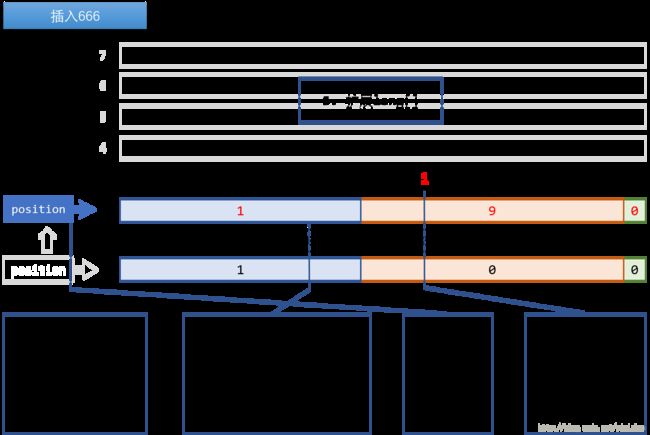
再插入666
再插入666的话,如果不压缩,那么将会形成这样的数组:
[640, 703]:Dirty Word,包含值666
[576, 639]:全0
[512, 575]:全0
[448, 511]:全0
[384, 447]:全0
[320, 383]:全0
[256, 319]:全0
[192, 255]:全0
[128, 191]:全0
[ 64, 127]:全0
[ 0, 63]:Dirty Word,包含值9可以看到,除了[0, 63]和[640, 703]两个Dirty Word,中间的9个long全都是0,是可以进行run-length压缩的。步骤如下:
- 在Buffer中下标为2的位置插入一个run-length,其中Running Bit为0(压缩的是0),Running Length为9(压缩了9×64位),Number of Literal Words为1(后面有一个Dirty Word);
- 将
position指向2,保持始终指向最后一个run-length; - 在Buffer中下标为3的位置插入一个字面量,表示
[640, 703],其中第26位为1,表示插入了值666。 - 目前Buffer已满,将数组大小由4扩展为8,以备后用。
run-length和字面量的转换
对于一个字面量
字面量代表的64位范围内既有0又有1,如果经过某些操作后,恰好所有0都变成了1,或者所有的1都变成了0,那么这个字面量就会被转换为run-length。
需要进行以下操作:
- 因为自己不再是字面量了,所以需要减少前一个run-length的Number of Literal Words的值。
- 检查前后相邻的
long是不是run-length,如果是的话能不能与自己合并。如果合并的话,合并后当前位置将会变成空位,需要将后面的数据整体前移。 - 如果转换后自己变成最后一个run-length,需要将position指向自己。
对于一个run-length
run-length代表了至少一个、多则成百上千个64位区间全都是相同的bit。如果某些操作导致其中出现一个异常值,将会切断当前run-length,插入至少一个字面量。
需要进行以下操作:
- 如果异常值出现在run-length的前64位或末尾64位,则需要收缩run-length的大小,在前面或后面插入一个字面量。
- 如果异常值出现在run-length的中间,则会将当前run-length切成两个较短的run-length,中间插入一个字面量。
- 如果当前run-length只包含64位,则直接将当前run-length替换为一个字面量。
- 上述操作完成后,更新发生变动的字面量前面的Number of Literal Words值。
总结
- 存储结构简单,只有一个大大的
long[],在bitmap较大时对GC不太友好。 - 除了有一个
position指向最后一个run-length,其他再没有能帮助随机访问的措施了,这就意味着,基本上所有的对bitmap的随机访问全都要从头开始过一遍,时间是线性的。不过,人家是完全的行程压缩,说随机访问有点欺负人,这种bitmap本身就不适合随机访问,大家也不要这样用。 - 总觉得压缩差那么点意思。。在极端情况下,压缩率甚至是负的。比如,你每隔64插入一个值试试。。
其实我不应该先研究RoaringBitmap再来研究EWAH的,现在看起来怎么都不如RoaringBitmap了。。
后面我会专门写一篇来比较RoaringBitmap和EWAHCompressedBitmap的性能指标,用数据来说话。