数据结构_堆_Java中的实现类

 

1.数据结构：堆（Heap）

https://www.jianshu.com/p/6b526aa481b1

 

2.Java实现最大堆

https://www.jianshu.com/p/257820688bf1

 

3.java借助PriorityQueue实现小根堆和大根堆

https://blog.csdn.net/zcf1784266476/article/details/68961473

 

我们先来了解下堆的基本概念：

 

基本概念

堆就是用数组实现的二叉树，所有它没有使用父指针或者子指针。堆根据“堆属性”来排序，“堆属性”决定了树中节点的位置。

堆的常用方法：

• 构建优先队列
• 支持堆排序
• 快速找出一个集合中的最小值（或者最大值）

堆属性

 

   堆分为两种：最大堆和最小堆，两者的差别在于节点的排序方式。

    在最大堆中，父节点的值比每一个子节点的值都要大。在最小堆中，父节点的值比每一个子节点的值都要小。这就是所谓的“堆属性”，并且这个属性对堆中的每一个节点都成立。

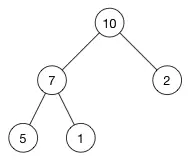
例子：

   这是一个最大堆，，因为每一个父节点的值都比其子节点要大。10 比 7 和 2 都大。7 比 5 和 1都大。

   根据这一属性，那么最大堆总是将其中的最大值存放在树的根节点。而对于最小堆，根节点中的元素总是树中的最小值。堆属性非常的有用，因为堆常常被当做优先队列使用，因为可以快速的访问到“最重要”的元素。

 

注意：

     堆的根节点中存放的是最大或者最小元素，但是其他节点的排序顺序是未知的。例如，在一个最大堆中，最大的那一个元素总是位于 index 0 的位置，但是最小的元素则未必是最后一个元素。唯一能够保证的是最小的元素是一个叶节点，但是不确定是哪一个。

 

 

Java中的实现

   借助Java 中的类 PriorityQueue 可以实现小根堆和大根堆。

/**
 * An unbounded priority {@linkplain Queue queue} based on a priority heap.
 * The elements of the priority queue are ordered according to their
 * {@linkplain Comparable natural ordering}, or by a {@link Comparator}
 * provided at queue construction time, depending on which constructor is
 * used.  A priority queue does not permit {@code null} elements.
 * A priority queue relying on natural ordering also does not permit
 * insertion of non-comparable objects (doing so may result in
 * {@code ClassCastException}).
 *
 * 
The head of this queue is the least element
 * with respect to the specified ordering.  If multiple elements are
 * tied for least value, the head is one of those elements -- ties are
 * broken arbitrarily.  The queue retrieval operations {@code poll},
 * {@code remove}, {@code peek}, and {@code element} access the
 * element at the head of the queue.
 *
 * 
A priority queue is unbounded, but has an internal
 * capacity governing the size of an array used to store the
 * elements on the queue.  It is always at least as large as the queue
 * size.  As elements are added to a priority queue, its capacity
 * grows automatically.  The details of the growth policy are not
 * specified.

通过上面介绍，可以看到第一个元素，就是这个排序的最后一个元素。

 

 

下面我们看下PriorityQueue 的具体使用：

package leetcode;

import java.util.Comparator;
import java.util.PriorityQueue;

/**
 * Created by szh on 2020/6/21.
 * @author szh
 */
public class HeapTest {


    public static void main(String[] args){

        PriorityQueue minPriorityQueue = new PriorityQueue<>(10, new Comparator() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return o1.compareTo(o2);
            }
        });


        int[] result_1 = new int[]{1, 2, 4, 3, 2, 2, 2, 2, 2};

        for(int tmp : result_1){
            minPriorityQueue.offer(tmp);
        }

        while(minPriorityQueue.size()>0){
            System.out.println(minPriorityQueue.poll());
        }


        System.out.println("-------------------------------");
        System.out.println("-------------------------------");
        System.out.println("-------------------------------");



        PriorityQueue maxPriorityQueue = new PriorityQueue<>(10, new Comparator() {
            @Override
            public int compare(Integer o1, Integer o2) {
                return -o1.compareTo(o2);
            }
        });

        int[] result_2 = new int[]{1, 2, 4, 3, 2, 2, 2, 2, 2};

        for(int tmp : result_2){
            maxPriorityQueue.offer(tmp);
        }

        while(maxPriorityQueue.size()>0){
            System.out.println(maxPriorityQueue.poll());
        }


        System.out.println("-------------------------------");
        System.out.println("-------------------------------");
        System.out.println("-------------------------------");

    }


}

输出：

1
2
2
2
2
2
2
3
4
-------------------------------
-------------------------------
-------------------------------
4
3
2
2
2
2
2
2
1
-------------------------------
-------------------------------
-------------------------------