leetcode刷题总结之回溯法
前言:
最近太懒了,好久都没写总结了。回溯法是看labuladong的详解回溯法入的门,然后看了《计算机算法设计与分析》第5章的回溯法部分弄清了原理,在leetcode上做了差不多20个题,今日总结一下,供以后复习用。
回溯法的定义:
回溯法有通用解法的美称,对于很多问题,如迷宫等都有很好的效果。回溯法实际就是对问题的解空间树采用深度优先搜索的方式,搜索需要解决问题的任一解或者所有解,它是一个既带系统性又带跳跃性的搜索算法。
回溯法的解空间树:
所有可行解构成的多叉树成为解空间树,解空间树中从根节点到叶子节点的一条路径为回溯法的任一解。对于n=3时,0/1背包表示的解空间树,如下:
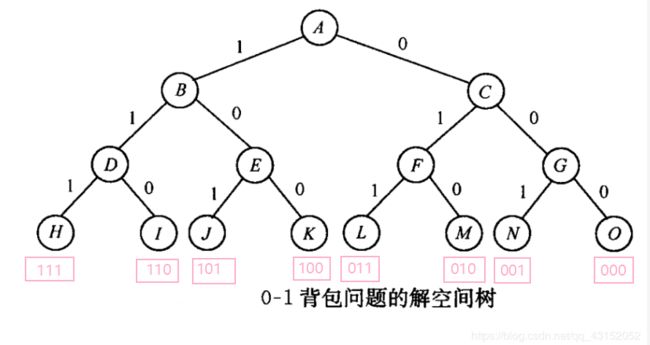
回溯法的解题步骤:
- 1)针对所给问题,定义问题的
解空间(一个可行解) - 2)确定易于搜索的
解空间结构(选择列表) - 3)以
深度优先搜索的方式搜索解空间,并在搜索过程中用剪枝函数避免无效搜索
注:剪枝函数分为约束函数和限界函数。约束函数表示在解空间树的扩展节点处剪去不满足约束的子树,限界函数表示减去得不到最优解的子树。
回溯法的框架:
//choicelist:表示可以进行选择的列表,相当于树中可选用左节点还是右节点
//track:表示为决策路径,相当于在解空间树中为根节点到某个叶子节点的路径
//result:表示存放根节点到所有叶子节点的所有路径,所有可行解
backtrack(choicelist,track,result)
{
if(track is ok)result.push(track);//找到一个可行解
else{
for choice in choicelist:
//choose过程:选择一个choice加入track,相当于在树中选择一个节点加入路径
track.push(choice);
//进入下一步决策
backtrack(choicelist-choice,track,result);
//unchoose过程:从track中撤销上面的选择,相当于在树中移除上一次选择的节点
track.insert(choice);
}
}
回溯法的时间复杂度:
- 对于像0/1背包这种问题,每次要做的决策是
选或不选,相应的解空间树为子集二叉树,共2^(n+1)-1==叶子节点,所以时间复杂度为O(2^n)。 - 对于像全排列这种问题,每次要做的决策是还剩下的列表选一个数字,相应的解空间树为
排列树,共n!个叶子节点,所以时间复杂度为O(n!)。 - 注:无论是子集树还是排列树,不过就是
可选择的列表不一样罢了。
习题解析:
10.正则表达式匹配:回溯框架变形,细节问题比较难想,具体可看题解。
17.电话号码的字母组合:回溯法的标准框架,没啥变化,具体可看题解。
22.括号生成:本题使用n来表示左括号可以使用个数,用index来表示右括号可以使用的次数。在每使用掉一个左括号时,对应可以使用右括号的数量+1,因为这样可以保证左右括号是对等的(也就是先有左括号,然后再有右括号,这样就避免无效括号了)。
37.解数独:回溯框架+剪枝,其他细节问题较多,具体可看题解。
39.组合总和:回溯的标准框架,细节问题可看题解。
40.组合总数 Ⅱ:在39.组合总和的基础上加上剪枝即可。
44.通配符匹配:回溯框架变形,细节问题可看题解。
46.全排列:回溯的标准框架,细节问题可看题解。
47.全排列 Ⅱ:在46.全排列的基础上加上剪枝,针对同一层次的计算,对连续的相同的元素只选取一个进行后续的替换,即可等价于基础全排列。
51.N皇后:回溯框架+剪枝(判断皇后是否为可行皇后),细节问题可看题解。
52.N皇后 Ⅱ:本题在51.N皇后基础上直接返回所有可行皇后的个数。
60.第k个排列:本题使用回溯超时了,遂使用数学方法康托展开法来解题。
77.组合:本题与全排列的区别在于全排列中会出现[1,2]、[2,1]这样的排列,然而在组合中是不能存在的,所以我们每次需要将组合数第一个数固定,然后组合数之后的数依次增大。
78.子集:与77.组合的算法思想一样,发现共性便可求解。
79.单词搜索:本题又是一道回溯法经典练习题,212.单词搜索 Ⅱ是使用前缀树+回溯法解决的,而本题难度相对而言小一点,直接使用回溯法就好了。
89.格雷编码:这里用暴力法比回溯法简单一点,不过两份代码都提供了,具体可看题解。
93.复原IP地址:回溯法,ip地址有三个点,分为四段,每段的数字范围必须在[0,255]内,注意0只能作为单独一个段,比如:0.0.0.124,细节问题具体可看题解。
131.分割回文串:思想与N皇后的回溯法差不多的模板,寻找到所有的可行解后,回溯完成!
282.给表达式添加运算符:本题最难最难的就是处理乘法了,由于乘法的优先级比加、减法高,所以在遇到乘号时需要回退到上一步,然后将上一步的操作数与乘法进行运算。