机器学习——学习笔记（一）

初次接触机器学习这一陌生的学科，特地将我的学习笔记和有关资料整理在博客中。

机器学习概念

 

机器学习(Machine Learning, ML)是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域，它主要使用归纳、综合而不是演绎。-------百度百科

机器学习有下面几种定义： “机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能”。 “机器学习是对能通过经验自动改进的计算机算法的研究”。 “机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。” 一种经常引用的英文定义是：A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

可以看出这是一门非常复杂的学科，涉及到很广的知识面。

 机器学习的类型

机器学习分为：监督学习，无监督学习，半监督学习（强化学习）等。

监督学习：把训练数据（有特征和标签）丢给机器，机器从给定的训练数据集中学习出一个函数（模型参数），当新的数据（只有特征没有标签）到来时，可以根据这个函数判断出结果（标签）。

无监督学习：只给计算机训练数据，不给结果（标签），因此计算机无法准确地知道哪些数据具有哪些标签，只能凭借强大的计算能力分析数据的特征，从而得到一定的成果，通常是得到一些集合，集合内的数据在某些特征上相同或相似。

半监督学习：其训练数据的一部分有标签，另一部分没有标签，让机器不依赖外界交互、自动地利用未标记样本来提升学习性能。

泛化能力

泛化能力（generalization ability）是指机器学习算法对新鲜样本的适应能力。  学习的目的是学到隐含在数据背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，该能力称为泛化能力。-----百度百科

通俗来讲就是指学习到的模型对未知数据的预测能力。 

在机器学习领域中，当我们讨论一个机器学习模型学习和泛化的好坏时，我们通常使用术语：过拟合和欠拟合.

过拟合和欠拟合是机器学习算法表现差的两大原因。

过拟合和欠拟合

过拟合：指的是referstoa模型对于训练数据拟合程度过当的情况。当某个模型过度的学习训练数据中的细节和噪音，以至于模型在新的数据上表现很差，我们称过拟合发生了。这意味着训练数据中的噪音或者随机波动也被当做概念被模型学习了。而问题就在于这些概念不适用于新的数据，从而导致模型泛化性能的变差。

欠拟合：指的是模型没有很好的抓住数据的特征，没有很好的对数据拟合，导致预测结果也不好。

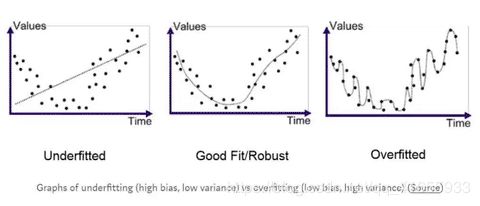
上图中从左到右依次为欠拟合，拟合，过拟合。

可以看出，过拟合是对数据过分关注，而欠拟合是对数据的忽视，从而都达不到较好的拟合。

解决方法：使用验证集对模型进行校正可以避免实际过程中造成的欠拟合和过度拟合

模型中的方差和偏差

在数据科学学科中， 过度拟合（overfit）模型被解释为一个从训练集（training set）中得到了高方差（variance）和低偏差（bias），导致其在测试数据中得到低泛化（generalization）的模型。而欠拟合是一个低方差、高偏差的模型。但是，模型中的方差和偏差又是什么呢？

方差可以理解为为了响应训练集时模型所产生的变化。若我们只是单纯的去记忆训练集，我们的模型将具有高方差：它高度取决于训练集数据。当这样一个具有高方差的模型应用到一个新的测试集上时，这个模型将无法获得很好的表现。因为在没有训练集数据的情况下模型将迷失方向。就好比一个学生只是单纯复习了教科书上列出的问题，但这却无法帮助他解决一些实际的问题。

偏差（bias），作为与方差相对的一个概念，表示了我们基于数据所做出的假设的强度（有效性）。低偏差看似是一个正向的东西，因为我们可能会有这样的想法：我们并不需要去带着倾向性思维看待我们的数据。然而我们却需要对数据表达的完整性持怀疑态度。因为任何自然处理流程都会生成噪点，并且我们无法自信地保证我们的训练数据涵盖了所有这些噪点。所以我们在开始学习英语之前需要明白，我们无法通过死记硬背莎士比亚的名著来熟练掌握英语。

总体来说，偏差关系到数据被忽略的程度，而方差则关系到模型和数据的依赖程度。在所有的建模过程中，偏差和方差之间永远存在着一个权衡问题，并且需要我们针对实际情况找到一个最佳的平衡点。

交叉验证

交叉验证是在机器学习建立模型和验证模型参数时常用的办法。交叉验证，顾名思义，就是重复的使用数据，把得到的样本数据进行切分，组合为不同的训练集和测试集，用训练集来训练模型，用测试集来评估模型预测的好坏。在此基础上可以得到多组不同的训练集和测试集，某次训练集中的某样本在下次可能成为测试集中的样本，即所谓“交叉”。　

简单交叉验证，所谓的简单，是和其他交叉验证方法相对而言的。首先，我们随机的将样本数据分为两部分（比如： 70%的训练集，30%的测试集），然后用训练集来训练模型，在测试集上验证模型及参数。接着，我们再把样本打乱，重新选择训练集和测试集，继续训练数据和检验模型。最后我们选择损失函数评估最优的模型和参数。　

S折交叉验证（S-Folder Cross Validation）。和第一种方法不同，S折交叉验证会把样本数据随机的分成S份，每次随机的选择S-1份作为训练集，剩下的1份做测试集。当这一轮完成后，重新随机选择S-1份来训练数据。若干轮（小于S）之后，选择损失函数评估最优的模型和参数。

留一交叉验证（Leave-one-out Cross Validation），它是第二种情况的特例，此时S等于样本数N，这样对于N个样本，每次选择N-1个样本来训练数据，留一个样本来验证模型预测的好坏。此方法主要用于样本量非常少的情况，比如对于普通适中问题，N小于50时，我一般采用留一交叉验证。

通过反复的交叉验证，用损失函数来度量得到的模型的好坏，最终我们可以得到一个较好的模型。那这三种情况，到底我们应该选择哪一种方法呢？一句话总结，如果我们只是对数据做一个初步的模型建立，不是要做深入分析的话，简单交叉验证就可以了。否则就用S折交叉验证。在样本量少的时候，使用S折交叉验证的特例留一交叉验证。

 

 

 

参考资料：https://www.cnblogs.com/pinard/p/5992719.html

                  http://www.28robot.com/jishu/jqxx/7545.html