Tensorflow2.0的学习之路之 --numpy科学计算库-超详细
文章目录
- tensorflow2.0学习记录
- 多维数组
- 创建Numpy数组
- 创建数组
- 数组的属性
- 创建特殊的数组
- 数组运算
- 数组间的运算
- 数组元素间的运算
- 数组的堆叠
- 矩阵和随机数
- 矩阵的运算
- 随机数
- 感谢观看
tensorflow2.0学习记录
序言:这一篇我们主要讲一下numpy库
多维数组
纸上的一个点、一条线是一维空间的物体,由无数条线组合成的一张理想的不计厚度的纸属于二维空间的物体,我们人类所处的世界是三维空间…
在python中,我们可以用数组来对不同维度的事物进行描述。
通常在机器学习中,我们需要把所有的输入数据都转变为多维数组的形式,
以成绩表格为例: 上图中左边两个数组都属于一维数组
上图中左边两个数组都属于一维数组
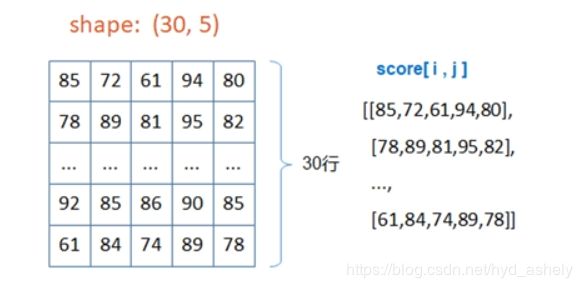
最右侧的数组则是二维数组的形式,包含以行(学生)、列(课程)组成的信息阵,得知行列之后即可知晓对应的学生的某门课成绩。
要想取得成绩,我们用score[ i, j ],具体理解为表格中第i+1行,第j+1列的数据(python中以0为第一)
一维数组书写方式:
score = [ 85, 72, 61, 92, 80, ]
二维数组的书写方式:
score = [ [ 85, 72, 61, 92, 80, ], [ 78, 89, 81, 95, 82, ], ...[ 92, ...85, ], [ 61, 84, 74, 89, 78, ] ]
二维数组书写方式(美化版):
socre = [ [ 85, 72, 61, 92, 80, ],
[ 78, 89, 81, 95, 82, ],
[ ... ]
[ 61, 84, 74, 89, 78, ] ]
数组的形状:描述数组的维度,以及各个维度内部的元素个数。
描述:形如( n0,n1,…nm ),用一个元组来表示,有几个数字就有几个维度,每个数字对应这个维度的长度。
以上述示例的一维数组为例,其形状为:shape:( 5, )

以上述示例中的二维数组为例,其形状为:shape( 30, 5 )
那么三维数组:
假设有10个班,每个班有30名学生,每名学生对应5个科目的成绩

四维数组:
在三维数组表示10个班级的信息基础之下,以10个班级为一个年级,统计4个年级的数据,可以形成一个数据库。

创建Numpy数组
Numpy简介:
全名:Numeric Python
1.提供多维数组。矩阵的常用操作和一些搞笑的科学计算函数。
2.底层运算是用过C语言实现的,树立速度快。效率高,越是大规模的数据处理优化越明显。
3.可以直接完成数组和矩阵的运算,无需循环
导入Numpy库
要想使用numpy库,就需要导入,有两种方法:
import numpy as np(推荐)
在后面使用numpy数组的时候需要加上前缀 np
from numpy import*
这种导入方法不需要加前缀,但是很可能与python同名函数发生混淆。
创建数组
使用函数array( [列表] / (元组) ):
>>>a = np.array( [ 0, 1, 2, 3, ] )
#直接输入a可以看到数组的定义
>>>a
array( [ 0, 1, 2, 3, ] )
#使用print输出a可以看到数组中的元素
>>>print(a)
[ 0, 1, 2, 3, ]
#使用type可以看到数组的类型,在numpy中,数组是一个ndarray对象
>>>type(a)
< calss 'numpy.ndarray' >
除此之外,我们还可以用索引来访问数组中的某一元素,也可以对数组进行切片。
数组的属性
| 属性 | 描述 |
|---|---|
| ndim | 数组的维度 |
| shape | 数组的形状 |
| size | 数组元素的总个数 |
| dtype | 数组中元素的数据类型 |
| itemsize | 数组中每个元素的字节数 |
利用我们上一部分创建的数组进行使用举例:
>>>a.shape
( 4, )
>>>a.ndim
1
>>>a.size
4
numpy中要求数组中所有元素的数据类型必须是一致的
numpy中又包含了许多python中没有的数据类型:
- int8、uint8、int16、uint16、int32、uint32、int64、uint64
- float16、float32、float64、float128
- complex64、complex128、complex256
- bool、object、string_、unicode_
数组元素的数据类型
在创建数组时,我们可以用dtype规定数据类型:
array( [列表]/(元组), dtype=数据类型 )
例如:
a = np.array( [ 0, 1, 2, 3 ], dtype = np.int64 )
#这里np.int64可以是int64或者'int64',表达意思一样
>>>a
array( [ 0, 1, 2, 3 ], dtype = np.int64 )
已知一个数组,需要我们知晓他的数据类型:
>>>a.dtype
dtype( 'int64' )
在使用python列表或元组、创建numpy数组时,所创建的数组类型由原来的元素类型推导而来
创建特殊的数组
numpy中提供了相应的函数来创建特殊的数组
| 函数 | 功能描述 |
|---|---|
| np.arange() | 创建数字序列数组 |
| np.ones() | 创建全1数组 |
| np.zeros() | 创建全0数组 |
| np.eye() | 创建单位矩阵 |
| np.linspace | 创建等差数列 |
| np.logspace() | 创建等比数列 |
- arange()函数:创建一个由数字序列构成的数组
与python中的range()函数相似,产生一个数字序列,从起始数字开始,以结束数字结尾不包含结束数字。
而这里的arange()函数则包含更多的参数:
np.arange( 起始数字,结束数字,步长,dtype=数据类型 )
要点:
- 前闭后开:数字序列中吧不傲阔结束数字
- 起始数字省略时默认从0开始
- 步长省略时。默认为1
示例:
a = np.arange(0,5,0.7)
print( a )
#得到
>>[0. 0.7 1.4 2.1 2.8 3.5 4.2 4.9]
ones()函数:创建一个元素全部为1的数组
np.ones( shape, dtype=数据类型 )
示例:
print(np.ones( (5,5), ))
#dtype可以省略,得到结果
>>[[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1.]]
zeors()函数:创建一个元素全为0的数组
np.zeros( shape, dtype=数据类型 )
示例:
print(np.zeros( (5,5), ))
#dtype可以省略,得到结果
>>[[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0.]]
eye()函数:创建一个单位矩阵
np.eye( shape )
示例:
print(np.eye(5))
>>[[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
[0. 0. 1. 0. 0.]
[0. 0. 0. 1. 0.]
[0. 0. 0. 0. 1.]]
linspace()函数:创建等差数列
np.linspace( start, stop, num=? )
其中,start是起始数字,stop是终止数字,最后的结果包含终止数字,num是数列中的元素个数。
示例:
print(np.linspace( 3,21,7 ))
>>[ 3. 6. 9. 12. 15. 18. 21.]
logspace()函数:创建一个等比数列
np.logspace( start, stop, num=?, base=? )
其中,形如数学中 qn, start是起始幂次,stop是终止幂次,最后的结果包含终止幂次,num是数列中的元素个数,base是底数,即q.
示例:
print(np.logspace( 1, 5, 5, base= 2 ))
>>[ 2. 4. 8. 16. 32.]
asarray()函数:将列表或元组转化为数组对象
功能上大致与arrya()函数一样,但区别是:
如果数据源本身就是一个数组对象时,array()会复制出一个新的副本,占用新的内存,但asarray()不会
数组运算
数组元素的切片:前面讲到可以对数组进行切片,这里以三维数组为例,一维二维都是同样的道理。
示例:
#创建一个三维数组
happy = np.array( [ [ [0, 1, 2, 3, ],
[4, 5, 6, 7, ],
[8, 9, 10, 11, ] ] ,
[ [12, 13, 14, 15,],
[16, 17, 18, 19,],
[20, 21, 22, 23,] ] ] )
#对三维数组进行切片
print( happy[:,:,0 ] )
>>[[ 0 4 8]
[12 16 20]]
print( happy[1,0,:] )
>>[12 13 14 15]
改变数组的形状
如果我们想要在已有的数组上做一些改变,让它依旧保持元素个数不变,改变数组形状,可以考虑使用以下两个函数:
| 函数 | 功能描述 |
|---|---|
| np.reshape(shape) | 不改变当前数组,按照shape创建新的数组 |
| np.resize(shape) | 直接改变当前数组,按照shape创建数组 |
示例:
#创建一个1维数组
happy = np.array( [ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ] )
#分别使用两种函数,呈现对比
print( happy.reshape( 4,3 ) )
print( happy )
print( happy.resize( 4,3 ) )
print( happy )
#得到结果:
>>[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
>>[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ]
>>[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
>>[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
当我们改变数组形状是,应该考虑到数组中的元素的个数,确保改变前后,元素总个数相等
特别的,当时用 reshape() 函数时,可以在括号内填写-1来代表某一维度的元素个数取值,这一取值通常根据整个数组中的元素个数、以及其他维度的取值,来自动计算出政委杜的取值。
示例:
#仍然利用上面举得happy数组的例子
print( happy.reshape( -1,1 ) ) #得到一个12*1的二维矩阵
>>[[ 0]
[ 1]
[ 2]
[ 3]
[ 4]
[ 5]
[ 6]
[ 7]
[ 8]
[ 9]
[10]
[11]]
print( reshape( -1 ) ) #形成一个具有十二个元素的一维数组,当然,和原来的happy数组一样
>>[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, ]
数组间的运算
数组也遵从四则运算法则。
- 一维数组与多维数组相加,相加时,会将一维数组扩展至多维数组,即:一维数组与多维数组的相同维度的元素依次相加。
示例:
a = np.array( [ 0, 1, 2, 3 ] )
b = np.array( [ [ 0, 1, 2, 3, ], [ 4, 5, 6, 7, ] ] )
print( a + b )
>>[ [ 0, 2, 4, 6 ],
[ 4, 6, 8, 10 ] ]
- 数组的相加,需要保证相加的数组形状和长度一致,否则会出错
示例:
a = np.array( [ 0, 1, 2, 3 ] )
b = np.array( [ 2, 3, 4, 5 ] )
print( a+b )
>>[ 2, 4, 6, 8 ]
- 数组间的减法、乘法、除法运算,和加法运算规则相同
- 当两个数组中的元素数据类型不同时,精度低的数据类型会自动转化为净度高的数据类型,然后再进行运算。
特别注意,二维数组实际上就是矩阵,矩阵的应用非常广泛。
我们在使用二维数组的乘法时,或许会期望它通过矩阵的乘法法则得到结果,于是:

幂运算:对数组中的每个元素求n次方
示例:
happy = np.arange(12).reshape(3,4) #这里直接创建数组之后改变了它的形状
print( happy**2)
>>( [ [ 0, 1, 4, 9 ],
[ 16, 25, 36, 49 ],
[ 64, 81, 100, 121 ] ] )
矩阵运算:转置与求逆
- 矩阵转置: np.transpose()
- 矩阵求逆:np.linalg.inv()
数组元素间的运算
numpy对数组间的元素提供了这些函数进行运算:
| 函数 | 功能描述 |
|---|---|
| numpy.sum() | 计算所有元素的和 |
| numpy.prod() | 计算所有元素的乘积 |
| numpy.diff() | 计算数组的相邻元素之间的差 |
| np.sqrt() | 计算各元素的平方根 |
| np.exp() | 计算各元素的指数值 |
| np.abs() | 取各元素的绝对值 |
以np.sum()函数为例:
首先我们要清楚在数组中轴和秩的概念
轴:数组中的每一个维度被称为一个轴
秩:轴的个数
对于多维数组中的轴,每个轴都有它的索引。
 从图中很清晰的看到,一维数组只有一个轴,它的索引是0,以此类推
从图中很清晰的看到,一维数组只有一个轴,它的索引是0,以此类推
因此,不仅仅我们可以求出整个数组的元素之和,我们也可以通过轴的索引求出某一个维度的元素相加之和。

数组的堆叠
有时候我们希望把两个数组堆叠成为维度更高的数组,这就需要我们用到**np.stack()**函数
形如:np.stack( (数组1,数组2,…), axis )
示例:
happy = np.array( [ 1, 2, 3 ] )
sad = np.array( [ 4, 5, 6 ] ) #创建两个数组
np.stack( ( happy,sad ), axis = 0 ) #在轴=0上进行堆叠
>>[ [ 1, 2, 3 ],
[ 4, 5, 6 ] ]
np.stack( ( happy,sad ), axis = 1 ) #在轴1上进行堆叠
>>[ [ 1, 4 ],
[ 2, 5 ],
[ 3, 6 ] ]
矩阵和随机数
在numpy库中,除了数组对象,还提供了矩阵对象
matrix(字符串/列表/元组/数组)
mat(字符串/列表/元组/数组)(简写版)
示例:
>>>a= np.matrix( '1 2 3; 4 5 6' )
>>>a
matrix( [[1,2,3],
[4,5,6]] )
和numpy数组一样,我们也可以求矩阵的属性
| 属性 | 说明 |
|---|---|
| .ndim | 矩阵的维度 |
| .shape | $矩阵的形状 |
| .size | 矩阵的元素个数 |
| .dtype | 元素的数据类型 |
矩阵的运算
矩阵相乘:a*b
矩阵转置:.T(大写)
矩阵求逆:.I(大写)
随机数
对于均匀分布的数组:
- low: 采样下界,float类型,默认值为0
- high: 采样上界,float类型,默认值为1;
- size: 输出样本数目,为int或元组(tuple)类型,例如,size=(m,n,k), 则输出mnk个样本,缺省时输出1个值。
对于正态分布的数:
4. 参数loc(float):正态分布的均值,对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布
5. 参数scale(float):正态分布的标准差,对应分布的宽度,scale越大,正态分布的曲线越矮胖,scale越小,曲线越高瘦。
6. 数size(int 或者整数元组):输出的值赋在shape里,默认为None。
需要知道的是,这些随机数并不是真正意义上的随机数,以下几个概念帮助我们更好地理解随机数的产生
- 伪随机数:由随机种子,根据一定的算法生成的
- 随机种子:制定随机数生成时所用算法开始的整数值
– 如果使用相同的seed()值,则每次生成的随机数都相同。
– 如果不设置这个值,则根据时间来自己选择这个值,此时每次生成的随机数因时间差异而不同。
– 采用seed()函数设置随机种子,仅一次有效
– 随机数产生的算法,和系统有关,即使随机种子一样,windows和linux产生的随机数可能不一样
打乱顺序函数:np.random.shuffle(序列)
如果要打乱多维数组,那么只会打乱第一维度的元素
示例:
>>>happy = np.array( [ [0, 1, 2, 3 ],
[4, 5, 6, 7 ],
[8, 9, 10, 11 ] ] )
>>>nnp.random.shuffle(happy)
[ [ 4,5,6,7 ],
[ 0,1,2,3 ],
[ 8,9,10,11 ] ]
感谢观看
文章部分图源:中国大学mooc-西安电子科技大学<神经网络与深度学习–Tensorflow2.0实战>
感谢观看,欢迎批评指正

