DataStructure_第八章 查找 ( 线性表查找 / 树形查找 / 散列查找 )

一/ 线性表查找

1》顺序查找

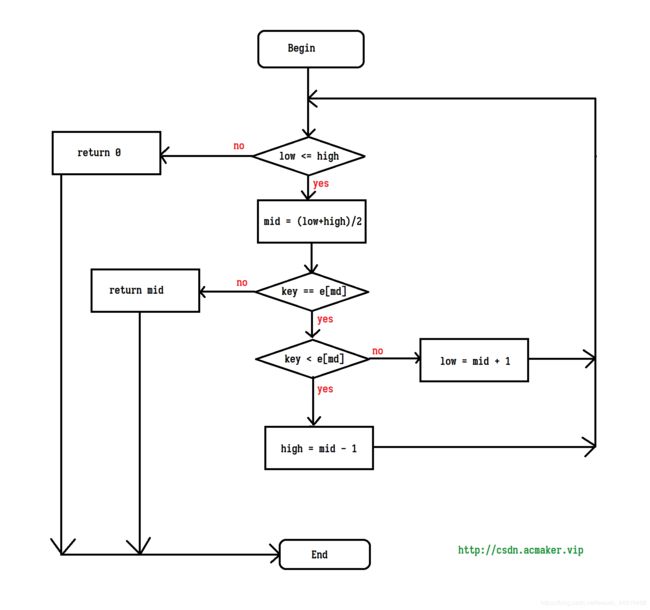
2》折半查找

// 默认低位为0
ll binarySearch(ElemType k) {
    for (ll l = 0, h = index, md; l <= h;) {
        md = (l + h) / 2;
        if (k == e[md])
            return md;
        else if (k < e[md])
            h = md - 1;
        else
            l = md + 1;
    }
    return 0;
}

3》分块查找

二/ 树形查找

1》二叉搜索树

概念

二叉搜索树又被称为二叉排序树，那么它本身也是一棵二叉树，那么满足以下性质的二叉树就是二叉搜索树，如图：

若左子树不为空，则 左 子树上所有节点的值都 == 小于 == 根节点的值；
若右子树不为空，则 右 子树上所有节点的值都 == 大于 == 根节点的值；
它的左右子树也要分别是二叉搜索树。

插入节点

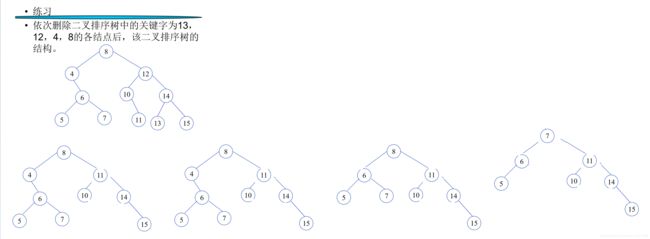
删除节点

若删除节点，
无子节点，则直接删除；
有一个子节点，则删除后上移；
有两个子节点，则删除后，将左边最大或右边最小节点上移；

2》平衡二叉树

概念

平衡二叉树要么是空树，要么做右子树高度叉绝对值小于等于1，并且左右子树也都是平衡二叉树。

所谓的左旋和右旋都是以子树为原点的：如b是a的子树，那么旋转就围绕b来进行。
如果b是a的左子树，那么就围绕b将a向右旋转，看着就像是a直接掉下来了，掉成了b的右子树。
如果b是a的右子树，那么就围绕b将a向左旋转，看着就像是a直接掉下来了，掉成了b的左子树。

调整

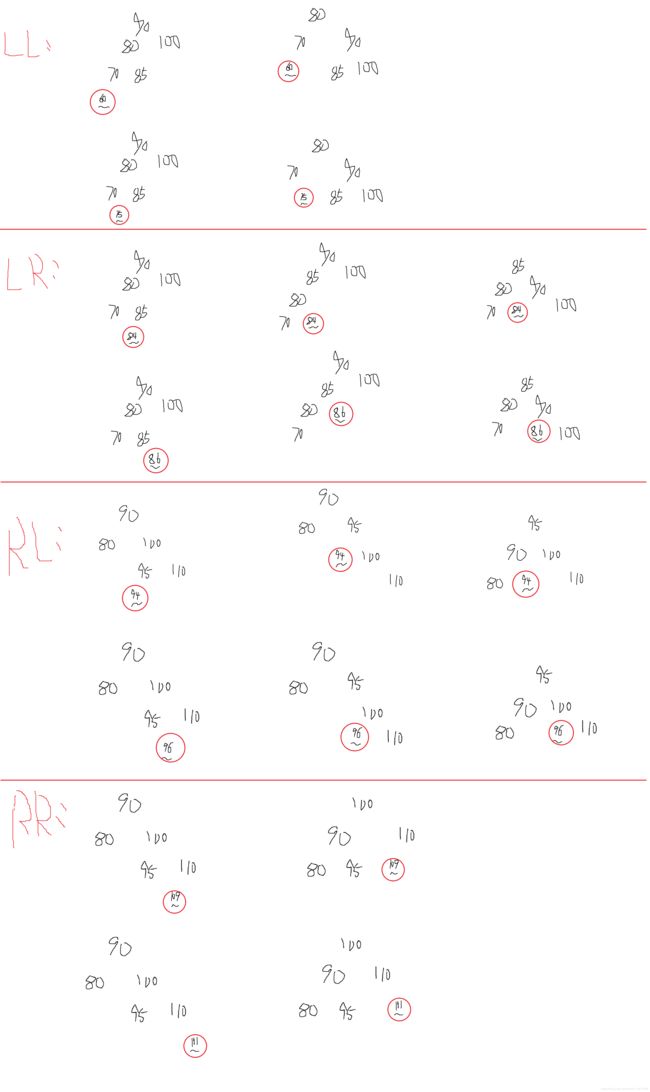
LL

以不平衡子树根节点子为中心，右旋转一下

LR

以插入节点的父节点为中心，先左旋一下，再右旋一下（注意，调整的范围只是子树的范围）

RL

以插入节点的父节点为中心，先右旋一下，再左旋一下（注意，调整的范围只是子树的范围）

RR

以不平衡子树根节点为中心，左旋转一下

枚举所有情况

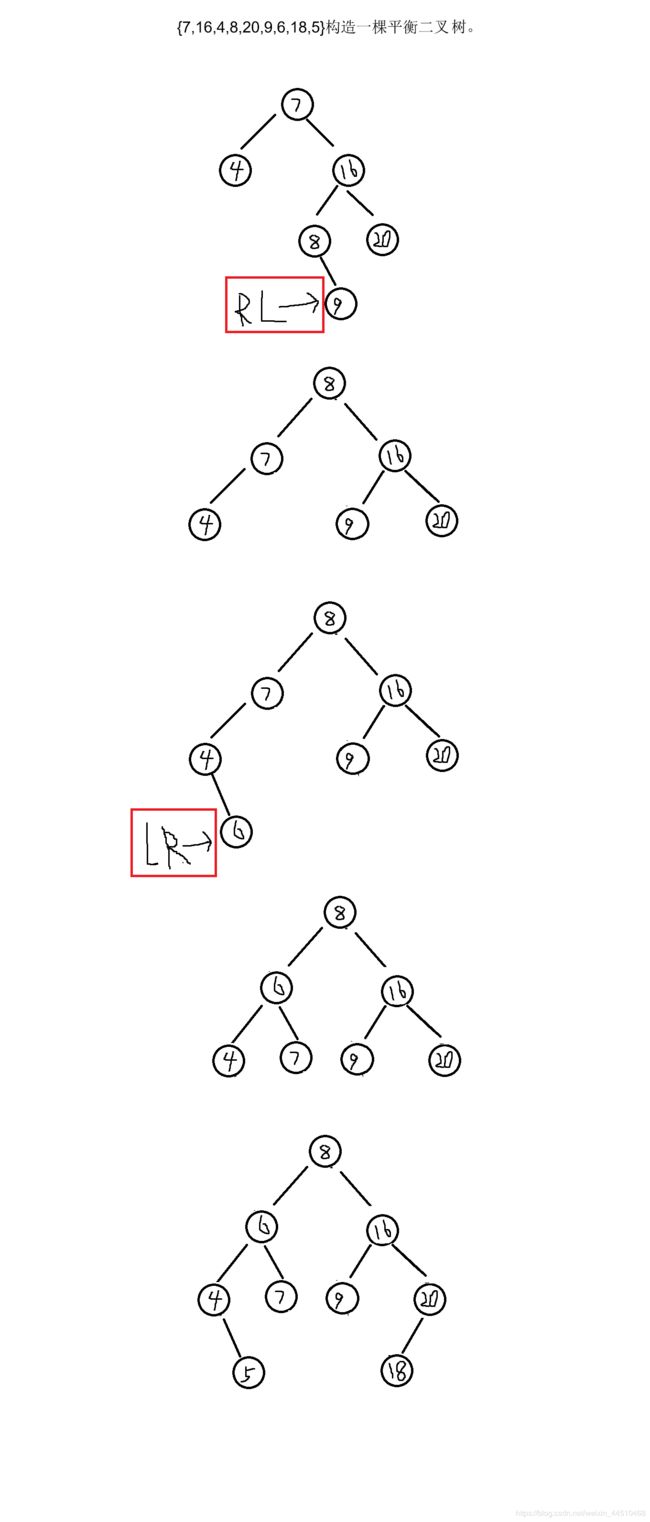
小例

感谢以下博客巧妙的idea！

https://www.cnblogs.com/cherryljr/p/6669489.html

https://www.cnblogs.com/huangxincheng/archive/2012/07/22/2603956.html

三/ 散列查找（哈希 ）

1、构造

数字分析法

平方取中法

分段叠加法

除留余数法

伪随机数法

2、冲突处理

1》开放探测法

h_i ( key ）= ( H(key)+d_i ) % TableSize;

线性探测再散列处理

d_i = 1，2，3，4，5，6，…，∞

二次探测再散列处理

d_i = 1，2，3，4，5，6，…，k², -k² （　k <= mod/2 )

---

小例：

已知哈希表空间 0~14

39 23 41 38 44 15 68 12 06 51

H( key ) = key % 13

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14
39		41	15	68	44	06				23	51	38	12

这里只写下冲突时候的处理

H(15) = 15%13 = 2
H₁(15) = H(15) + d₁ = (2+ 1²)%15 = 3

H(68) = 68%13 = 3
H₁(68) = H(68) + d₁ = (3+ 1²)%15 = 4

H(12) = 12%13 = 12
H₁(12) = H(12) + d₁ = (12 + 1²)%15 = 13

H(51) = 51%13 = 12
H₁(51) = H(51) + d₁ = (12 + 1² )%15 =13
H₂(51) = h₁(51) + d₂ = (12 - 1²) %15 = 11

伪随机探测再散列

2》再哈希法

3》链地址法

4》建立公共溢出区

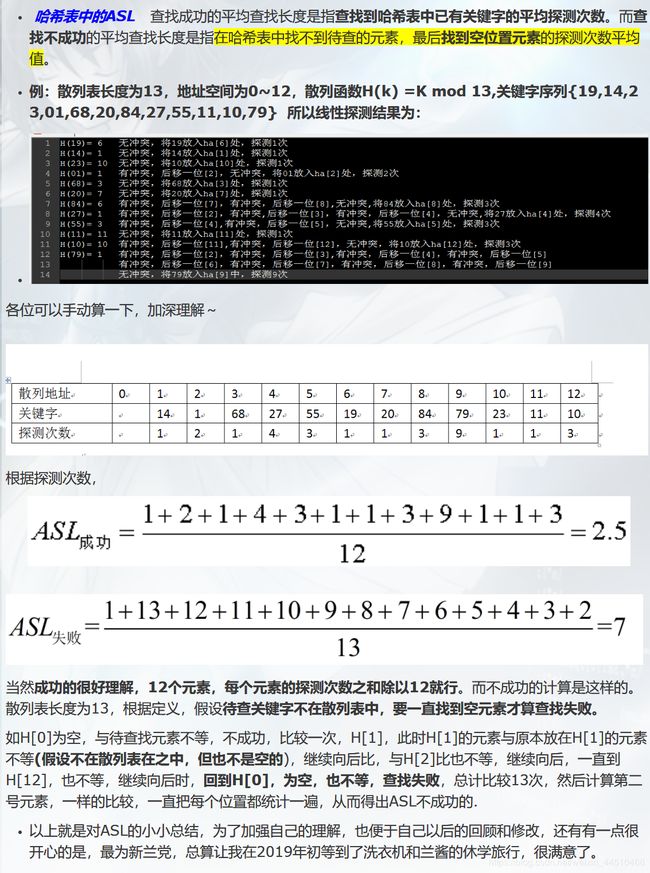
3、查找

计算平均查找长度

附一片讲的很易懂的关于三种查找方式ASL计算的博客

四/ 章末习题精选

折半查找的实现

由于题意是要求从失败返回0，成功范围下标，所以为了避免冲突数组只能从1开始存储

/***
 * @Author      : acmaker
 * @Date        : 2020-06-08 12:49:07
 * @LastEditTime: 2020-06-08 13:00:56
 * @FilePath    : \myCPlusPlusCode\DataStructure\Search\mooc.cpp
 * @Website     : https://csdn.acmaker.vip
 * @Description :
 */

#include 
using namespace std;
#define sc scanf
#define pf printf
typedef long long ll;

typedef ll ElemType;
const int MAX_SIZE = 1e3 + 1;
class ArrayList {
private:
    ElemType e[MAX_SIZE];
    ll index;
public:
    ArrayList();
    ll size();
    void add(ElemType data);
    ElemType get(ll i);
    ll binarySearch(ElemType k);
};
ArrayList::ArrayList() {
    index = 1;
}
ll ArrayList::size() {
    return index;
}
void ArrayList::add(ElemType data) {
    e[index++] = data;
}
ElemType ArrayList::get(ll i) {
    return e[i];
}
ll ArrayList::binarySearch(ElemType k) {
    for (ll l = 1, h = index, md; l <= h;) {
        md = (l + h) / 2;
        if (k == e[md])
            return md;
        else if (k < e[md])
            h = md - 1;
        else
            l = md + 1;
    }
    return 0;
}

int main(void) {
    ArrayList list;

    for (int i = 1; i < 11; ++i) {
        list.add(i);
    }

    for (int i = 1; i < 21; ++i) {
        cout << list.binarySearch(i) << endl;
    }

    return 0;
}

这个小例子是统计查找次数，其中顺序查找用了监视哨这个小技巧。那这里也贴上吧。

/***
 * @Author      : acmaker
 * @Date        : 2020-06-08 21:30:08
 * @LastEditTime: 2020-06-08 21:45:51
 * @FilePath    : \myCPlusPlusCode\DataStructure\ExperimentReport\FIVE\test.cpp
 * @Website     : http://csdn.acmaker.vip
 * @Description :
 */

#include 
using namespace std;
#define sc scanf
#define pf printf
typedef long long ll;

typedef ll ElemType;
const int MAX_SIZE = 1e3 + 1;
class ArrayList {
private:
    ElemType e[MAX_SIZE];
    ll index;
public:
    int cnt_search;
    ArrayList();
    ll size();
    void add(ElemType data);
    ElemType get(ll i);
    ll binarySearch(ElemType k);
    ll orderSearch(ElemType k);
};
ArrayList::ArrayList() {
    index = 1;
}
ll ArrayList::size() {
    return index;
}
void ArrayList::add(ElemType data) {
    e[index++] = data;
}
ElemType ArrayList::get(ll i) {
    return e[i];
}
ll ArrayList::binarySearch(ElemType k) {
    cnt_search = 0;
    for (ll l = 1, h = index, md; l <= h;) {
        ++cnt_search;
        md = (l + h) / 2;
        if (k == e[md])
            return md;
        else if (k < e[md])
            h = md - 1;
        else
            l = md + 1;
    }
    return 0;
}
ll ArrayList::orderSearch(ElemType k) {
    cnt_search = 0;
    int i = index - 1;
    e[0] = k;
    for (; e[i] != e[0];) ++cnt_search, --i;
    e[i] == e[0] && i != 0 ? ++cnt_search : cnt_search;
    return i;
}

int main(void) {
    // 查找表1 ： { 8 ，15 ，19 ，26 ，33 ，41 ，47 ，52 ，64 ，90 }
    // 查找表2 ： {12 ，76 ，29 ，15 ，62 ，35 ，33 ，89 ，48 ，20 }
    // 查找key = 41 的比较次数：
    // 查找key = 35 的比较次数：

    ArrayList list1;
    list1.add(8);
    list1.add(15);
    list1.add(19);
    list1.add(26);
    list1.add(33);
    list1.add(41);
    list1.add(47);
    list1.add(52);
    list1.add(64);
    list1.add(90);

    cout << "index of 41: " << list1.binarySearch(41) << endl
         << "search counter of 41: " << list1.cnt_search << endl;

    ArrayList list2;
    list2.add(12);
    list2.add(76);
    list2.add(29);
    list2.add(15);
    list2.add(62);
    list2.add(35);
    list2.add(33);
    list2.add(89);
    list2.add(48);
    list2.add(20);

    cout << "index of 35: " << list2.orderSearch(35) << endl
         << "search counter of 35: " << list2.cnt_search << endl;

    return 0;
}