基于朴素贝叶斯的手写数字识别

关于数据集

MNIST数据库（http://www.cs.nyu.edu/~roweis/data.html）Google实验室的Corinna Cortes和纽约大学柯朗研究所的Yann LeCun建有一个手写数字数据库，训练库有60,000张手写数字图像，测试库有10,000张。

关于SIMD

SIMD全称Single Instruction Multiple Data，单指令多数据流，能够复制多个操作数，并把它们打包在大型寄存器的一组指令集。SIMD以同步方式，在同一时间内执行同一条指令。以加法指令为例，单指令单数据（SISD）的CPU对加法指令译码后，执行部件先访问内存，取得第一个操作数；之后再一次访问内存，取得第二个操作数；随后才能进行求和运算。而在SIMD型的CPU中，指令译码后几个执行部件同时访问内存，一次性获得所有操作数进行运算。这个特点使SIMD特别适合于多媒体应用等数据密集型运算。详细的可以看看《计算机组成原理》或者《微机原理与接口技术》

关于python

关于python里面的SIMD,我知道的主要有用于list的map,用于numpy的apply与applymap.
首先是map，这个东西我觉得很好用，而且也很简单,不过使用时往往会和lambda匿名函数一起使用，这就需要一定的练习与理解，笔者大一刚开始用的时候还不太理解，大二的时候算是入了门。大家要多多练习，不要害怕难，困难过后就是曙光。
至于apply与applymap，applymap是对整个选定行的每一个做映射，但apply是对行进行的。

数据预处理

原数据中有一些无用的信息，在计算概率之前要进行删除。

del data['__header__']
del data['__version__']
del data['__globals__']

进行数据集的划分

train={}
test={}
for x,y in data.items():
    if 'test' in x:
        test[x]=y
    else:
        train[x]=y

统计各类的先验概率

Ni=list(map(lambda x:len(x),train.values()))
s=sum(Ni)
prior_p=list(map(lambda x:x/s,Ni))
prior_p

将数据进行降维与二值化，因为训练集和测试集都要用到，所以我将其封装成了一个函数，不过这个函数的效率不是很高（不过已经比很大一部分人的快了），后来偶然发现有一个自带函数可以做这项工作，但是因为比较忙给忘了，希望看到的人可以联系笔者，我会改正的。

def im2bw(train):
    a={}
    for name in train.keys():
        a[name]=[]
    for x,y in train.items():
        for picture in y:
            index=[]
            for i in range(0,112,28):
                for j in range(0,7):
                    index.append(i+j)
            a[x].append([])
            for i in range(7):
                for j in range(4):
                    a[x][-1].append(1 if (np.sum(picture[index]>0)/28)>0 else 0)
                    index=list(map(lambda x:x+7,index))
                index=list(map(lambda x:x+84,index))
    return a

下面我说说我的二值化思路，我将其变成了74的矩阵，使用map来加快速度。这里大家可以改变其中的数值，来生成77等等的矩阵来进行下一步的运算。
下图为我老师ppt上的内容，大家可以做一个参考

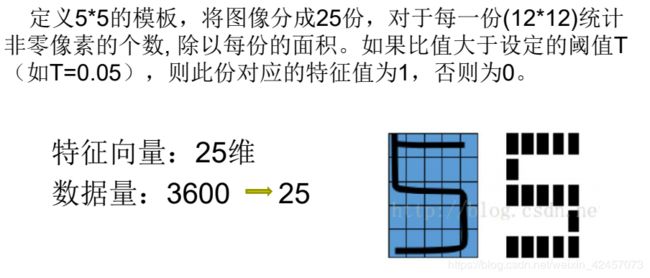
train=im2bw(train)
test=im2bw(test)

以下是平滑处理后的类条件概率计算，即


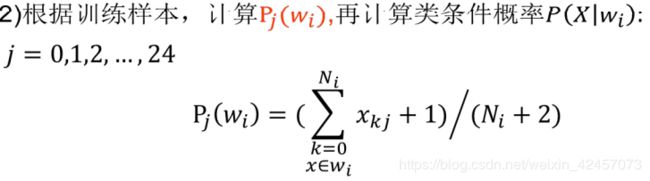
这里的平滑处理其实是很有必要的，可以提高模型的泛化性。比如当分子为0时，概率不至于为0，且当分子接近分母时，分母上的2又可以使概率不会为1，可以减少数据集过小带来的误差。当数据集很大时，1和2相对较小，可以使其更接近真实值。

s={}
for x,y in train.items():
    s[x]=(np.sum(y,axis=0)+1)/(Ni[int(x[5])]+2)
s

计算类条件概率

定义一个函数来求类条件概率

 from functools import reduce
 def class_cond_p_test(data,ccp_train):
     p=list(map(lambda x: ccp_train[x] if data[x]==1 else 1-ccp_train[x],range(0,28)))
     return reduce(lambda x,y:x*y,p)

下面求后验概率，因为只有分子不同，因此直接跳过求分母的阶段，只求分子大小即可。

ccp_test={}
for name1 in test.keys():
    ccp_test[name1]={}
    for name2 in test.keys():
        ccp_test[name1][name2]=list(map(lambda x:class_cond_p_test(x,s['train'+name2[4]])*prior_p[int(name2[4])],test[name1]))

选择后验概率最大的那个

result={}
for name in test.keys():
    df=pd.DataFrame(ccp_test[name])
    result[name]=df.idxmax(axis=1)

这里使用的是DataFrame里的idxmax函数，它可以找到每一行或者每一列最大值的下标，那么将原数据转化为DataFrame之后，就可以直接使用这个函数，并将下标+1即可得到分类结果

下面是求准确率的过程

#准确率
accuracy={}
for name in test.keys():
    accuracy[name]=sum(result[name]==name)/len(result[name])

我最后的准确率并不是太高，原因主要是两点，第一是朴素贝叶斯自身的特性，很多增强数据根本没有办法识别，第二是降维太严重，因此同学们可以在二值化时选择保留更多的细节，这样模型的效果会更好。
下面给出全部代码

import pandas as pd 
import numpy as np 
import math
import matplotlib.pyplot as plt
import re
from collections import Counter
from scipy.io import loadmat

data=loadmat(r'E:\迅雷下载\mnist_all.mat')
def im2bw(train):
    a={}
    for name in train.keys():
        a[name]=[]
    for x,y in train.items():
        for picture in y:
            index=[]
            for i in range(0,112,28):
                for j in range(0,7):
                    index.append(i+j)
            a[x].append([])
            for i in range(7):
                for j in range(4):
                    a[x][-1].append(1 if (np.sum(picture[index]>0)/28)>0 else 0)
                    index=list(map(lambda x:x+7,index))
                index=list(map(lambda x:x+84,index))
    return a
del data['__header__']
del data['__version__']
del data['__globals__']

train={}
test={}
for x,y in data.items():
    if 'test' in x:
        test[x]=y
    else:
        train[x]=y
Ni=list(map(lambda x:len(x),train.values()))
s=sum(Ni)
prior_p=list(map(lambda x:x/s,Ni))
prior_p

s={}
for x,y in train.items():
    s[x]=(np.sum(y,axis=0)+1)/(Ni[int(x[5])]+2)
s
test=im2bw(test)
 from functools import reduce
 def class_cond_p_test(data,ccp_train):
     p=list(map(lambda x: ccp_train[x] if data[x]==1 else 1-ccp_train[x],range(0,28)))
     return reduce(lambda x,y:x*y,p)

ccp_test={}
for name1 in test.keys():
    ccp_test[name1]={}
    for name2 in test.keys():
        ccp_test[name1][name2]=list(map(lambda x:class_cond_p_test(x,s['train'+name2[4]])*prior_p[int(name2[4])],test[name1]))

result={}
for name in test.keys():
    df=pd.DataFrame(ccp_test[name])
    result[name]=df.idxmax(axis=1)

#准确率
accuracy={}
for name in test.keys():
    accuracy[name]=sum(result[name]==name)/len(result[name])

总结

我的这份代码缺陷很明显，就是运行时间略微有一点长，但是80%以上的时间都是在进行二值化降维，因此如果读者有好的方法，可以提供给我，我也想尽力完善它。这是我的第一份博客，距离这份代码完成已经半年有余，没能细致讲解，还请各位谅解。遇到不懂的，大家可以一起讨论，共同进步！