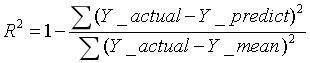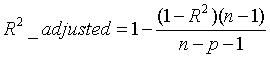（机器学习）如何评价回归模型？——Adjusted R-Square（校正决定系数）

在分类模型中，评价输出相对简单，有“错误率”、“混淆矩阵（confusion matrix）”、“正确率（precision）”、“召回率（recall）”、ROC曲线等等。但回归模型怎样评价呢？

在一个回归预测结束后得到一串预测结果Y_predict。另有真实结果Y_actual。有如下值评价：

1、SSE（误差平方和）

如果用这个，你会得到一个巨大的数，比如好几万多，你也不知道它代表什么，就知道误差很大。其实不一定，因为随着样本数增加，这个误差平方和必然跟着增大。这个数什么也不代表，除非是对比，比如两个或多个回归模型放一起比较，谁的误差平方和越小，则误差越小，则这个模型表现越好。

另外，标准线性回归模型的原理就是，通过计算使误差平方和最小。所以用它来表示误差理所应当。

（《机器学习实战》第八章P145的rssError函数即是算误差平方和，并以此评价模型效果。）
另外，有个神奇、类似但并不是的例子和此相关，那就是sklearn.cluster.KMeans的score方法（这个就不是回归了）是把x中的每个value减去同意分类中的所在维度的平均值的平均值后做平方，再把这些平方们做加和。（说它神奇是因为score(x,y)的y根本没用。）

2、R-Square（决定系数)

（此处的R即相关系数，相关系数的平方就是决定系数R-Square。）

R-Square的取值范围是“负无穷到1”，经常是“0到1”。

• 当其为1时，表示预测结果全错。
• 当其从正负方向接近0时，表示可能很正确。是可能。
• 当其为负数很大时，什么也不能表示。

大致理解为，为正数时，约接近0说明预测越正确，越接近1说明预测越不对。越大越好。

它的作用是，把“误差平方和”这个好几万的数，变成 R-Square这个（一般来说）0~1的数，还能在只有这一套样本一个模型的情况下，知道预测结果大概准不准，大概有多准。

之所以说“大概有多准”，是因为随着“样本数”增加（立个flag，下文会提到），R-Square必然增加，无法真正定量说明准确程度，只能大概定量。

3、Adjusted R-Square（校正决定系数）

其中，n为样本数量，p为特征数量。即样本为n个[ x1, x2, x3, … , xp, y ]。

这个式子其实就是将R-Square式子中那个“一堆除以一堆”乘以“一个稍大于1的数”再被1减。样本数量（接上文flag）会影响“一个稍大于1的数”，故而抵消样本数量对R-Square的影响。
做到了真正的 0~1，越大越好。

---

自己造个轮子，在python的numpy下求Adjusted R-Square（校正决定系数）的函数：

import numpy as np

def score(a,b,dimension):       
# a is predict, b is actual. dimension is len(train[0]).
    aa=a.copy(); bb=b.copy()
    if len(aa)!=len(bb):
        print('not same length')
        return np.nan

    cc=aa-bb
    wcpfh=sum(cc**2)

    # RR means R_Square
    RR=1-sum((bb-aa)**2)/sum((bb-np.mean(bb))**2)

    n=len(aa); p=dimension
    Adjust_RR=1-(1-RR)*(n-1)/(n-p-1)
    # Adjust_RR means Adjust_R_Square

    return Adjust_RR

经测试，这个函数的结果和sklearn里的score函数结果极为接近（误差千分之一）。说明那个也是用的同样原理，估计是部分参数略微不同。

---

真心是本人原创。欢迎转载，请链接注明出处。