经典排序算法的学习笔记

排序算法看多少遍忘多少遍…所以干脆记下来算了。
为了方便更清晰的认识，先看一张图：

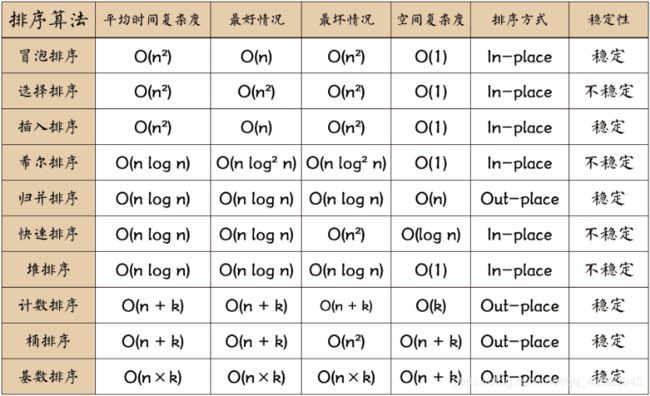
一、冒泡排序。
比较相邻元素。如果第一个比第二个大，就交换。
从第一对开始遍历，第一轮结束后，最末的元素是最大的数。
剩下的元素重复以上步骤。
输入为正序时最快O(n)，输入为反序时最慢O(n×n)。
python实现：

def bubbleSort(a):
    for i in range(1, len(a)):
        for j in range(0, len(a)-i):
            if a[j] > a[j+1]:
                a[j], a[j + 1] = a[j + 1], a[j]
    return a

二、选择排序。
首先在序列中找到最小元素，存放在序列起始位置。
再从剩余序列中继续找到最小元素，存放在已排序序列的后面。
循环重复第二步。
python实现：

def selectionSort(a):
	for i in range(len(a)-1):
	minindex=i # 记录最小数的索引
	for j in range(i+1,len(a)):
		if a[i]<a[j]:
		minindex=j
	if i != minindex: # i 不是最小数时，将 i 和最小数进行交换
		a[i],a[minindex]=a[minindex],a[i]
	return a

三、插入排序。
将序列第一个元素看成已排好的序列，后面的看成未排序序列。
从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。
python实现：

def insertionSort(a):
	for i in range(len(a)):
		pre=i-1
		value=a[i]
		while pre >= 0 and a[pre] > value:
			a[pre+1]=a[pre]
			pre -= 1
		a[pre+1]=value
	return a

四、希尔排序。
是插入排序的一种高级改进，但不稳定。
思想：先将整个待排序列分割成若干个子序列，分别进行插入排序，待子序列有序时，再对全体进行插入排序。
python实现：

import math
def shellSort(a):
	gap = 1
	while(gap < len(a)/3):
        gap = gap*3+1
    while gap > 0:
        for i in range(gap,len(a)):
            temp = a[i]
            j = i-gap
            while j >=0 and a[j] > temp:
                a[j+gap]=a[j]
                j-=gap
            a[j+gap] = temp
        gap = math.floor(gap/3)
    return arr

五、归并排序。
思想：分而治之。
python实现：

import math
def mergesort(a):
    if len(a) <= 1: 
        return a
    mid = len(a)//2
    left=a[0:mid]   #将序列不断分成子序列
    right=a[mid:]
    return merge(mergesort(left),mergesort(right))
def merge(left,right):
    i,j=0,0  #子序列的index
    result=[] #创建一个空列表接收每次比较的结果
    while i <len(left) and j <len(right):
        if left[i]<=right[j]:
            result.append(left[i])
            i+=1
        else:
            result.append(right[j])
            j+=1
    result += left[i:]
    result += right[j:] #这时剩下的一个i或者j到了序列的最后
    return result

六、快速排序。
在序列中选一个元素作为‘基准’；
所有元素依次与基准比较，小就左移，大就右移；
基准两边的序列作为新的序列，再重复上面2步骤，直到所有子序列只剩下一个元素。
python实现：

sort=lambda a: a if len(a)<=1 else sort([i for i in a[1:] if i<=a[0]])+[a[0]]+sort([i for i in a[1:] if i>a[0]])

def quick_sort(a):
    if len(a) < 2:
        return a
    mid = a[len(a) // 2]  # 选取基准，随便选哪个都可以，选中间的便于理解
    left, right = [], []  # 定义基准值左右两个数列
    arr.remove(mid)   # 从原始数组中移除基准值
    for i in a:
        if i >= mid:  # 大于基准值放右边
            right.append(i)
        else:         # 小于基准值放左边
            left.append(i)
    return quick_sort(left) + [mid] + quick_sort(right)

归并排序与快排两种排序思想都是分而治之，但是它们分解和合并的策略不一样：
归并是从中间直接将数列分成两个，而快排是比较后将小的放左边大的放右边，所以在合并的时候归并排序还是需要将两个数列重新再次排序，而快排则是直接合并不再需要排序，所以快排比归并排序更高效一些。
优化：对大规模数据集进行快排，当分区的规模达到一定小时改用插入排序，插入排序在小数据规模时排序性能较好。