Tensorflow2.0学习（3）：数据的归一化与回调函数的使用

数据归一化的作用

• 可以加快梯度下降求解最优解的速度，减少迭代次数。
• 可以在一定程度上提高模型的训练效果：将不同数据的特征映射到同一维度上，防止有些数据的特征占主导。

回调函数的作用与使用简单说明

• 回调函数是人与机器的一种很好的交互方式，可在训练过程中对epoch结果进行判断，而不必等到训练完成再判断。
• 一些常见的回调函数：
  • keras.callbacks.EarlyStopping:在监视到训练的质量改变不大时停止训练。常用参数：
    • monitor：观测质量的指标
    • min_delta：监测质量指标的最小改变值
    • patience：设定在几个epoch后观测指标没有改善，就停止训练
  • keras.callbacks.ModelCheckpoint：在每一个epoch后保存模型，也就是在一个地方保存模型的权重矩阵。常用参数：
    • filepath：保存模型文件的地址
    • save_best_only：当它为True时，最近一次最好的模型被保存且不会被其他不好的模型覆盖。
  • keras.callbacks.TensorBoard：将tensorboard可视化。常用参数：
    • log_dir：保存的路径
  • keras.callbacks.ReduceLROnPlateau：当指标停止改善的时候，改变学习率
    • monitor：观测质量的指标
    • factor：改变率，若factor=0.1，则new_l = old_l * 0.1
    • patience：设定在几个epoch后观测指标没有改善，就改变学习率

在之前的代码中增添归一化与回调函数

• 在上一篇中，得到初始的训练数据、验证数据、测试数据后，对数据进行归一化处理：

# 归一化处理：x = (x - u)/std :减去均值除以方差

from sklearn.preprocessing import StandardScaler
# 初始化一个StandarScaler对象
scaler = StandardScaler()
# fit_transform要求为二维矩阵，因此需要先转换
# 要进行除法，因此先转化为浮点型
# x_train是三维矩阵[None,28,28]，先将其转换为二维矩阵[None,784],再将其转回三维矩阵
# reshape（-1， 1）转化为一列(-1代表不确定几行)
# fit: 求得训练集的均值、方差、最大值、最小值等训练集固有的属性
# transform: 在fit的基础上，进行标准化，降维，归一化等操作
x_train_scaled = scaler.fit_transform(
    x_train.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28)
x_valid_scaled = scaler.transform(x_valid.astype(np.float32).reshape(
    -1, 1)).reshape(-1, 28, 28)
x_test_scaled = scaler.transform(x_test.astype(np.float32).reshape(
    -1, 1)).reshape(-1, 28, 28)

• 构建模型

# tf.keras.models.Sequential() 构建模型

# 创建一个Sequential的对象,顺序模型，多个网络层的线性堆叠
# 可使用add方法将各层添加到模块中
model = keras.models.Sequential()

# 添加层次
# 输入层：Flatten将28*28的图像矩阵展平成为一个一维向量
model.add(keras.layers.Flatten(input_shape=[28, 28]))

# 全连接层（上层所有单元与下层所有单元都连接）：
# 第一层300个单元，第二层100个单元，激活函数为 relu:
# relu: y = max(0, x)
model.add(keras.layers.Dense(300, activation="relu"))
model.add(keras.layers.Dense(100, activation="relu"))

# 输出为长度为10的向量，激活函数为 softmax:
# softmax: 将向量变成概率分布，x = [x1, x2, x3],
# y = [e^x1/sum, e^x2/sum, e^x3/sum],sum = e^x1+e^x2+e^x3
model.add(keras.layers.Dense(10, activation="softmax"))

# 目标函数的构建与求解方法
# 为什么使用sparse? :
# y->是一个数，要用sparse_categorical_crossentropy
# y->是一个向量，直接用categorical_crossentropy
model.compile(loss="sparse_categorical_crossentropy",
              optimizer="adam",
              metrics=["accuracy"])
"""
构建模型也可以这样：
model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28,28]),
    keras.layers.Dense(300,activation="relu"),
    keras.layers.Dense(300,activation="relu"),
    keras.layers.Dense(10,activation="softmax")
])
"""   

• 增加回调函数

# 开启训练
# epochs:训练集遍历10次
# validation_data:每隔一段时间就会验证集验证
# 会发现loss和accuracy到后面一直不变，因为用sgd梯度下降法会导致陷入局部最小值点
# 因此将loss函数的下降方法改为 adam

# callbcaks:回调函数，在每次迭代之后自动调用一些进程，如判断loss值是否达到要求
# 因此callbacks需要加在训练的过程中，即加在fit中
# 此处使用 Tensorboard, earlystopping, ModelCheckpoint 回调函数

# Tensorboard需要一个文件夹，ModelCheckpoint需要一个文件名
# 因此先创建一个文件夹和文件名

logdir = os.path.join("callbacks")
if not os.path.exists(logdir):
    os.mkdir(logdir)
# 在callbacks文件夹下创建文件。c=os.path.join(a,b),c=a/b
output_model_file = os.path.join(logdir, "fashion_mnist_model.h5")

callbacks = [
    keras.callbacks.TensorBoard(log_dir=logdir),
    keras.callbacks.ModelCheckpoint(output_model_file, save_best_only=True),
    keras.callbacks.EarlyStopping(patience=5, min_delta=1e-3),
]
history = model.fit(x_train_scaled,
                    y_train,
                    epochs=10,
                    validation_data=(x_valid_scaled, y_valid),
                    callbacks=callbacks)
# 查看tensorboard:
# 1.在所在的环境下，进入callbacks文件夹所在的目录
# 2.输入：tensorboard --logdir="callbacks"
# 3.打开浏览器：输入localhost:(端口号)

Train on 55000 samples, validate on 5000 samples
Epoch 1/10
   32/55000 [..............................] - ETA: 33:43 - loss: 2.7747 - accuracy: 0.0625WARNING:tensorflow:Method (on_train_batch_end) is slow compared to the batch update (0.107569). Check your callbacks.
55000/55000 [==============================] - 9s 172us/sample - loss: 0.4575 - accuracy: 0.8336 - val_loss: 0.3593 - val_accuracy: 0.8728
Epoch 2/10
55000/55000 [==============================] - 8s 139us/sample - loss: 0.3522 - accuracy: 0.8704 - val_loss: 0.3343 - val_accuracy: 0.8802
Epoch 3/10
55000/55000 [==============================] - 8s 152us/sample - loss: 0.3180 - accuracy: 0.8812 - val_loss: 0.3289 - val_accuracy: 0.8816
Epoch 4/10
55000/55000 [==============================] - 8s 139us/sample - loss: 0.2929 - accuracy: 0.8909 - val_loss: 0.3305 - val_accuracy: 0.8838
Epoch 5/10
55000/55000 [==============================] - 7s 132us/sample - loss: 0.2744 - accuracy: 0.8963 - val_loss: 0.3458 - val_accuracy: 0.8814
Epoch 6/10
55000/55000 [==============================] - 7s 130us/sample - loss: 0.2566 - accuracy: 0.9043 - val_loss: 0.3298 - val_accuracy: 0.8870
Epoch 7/10
55000/55000 [==============================] - 7s 134us/sample - loss: 0.2436 - accuracy: 0.9089 - val_loss: 0.3166 - val_accuracy: 0.8892
Epoch 8/10
55000/55000 [==============================] - 7s 133us/sample - loss: 0.2299 - accuracy: 0.9133 - val_loss: 0.3098 - val_accuracy: 0.8864
Epoch 9/10
55000/55000 [==============================] - 7s 132us/sample - loss: 0.2170 - accuracy: 0.9187 - val_loss: 0.3288 - val_accuracy: 0.8876
Epoch 10/10
55000/55000 [==============================] - 7s 131us/sample - loss: 0.2112 - accuracy: 0.9208 - val_loss: 0.3308 - val_accuracy: 0.8880

• 训练结果

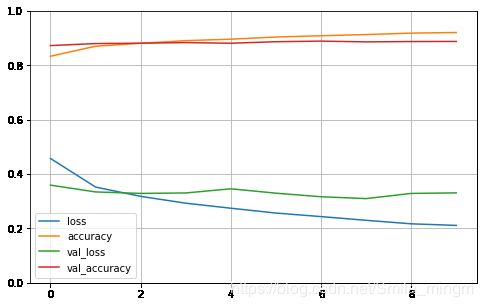
def plot_learning_curves(history):
    # 将history.history转换为dataframe格式
    pd.DataFrame(history.history).plot(figsize=(8, 5))
    plt.grid(True)
    # gca：get current axes,gcf: get current figure
    plt.gca().set_ylim(0, 1)
    plt.show()


plot_learning_curves(history)

• 模型的测试

model.evaluate(x_test_scaled, y_test, verbose=2)
# evaluate 中的 verbose:
# verbose：日志显示
# verbose = 0 为不在标准输出流输出日志信息
# verbose = 1 为输出进度条记录
# 只能取 0 和 1；默认为 1

10000/1 - 1s - loss: 0.2266 - accuracy: 0.8798


[0.36443468630313874, 0.8798]