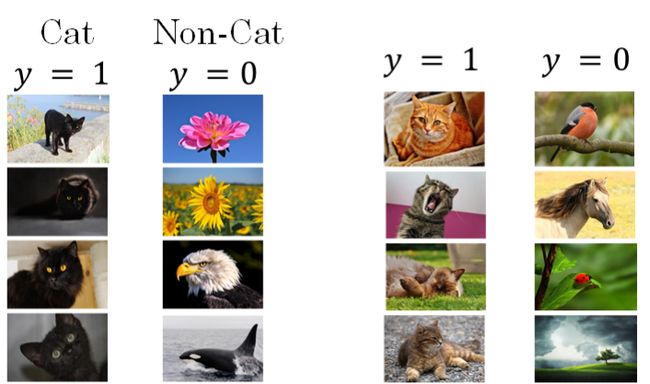吴恩达深度学习第二课笔记——改善深层神经网络：超参数调试、正则化以及优化

第一周：深度学习的实践层面(Practical aspects of Deep Learning)

1.1 训练，验证，测试集（Train / Dev / Test sets）

选择最佳的训练集（Training sets）、验证集（Development sets）、测试集（Test sets）对神经网络的性能影响非常重要。除此之外，在构建一个神经网络的时候，我们需要设置许多参数，例如神经网络的层数、每个隐藏层包含的神经元个数、学习因子（学习速率）、激活函数的选择等等。

实际上很难在第一次设置的时候就选择到这些最佳的参数，而是需要通过不断地迭代更新来获得。这个循环迭代的过程是这样的：我们先有个想法 Idea，先选择初始的参数值，构建神经网络模型结构；然后通过代码 Code 的形式，实现这个神经网络；最后，通过实验 Experiment 验证这些参数对应的神经网络的表现性能。根据验证结果，我们对参数进行适当的调整优化，再进行下一次的 Idea->Code->Experiment 循环。通过很多次的循环，不断调整参数，选定最佳的参数值，从而让神经网络性能最优化。

深度学习已经应用于许多领域中，比如 NLP，CV，Speech Recognition 等等。通常来说，最适合某个领域的深度学习网络往往不能直接应用在其它问题上。**解决不同问题的最佳选择是根据样本数量、输入特征数量和电脑配置信息（GPU或者CPU）等，来选择最合适的模型。**即使是最有经验的深度学习专家也很难第一次就找到最合适的参数。因此，应用深度学习是一个反复迭代的过程，需要通过反复多次的循环训练得到最优化参数。决定整个训练过程快慢的关键在于单次循环所花费的时间，单次循环越快，训练过程越快。而设置合适的 Train/Dev/Test sets 数量，能有效提高训练效率。

一般地，我们将所有的样本数据分成三个部分：

• Train sets用来训练你的算法模型
• Dev sets用来验证不同算法的表现情况，从中选择最好的算法模型
• Test sets用来测试最好算法的实际表现，作为该算法的无偏估计

之前人们通常设置 Train sets 和 Test sets 的数量比例为 70% 和 30%。如果有 Dev sets，则设置比例为 60%、20%、20%，分别对应 Train/Dev/Test sets。这种比例分配在样本数量不是很大的情况下，例如100,1000,10000，是比较科学的。但是随着数据量不断变大，样本数据量越大，相应的 Dev/Test sets 的比例可以设置的越低一些。

因为 Dev sets的目标是用来比较验证不同算法的优劣，Test sets 目标是测试已选算法的实际表现，不需要特别大的数据量即可验证。

现代深度学习还有个重要的问题就是训练样本和测试样本分布上不匹配，意思是训练样本和测试样本来自于不同的分布。解决这一问题的比较科学的办法是尽量保证 Dev sets 和 Test sets 来自于同一分布。值得一提的是，训练样本非常重要，通常我们可以将现有的训练样本做一些处理，例如图片的翻转、假如随机噪声等，来扩大训练样本的数量，从而让该模型更加强大。即使 Train sets 和 Dev/Test sets 不来自同一分布，使用这些技巧也能提高模型性能。

通过 transfer learning 提高模型的泛化能力

最后提一点的是如果没有 Test sets 也是没有问题的。Test sets 的目标主要是进行无偏估计。我们可以通过 Train sets 训练不同的算法模型，然后分别在 Dev sets 上进行验证，根据结果选择最好的算法模型。这样也是可以的，不需要再进行无偏估计了。如果只有 Train sets 和 Dev sets，通常也有人把这里的 Dev sets 称为 Test sets，我们要注意加以区别。

1.2 偏差，方差（Bias /Variance）

偏差（Bias）和方差（Variance）是机器学习领域非常重要的两个概念和需要解决的问题。在传统的机器学习算法中，Bias 和 Variance 是对立的，分别对应着欠拟合和过拟合，我们常常需要在 Bias 和 Variance 之间进行权衡。而在深度学习中，我们可以同时减小 Bias 和 Variance，构建最佳神经网络模型。

深度学习中，我们可以同时减小 Bias和 Variance？

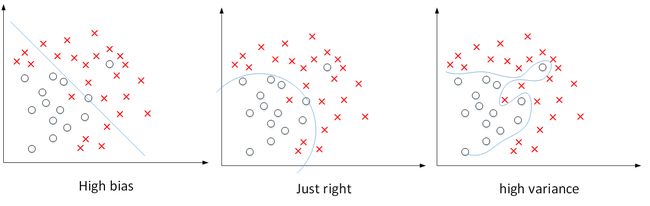
如下图所示，显示了二维平面上，high bias，just right，high variance的例子。可见，high bias对应着欠拟合，而high variance对应着过拟合。

上图这个例子中输入特征是二维的，high bias和high variance可以直接从图中分类线看出来。而对于输入特征是高维的情况，如何来判断是否出现了high bias或者high variance呢？

基准错误是 0%，上面四种分别对应高方差、高偏差、高偏差高方差、低偏差低方差

一般来说，Train set error体现了是否出现bias，Dev set error体现了是否出现variance（正确地说，应该是Dev set error与Train set error的相对差值）。

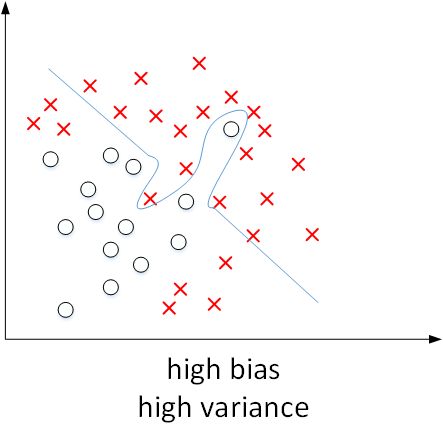
我们已经通过二维平面展示了high bias或者high variance的模型，下图展示了high bias and high variance的模型：

模型既存在high bias也存在high variance，可以理解成某段区域是欠拟合的，某段区域是过拟合的。

李宏毅机器学习对于 bias/variance 的解释

• ​$f^{\ast }$ 的期望值 $\overline{f} $ 与靶心之间的距离就是 Bias。通俗的说，就是你没有瞄准到靶心。estimator 与靶心之间有 bias
• 你瞄准的点与 $\overline{f}$ 之间的距离就是 Variance。通俗的说，就是在瞄准的点附近射偏了

1.3 机器学习基础（Basic Recipe for Machine Learning）

上节课我们讲的是如何通过训练误差和验证集误差判断算法偏差或方差是否偏高，帮助我们更加系统地在机器学习中运用这些方法来优化算法性能。

下图就是我在训练神经网络用到的基本方法：（尝试这些方法，可能有用，可能没用）

偏差高

减少 high bias 的方法通常是增加神经网络的隐藏层个数、神经元个数，训练时间延长，选择其它更复杂的 NN 模型等。在 base error 不高的情况下，一般都能通过这些方式有效降低和避免 high bias，至少在训练集上表现良好。

方差高

减少 high variance 的方法通常是增加训练样本数据，进行正则化 Regularization。

同时减少方差和偏差

如果能找到更合适的神经网络框架，有时它可能会一箭双雕，同时减少方差和偏差。如何实现呢？想系统地说出做法很难，总之就是不断重复尝试，直到找到一个低偏差，低方差的框架，这时你就成功了。

有两点需要大家注意

1. 高偏差和高方差是两种不同的情况，我们后续要尝试的方法也可能完全不同，我通常会用训练验证集来诊断算法是否存在偏差或方差问题，然后根据结果选择尝试部分方法。举个例子，如果算法存在高偏差问题，准备更多训练数据其实也没什么用处，至少这不是更有效的方法，所以大家要清楚存在的问题是偏差还是方差，还是两者都有问题，明确这一点有助于我们选择出最有效的方法。
2. 在机器学习的初期阶段，关于所谓的偏差方差权衡的讨论屡见不鲜，原因是我们能尝试的方法有很多。可以增加偏差，减少方差，也可以减少偏差，增加方差，但是在深度学习的早期阶段，我们没有太多工具可以做到只减少偏差或方差却不影响到另一方。

但在当前的深度学习和大数据时代，只要持续训练一个更大的网络，只要准备了更多数据，那么也并非只有这两种情况，我们假定是这样，那么，只要正则适度，通常构建一个更大的网络便可以，在不影响方差的同时减少偏差，而采用更多数据通常可以在不过多影响偏差的同时减少方差。这两步实际要做的工作是：训练网络，选择网络或者准备更多数据，现在我们有工具可以做到在减少偏差或方差的同时，不对另一方产生过多不良影响。

为什么传统机器学习算法增加数据量无法达到一个基本不变另一个减少的情况？

Bias 和 Variance 的折中 tradeoff。传统机器学习算法中，Bias 和 Variance 通常是对立的，减小 Bias 会增加 Variance，减小 Variance 会增加 Bias。而在现在的深度学习中，通过使用更复杂的神经网络和海量的训练样本，一般能够同时有效减小 Bias 和 Variance。这也是深度学习之所以如此强大的原因之一。

1.4 正则化（Regularization）

深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。

我们先来回顾一下之前介绍的 Logistic regression。采用 L2 regularization，其表达式为：

$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}_2^2$$

$$||w|{|}_2^2=\sum _{j=1}^{n_x}{w}_j^2=w^{T}w$$

这里有个问题：为什么只对 w 进行正则化而不对 b 进行正则化呢？其实也可以对 b 进行正则化。但是一般 w 的维度很大，而 b 只是一个常数。相比较来说，参数很大程度上由 w 决定，改变 b 值对整体模型影响较小。所以，一般为了简便，就忽略对 b 的正则化了。

除了 L2 regularization 之外，还有另外一只正则化方法：L1 regularization。其表达式为：

$$J(w,b)=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}_1$$

$$||w|{|}_1=\sum _{j=1}^{n_x}|w_j|$$

与 L2 regularization 相比，L1 regularization 得到的 w 更加稀疏，即很多 w 为零值。其优点是节约存储空间，因为大部分 w 为 0。然而，实际上 L1 regularization 在解决 high variance 方面比 L2 regularization 并不更具优势。而且，L1 的在微分求导方面比较复杂。所以，一般 L2 regularization 更加常用。

L1、L2 regularization 中的 λ 就是正则化参数（超参数的一种）。可以设置 λ 为不同的值，在 Dev set 中进行验证，选择最佳的 λ。顺便提一下，在 python 中，由于 lambda 是保留字，所以为了避免冲突，我们使用 lambd 来表示 λ。

在深度学习模型中，L2 regularization 的表达式为：

$$J(w^{[1]},b^{[1]},\cdots ,w^{[L]},b^{[L]})=\frac{1}{m}\sum _{i=1}^{m}L({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}\sum _{l=1}^L||w^{[l]}|{|}^2$$

$$||w^{[l]}|{|}^2=\sum _{i=1}^{n^{[l]}}\sum _{j=1}^{n^{[l-1]}}(w_{ij}^{[l]}{)}^2$$

通常，我们把 $||w^{[l]}|{|}^2$ 称为 Frobenius 范数，记为 $||w^{[l]}|{|}_F^2$。一个矩阵的 Frobenius 范数就是计算所有元素平方和再开方，如下所示：

$$||A|{|}_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n|a_{ij}{|}^2}$$

值得注意的是，由于加入了正则化项，梯度下降算法中的 $d{w}^{[l]}$ 计算表达式需要做如下修改：

$$d{w}^{[l]}=d{w}_{before}^{[l]}+\frac{\lambda }{m}{w}^{[l]}$$

$$w^{[l]}:=w^{[l]}-\alpha \cdot d{w}^{[l]}$$

L2 regularization 也被称做 weight decay。这是因为，由于加上了正则项，$d{w}^{[l]}$ 有个增量，在更新 $w^{[l]}$ 的候，会多减去这个增量，使得 $w^{[l]}$ 比没有正则项的值要小一些。不断迭代更新，不断地减小。

KaTeX parse error: No such environment: eqnarray at position 7: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲w^{[l]} &:=&w…

其中，$(1-\alpha \frac{\lambda }{m})<1$

1.5 为什么正则化有利于预防过拟合呢？（Why regularization reduces overfitting?）

例子1

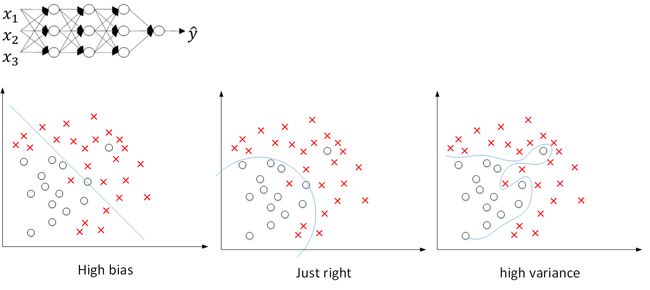
还是之前那张图，从左到右，分别表示了欠拟合，刚好拟合，过拟合三种情况。

假如我们选择了非常复杂的神经网络模型，如上图左上角所示。在未使用正则化的情况下，我们得到的分类超平面可能是类似上图右侧的过拟合。但是，如果使用 L2 regularization，当 λ 很大时，$w^{[l]}\approx 0$。$w^{[l]}$ 近似为零，意味着该神经网络模型中的某些神经元实际的作用很小，可以忽略。从效果上来看，其实是将某些神经元给忽略掉了。这样原本过于复杂的神经网络模型就变得不那么复杂了，而变得非常简单化了。如下图所示，整个简化的神经网络模型变成了一个逻辑回归模型。问题就从 high variance 变成了 high bias 了。

因此，选择合适大小的 λ 值，就能够同时避免 high bias 和 high variance，得到 just right 模型。

例子2

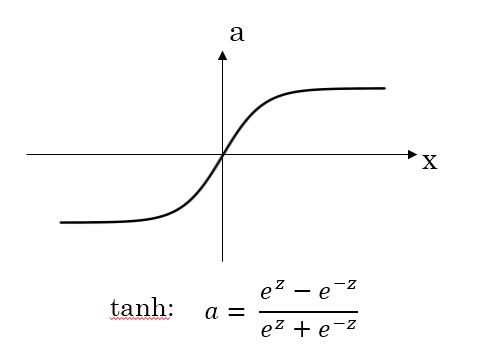
还有另外一个直观的例子来解释为什么正则化能够避免发生过拟合。假设激活函数是 tanh 函数。tanh 函数的特点是在 z 接近零的区域，函数近似是线性的，而当 |z| 很大的时候，函数非线性且变化缓慢。当使用正则化，λ 较大，即对权重 $w^{[l]}$ 的惩罚较大，$w^{[l]}$ 减小。因为 $z^{[l]}=w^{[l]}{a}^{[l]}+b^{[l]}$。当 $w^{[l]}$ 减小的时候$z^{[l]}$ 也会减小。则此时的 $z^{[l]}$ 分布在 tanh 函数的近似线性区域。那么这个神经元起的作用就相当于是 linear regression。如果每个神经元对应的权重 $w^{[l]}$ 都比较小，那么整个神经网络模型相当于是多个 linear regression 的组合，即可看成一个 linear network。得到的分类超平面就会比较简单，不会出现过拟合现象。

1.6 dropout 正则化（Dropout Regularization）

除了 L2 regularization 之外，还有另外一种防止过拟合的有效方法：Dropout

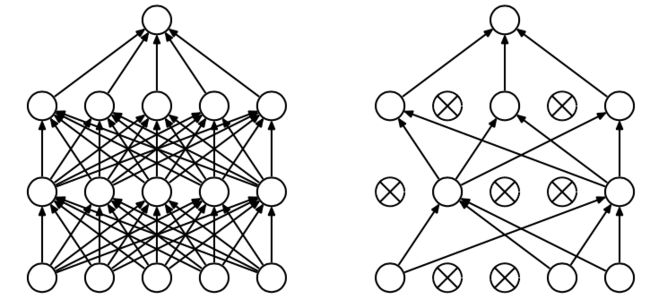
Dropout 是指在深度学习网络的训练过程中，对于每层的神经元，按照一定的概率将其暂时从网络中丢弃。也就是说，每次训练时，每一层都有部分神经元不工作，起到简化复杂网络模型的效果，从而避免发生过拟合。

Dropout 有不同的实现方法，接下来介绍一种常用的方法：Inverted dropout。假设对于第ll层神经元，设定保留神经元比例概率 keep_prob=0.8，即该层有 20% 的神经元停止工作。dl 为 dropout 向量，设置 dl 为随机 vector，其中 80% 的元素为 1，20% 的元素为 0。在 python 中可以使用如下语句生成 dropout vector：

dl = np.random.rand(al.shape[0],al.shape[1])

然后，第 l 层经过 dropout，随机删减 20% 的神经元，只保留 80% 的神经元，其输出为：

al = np.multiply(al,dl)

最后，还要对 al 进行 scale up 处理，即：

al /= keep_prob

以上就是 Inverted dropout 的方法。之所以要对 al 进行 scale up 是为了保证在经过 dropout 后，al 作为下一层神经元的输入值尽量保持不变。假设第 l 层有 50 个神经元，经过 dropout 后，有 10 个神经元停止工作，这样只有 40 神经元有作用。那么得到的 al 只相当于原来的 80%。scale up 后，能够尽可能保持 al 的期望值相比之前没有大的变化。

Inverted dropout 的另外一个好处就是在对该 dropout 后的神经网络进行测试时能够减少 scaling 问题。因为在训练时，使用 scale up 保证 $a^{[l]}$ 的期望值没有大的变化，测试时就不需要再对样本数据进行类似的尺度伸缩操作了。

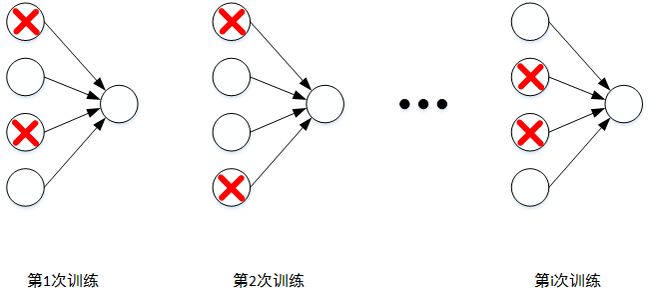
对于 m 个样本，单次迭代训练时，随机删除掉隐藏层一定数量的神经元；然后，在删除后的剩下的神经元上正向和反向更新权重 w 和常数项 b；接着，下一次迭代中，再恢复之前删除的神经元，重新随机删除一定数量的神经元，进行正向和反向更新 w 和 b。不断重复上述过程，直至迭代训练完成。

值得注意的是，使用 dropout 训练结束后，在测试和实际应用模型时，不需要进行 dropout 和随机删减神经元，所有的神经元都在工作。

1.7 理解 dropout（Understanding Dropout）

产生收缩权重的平方范数的效果

**Dropout **可以随机删除网络中的神经单元，直观上理解：不要依赖于任何一个特征，因为该单元的输入可能随时被清除，因此该单元通过这种方式传播下去，并为单元的四个输入增加一点权重，通过传播所有权重，**dropout **将产生收缩权重的平方范数的效果，和之前讲的 L2 正则化类似；实施 dropout 的结果实它会压缩权重，并完成一些预防过拟合的外层正则化；L2 对不同权重的衰减是不同的，它取决于激活函数倍增的大小。

除此之外，还可以从权重 w 的角度来解释为什么 dropout 能够有效防止过拟合。对于某个神经元来说，某次训练时，它的某些输入在 dropout 的作用被过滤了。而在下一次训练时，又有不同的某些输入被过滤。经过多次训练后，某些输入被过滤，某些输入被保留。这样，该神经元就不会受某个输入非常大的影响，影响被均匀化了。也就是说，对应的权重 w 不会很大。这从从效果上来说，与 L2 regularization 是类似的，都是对权重 w 进行“惩罚”，减小了 w 的值。

总结一下，对于同一组训练数据，利用不同的神经网络训练之后，求其输出的平均值可以减少overfitting。Dropout就是利用这个原理，每次丢掉一定数量的隐藏层神经元，相当于在不同的神经网络上进行训练，这样就减少了神经元之间的依赖性，即每个神经元不能依赖于某几个其他的神经元（指层与层之间相连接的神经元），使神经网络更加能学习到与其他神经元之间的更加健壮 robust 的特征。

在使用 dropout 的时候，有几点需要注意。首先，不同隐藏层的 dropout 系数 keep_prob 可以不同。一般来说，神经元越多的隐藏层，keep_out 可以设置得小一些.，例如 0.5；神经元越少的隐藏层，keep_out 可以设置的大一些，例如 0.8，设置是 1。另外，实际应用中，不建议对输入层进行 dropout，如果输入层维度很大，例如图片，那么可以设置 dropout，但 keep_out 应设置的大一些，例如 0.8，0.9。总体来说，就是越容易出 overfitting 的隐藏层，其 keep_prob 就设置的相对小一些。没有准确固定的做法，通常可以根据 validation 进行选择。

Dropout 在电脑视觉 CV 领域应用比较广泛，因为输入层维度较大，而且没有足够多的样本数量。值得注意的是 dropout 是一种 regularization 技巧，用来防止过拟合的，最好只在需要 regularization 的时候使用 dropout。

使用dropout的时候，可以通过绘制cost function来进行debug，看看dropout是否正确执行。一般做法是，将所有层的keep_prob全设置为1，再绘制cost function，即涵盖所有神经元，看J是否单调下降。下一次迭代训练时，再将keep_prob设置为其它值。

1.8 其他正则化方法（Other regularization methods）

除了 L2 正则化和随机失活（dropout）正则化，还有几种方法可以减少神经网络中的过拟合:

数据扩增

图片识别问题中，可以对已有的图片进行水平翻转、垂直翻转、任意角度旋转、缩放或扩大等等。如下图所示，这些处理都能“制造”出新的训练样本。虽然这些是基于原有样本的，但是对增大训练样本数量还是有很有帮助的，不需要增加额外成本，却能起到防止过拟合的效果。

early stopping

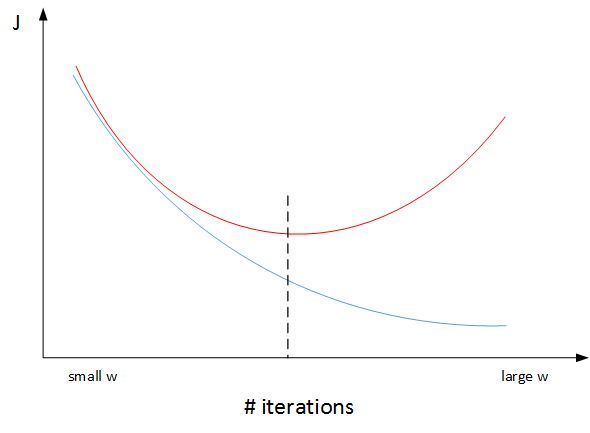
early stop 防止过拟合的思路和正则化类似，在 w 从很小到很大之间停止，这样 w 的值就不会很大而过拟合了。early stopping 只能防止过拟合，训练次数少对于损失函数是不利的，无法同时优化 Bias 和 Variance。L2 正则化可以同时优化，但是需要的计算资源更大。

一个神经网络模型随着迭代训练次数增加，train set error 一般是单调减小的，而 dev set error 先减小，之后又增大。也就是说训练次数过多时，模型会对训练样本拟合的越来越好，但是对验证集拟合效果逐渐变差，即发生了过拟合。因此，迭代训练次数不是越多越好，可以通过 train set error 和 dev set error 随着迭代次数的变化趋势，选择合适的迭代次数，即 early stopping。

然而，Early stopping 有其自身缺点。通常来说，机器学习训练模型有两个目标：一是优化 cost function，尽量减小 J；二是防止过拟合。这两个目标彼此对立的，即减小 J 的同时可能会造成过拟合，反之亦然。我们把这二者之间的关系称为正交化 orthogonalization。该节课开始部分就讲过，在深度学习中，我们可以同时减小 Bias 和 Variance，构建最佳神经网络模型。但是，Early stopping 的做法通过减少得带训练次数来防止过拟合，这样 J 就不会足够小。也就是说，early stopping 将上述两个目标融合在一起，同时优化，但可能没有“分而治之”的效果好。

与 early stopping 相比，L2 regularization 可以实现“分而治之”的效果：迭代训练足够多，减小 J，而且也能有效防止过拟合。而 L2 regularization 的缺点之一是最优的正则化参数 λ 的选择比较复杂。对这一点来说，early stopping 比较简单。总的来说，L2 regularization 更加常用一些。

1.9 归一化输入（Normalizing inputs）

进行归一化之后参数属于同一量级，可以设置较大的学习率提高训练速度。未归一化之前因为参数相差很大，需要用很小的学习率才能保证损失函数单调递减，训练速度缓慢。

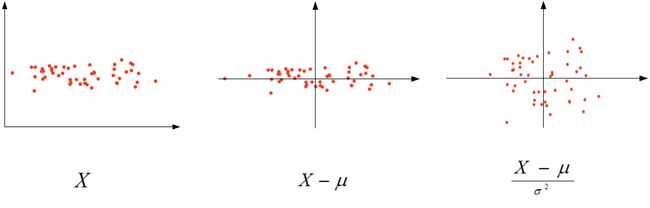
在训练神经网络时，标准化输入可以提高训练的速度。标准化输入就是对训练数据集进行归一化的操作，即将原始数据减去其均值 μ 后，再除以其方差 ${\sigma }^2$：

$$\mu =\frac{1}{m}\sum _{i=1}^m{X}^{(i)}$$

$${\sigma }^2=\frac{1}{m}\sum _{i=1}^m(X^{(i)}{)}^2$$

$$X:=\frac{X-\mu }{{\sigma }^2}$$

值得注意的是，由于训练集进行了标准化处理，那么对于测试集或在实际应用时，应该使用同样的 μ 和 ${\sigma }^2$ 对其进行标准化处理。这样保证了训练集合测试集的标准化操作一致。

之所以要对输入进行标准化操作，主要是为了让所有输入归一化同样的尺度上，方便进行梯度下降算法时能够更快更准确地找到全局最优解。

之所以要对输入进行标准化操作，主要是为了让所有输入归一化同样的尺度上，方便进行梯度下降算法时能够更快更准确地找到全局最优解。假如输入特征是二维的，且 x1 的范围是 [1,1000]，x2 的范围是 [0,1]。如果不进行标准化处理，x1 与 x2 之间分布极不平衡，训练得到的 w1 和 w2 也会在数量级上差别很大。这样导致的结果是 cost function 与 w 和 b 的关系可能是一个非常细长的椭圆形碗。对其进行梯度下降算法时，由于 w1 和 w2 数值差异很大，只能选择很小的学习因子 α，来避免 J 发生振荡。一旦 α 较大，必然发生振荡，J 不再单调下降。如下左图所示。

然而，如果进行了标准化操作，x1 与 x2 分布均匀，w1 和 w2 数值差别不大，得到的 cost function 与 w 和 b 的关系是类似圆形碗。对其进行梯度下降算法时，α 可以选择相对大一些，且 J 一般不会发生振荡，保证了 J 是单调下降的。如下右图所示。

另外一种情况，如果输入特征之间的范围本来就比较接近，那么不进行标准化操作也是没有太大影响的。但是，标准化处理在大多数场合下还是值得推荐的。

1.10 梯度消失/梯度爆炸（Vanishing / Exploding gradients）

在神经网络尤其是深度神经网络中存在可能存在这样一个问题：梯度消失和梯度爆炸。意思是当训练一个 层数非常多的神经网络时，计算得到的梯度可能非常小或非常大，甚至是指数级别的减小或增大。这样会让训练过程变得非常困难。

举个例子来说明，假设一个多层的每层只包含两个神经元的深度神经网络模型，如下图所示：

为了简化复杂度，便于分析，我们令各层的激活函数为线性函数，即 g(Z)=Z。且忽略各层常数项 b 的影响，令 b 全部为零。那么，该网络的预测输出 $\hat{Y}$ 为：

$$\hat{Y}=W^{[L]}{W}^{[L-1]}{W}^{[L-2]}\cdots W^{[3]}{W}^{[2]}{W}^{[1]}X$$

$$\hat{y}=W^{[1]}{\left[\begin{array}{cc}0.5& 0\\ 0& 0.5\end{array}\right]}^{(L-1)}x$$

假定后面 W 的权重想同，通过指数的作用，略大于 1 的会变得特别大，略小于 1 的会接近 0，由此引发梯度爆炸和梯度消失问题。当层数很大时，出现数值爆炸或消失。同样，这种情况也会引起梯度呈现同样的指数型增大或减小的变化。L 非常大时，例如 L=150，则梯度会非常大或非常小，引起每次更新的步进长度过大或者过小，这让训练过程十分困难。

1.11 神经网络的权重初始化（Weight Initialization for Deep NetworksVanishing / Exploding gradients）

下面介绍如何改善 Vanishing and Exploding gradients 这类问题，方法是对权重 w 进行一些初始化处理。

深度神经网络模型中，以单个神经元为例，该层（l）的输入个数为n，其输出为：

$$z=w_1{x}_1+w_2{x}_2+\cdots +w_n{x}_n$$

$$a=g(z)$$

这里忽略了常数项 b。为了让 z 不会过大或者过小，思路是让 w 与 n 有关，且 n 越大，w 应该越小才好。这样能够保证 z 不会过大。一种方法是在初始化 w 时，令其方差为 $\frac{1}{n}$。相应的 python 伪代码为：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(1/n[l-1]) 

如果激活函数是 tanh，一般选择上面的初始化方法。

如果激活函数是ReLU，权重w的初始化一般令其方差为 $\frac{2}{n}$：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1]) 

除此之外，Yoshua Bengio 提出了另外一种初始化 w 的方法，令其方差为 $\frac{2}{n^{[l-1]}{n}^{[l]}}$：

w[l] = np.random.randn(n[l],n[l-1])*np.sqrt(2/n[l-1]*n[l]) 

至于选择哪种初始化方法因人而异，可以根据不同的激活函数选择不同方法。另外，我们可以对这些初始化方法中设置某些参数，作为超参数，通过验证集进行验证，得到最优参数，来优化神经网络。

有时调优该超级参数效果一般，这并不是我想调优的首要超级参数，但我发现调优过程中产生的问题，虽然调优该参数能起到一定作用，但考虑到相比调优，其它超级参数的重要性，我通常把它的优先级放得比较低。

为什么 w 要乘方差？为什么是平方根？为什么不同的激活函数对应不用的方差？

1.12 梯度的数值逼近（Numerical approximation of gradients）

Back Propagation神经网络有一项重要的测试是梯度检查（gradient checking）。其目的是检查验证反向传播过程中梯度下降算法是否正确。该小节将先介绍如何近似求出梯度值。

双边误差公式的结果更准确。

利用微分思想，函数 f 在点 θ 处的梯度可以表示成：

$$g(\theta )=\frac{f(\theta +\epsilon )-f(\theta -\epsilon )}{2\epsilon }$$

其中，ε>0 ，且足够小。

1.13 梯度检验（Gradient checking）

介绍完如何近似求出梯度值后，我们将介绍如何进行梯度检查，来验证训练过程中是否出现 bug。

梯度检查首先要做的是分别将 $W^{[1]},b^{[1]},\cdots ,W^{[L]},b^{[L]}$ 这些矩阵构造成一维向量，然后将这些一维向量组合起来构成一个更大的一维向量 θ。这样 cost function $J(W^{[1]},b^{[1]},\cdots ,W^{[L]},b^{[L]})$ 就可以表示成 J(θ)。

然后将反向传播过程通过梯度下降算法得到的 $d{W}^{[1]},d{b}^{[1]},\cdots ,d{W}^{[L]},d{b}^{[L]}$ 按照一样的顺序构造成一个一维向量 dθ。dθ 的维度与 θ 一致。

接着利用 J(θ) 对每个${\theta }_i$ 计算近似梯度，其值与反向传播算法得到的 $d{\theta }_i$ 相比较，检查是否一致。例如，对于第 i 个元素，近似梯度为：

$$d{\theta }_{approx}[i]=\frac{J({\theta }_1,{\theta }_2,\cdots ,{\theta }_i+\epsilon ,\cdots )-J({\theta }_1,{\theta }_2,\cdots ,{\theta }_i-\epsilon ,\cdots )}{2\epsilon }$$

计算完所有 ${\theta }_i$ 的近似梯度后，可以计算 $d{\theta }_{approx}$ 与 dθ 的欧氏（Euclidean）距离来比较二者的相似度。公式如下：

$$\frac{||d{\theta }_{approx}-d\theta |{|}_2}{||d{\theta }_{approx}|{|}_2+||d\theta |{|}_2}$$

一般来说，如果欧氏距离小于 $\epsilon$ （例如 $10^{-7}）$，则表明 $d{\theta }_{approx}$ 与 dθ 越接近，即反向梯度计算是正确的，没有 bug。如果欧氏距离较大，例如 $10^{-5}$，则表明梯度计算可能出现问题，需要再次检查是否有 bug 存在。如果欧氏距离很大，例如 $10^{-3}$，甚至更大，则表明 $d{\theta }_{approx}$ 与 dθ 差别很大，梯度下降计算过程有 bug，需要仔细检查。

1.14 梯度检验应用的注意事项（Gradient Checking Implementation Notes）

在进行梯度检查的过程中有几点需要注意的地方：

• 不要在整个训练过程中都进行梯度检查，仅仅作为debug使用。
• 如果梯度检查出现错误，找到对应出错的梯度，检查其推导是否出现错误。
• 注意不要忽略正则化项，计算近似梯度的时候要包括进去。
• 梯度检查时关闭dropout，检查完毕后再打开dropout。
• 随机初始化时运行梯度检查，经过一些训练后再进行梯度检查（不常用）。

1.15 总结

回顾这一周，我们讲了如何配置训练集，验证集和测试集，如何分析偏差和方差，如何处理高偏差或高方差以及高偏差和高方差并存的问题，如何在神经网络中应用不同形式的正则化，如 L2 正则化和 dropout，还有加快神经网络训练速度的技巧，以及梯度消失和梯度爆炸的原因及解决方法，最后是梯度检验。

第二周：优化算法 (Optimization algorithms)

2.1 Mini-batch 梯度下降（Mini-batch gradient descent）

之前我们介绍的神经网络训练过程是对所有 m 个样本，称为 batch，通过向量化计算方式，同时进行的。如果 m 很大，例如达到百万数量级，训练速度往往会很慢，因为每次迭代都要对所有样本进行进行求和运算和矩阵运算。我们将这种梯度下降算法称为 Batch Gradient Descent。

为了解决这一问题，我们可以把 m 个训练样本分成若干个子集，称为 mini-batches，这样每个子集包含的数据量就小了，例如只有 1000，然后每次在单一子集上进行神经网络训练，速度就会大大提高。这种梯度下降算法叫做 Mini-batch Gradient Descent。

假设总的训练样本个数 m=5000000，其维度为 $(n_x,m)$。将其分成 5000 个子集，每个 mini-batch 含有 1000 个样本。我们将每个 mini-batch 记为 $X^{\{t\}}$，其维度为 $(n_x,1000)$。相应的每个 mini-batch 的输出记为 $Y^{\{t\}}$，其维度为 (1,1000)，且 t=1,2,⋯,5000

这里顺便总结一下我们遇到的神经网络中几类字母的上标含义：

• $X^{(i)}$ ：第 i 个样本
• $Z^{[l]}$ ：神经网络第 l 层网络的线性输出
• $X^{\{t\}},Y^{\{t\}}$ ：第 t 组 mini-batch

Mini-batches Gradient Descent 的实现过程是先将总的训练样本分成 T 个子集（mini-batches），然后对每个 mini-batch 进行神经网络训练，包括 Forward Propagation，Compute Cost Function，Backward Propagation，循环至 T 个 mini-batch 都训练完毕。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wQmh44Ic-1587471331030)(assets/1586851868654.png)]

经过 T 次循环之后，所有 m 个训练样本都进行了梯度下降计算。这个过程，我们称之为经历了一个 epoch。对于 Batch Gradient Descent 而言，一个 epoch 只进行一次梯度下降算法；而 Mini-Batches Gradient Descent，一个 epoch 会进行 T 次梯度下降算法。

值得一提的是，对于 Mini-Batches Gradient Descent，可以进行多次 epoch 训练。而且，每次 epoch，最好是将总体训练数据重新打乱、重新分成 T 组 mini-batches，这样有利于训练出最佳的神经网络模型。

2.2 理解 mini-batch 梯度下降法（Understanding mini-batch gradient descent）

mini-batch 是介于 SGD 和 gradient descent 之间的选择，既可以避免样本太多训练速度慢，也可以避免单个样本震荡无法达到最小值、用不到向量化提高训练速度的问题。mini-batch size 是一个超参数，需要探索设置。

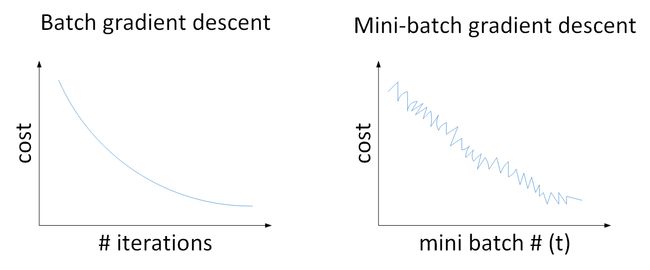
Batch gradient descent 和 Mini-batch gradient descent 的 cost 曲线如下图所示：

对于一般的神经网络模型，使用 Batch gradient descent，随着迭代次数增加，cost 是不断减小的。然而，使用 Mini-batch gradient descent，随着在不同的 mini-batch 上迭代训练，其 cost 不是单调下降，而是受类似 noise 的影响，出现振荡。但整体的趋势是下降的，最终也能得到较低的 cost 值。

之所以出现细微振荡的原因是不同的 mini-batch 之间是有差异的。例如可能第一个子集 $(X^{\{1\}},Y^{\{1\}})$ 是好的子集，而第二个子集 $(X^{\{2\}},Y^{\{2\}})$ 包含了一些噪声 noise。出现细微振荡是正常的。

如何选择每个 mini-batch 的大小，即包含的样本个数呢？有两个极端：如果 mini-batch size=m，即为 Batch gradient descent，只包含一个子集为 $(X^{\{1\}},Y^{\{1\}})=(X,Y)$；如果 mini-batch size=1，即为 Stachastic gradient descent，每个样本就是一个子集 $(X^{\{1\}},Y^{\{1\}})=(x^{(i)},y^{(i)})$，共有 m 个子集。

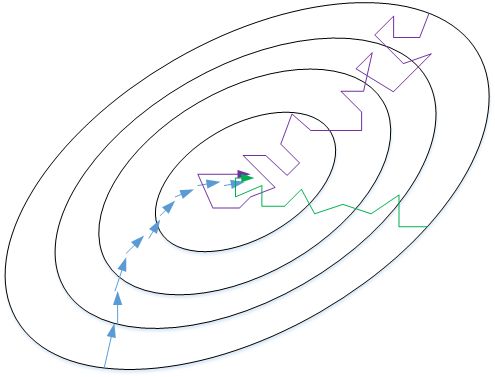
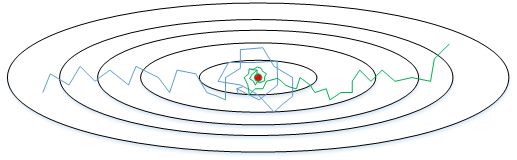
我们来比较一下 Batch gradient descent 和 Stachastic gradient descent 的梯度下降曲线。如下图所示，蓝色的线代表 Batch gradient descent，紫色的线代表 Stachastic gradient descent。Batch gradient descent 会比较平稳地接近全局最小值，但是因为使用了所有 m 个样本，每次前进的速度有些慢。Stachastic gradient descent 每次前进速度很快，但是路线曲折，有较大的振荡，最终会在最小值附近来回波动，难以真正达到最小值处。而且在数值处理上就不能使用向量化的方法来提高运算速度。

实际使用中，mini-batch size 不能设置得太大（Batch gradient descent），也不能设置得太小（Stachastic gradient descent）。这样，相当于结合了 Batch gradient descent 和 Stachastic gradient descent 各自的优点，既能使用向量化优化算法，又能叫快速地找到最小值。mini-batch gradient descent 的梯度下降曲线如下图绿色所示，每次前进速度较快，且振荡较小，基本能接近全局最小值。

一般来说，如果总体样本数量 m 不太大时，例如 m≤2000，建议直接使用 Batch gradient descent。如果总体样本数量 m 很大时，建议将样本分成许多 mini-batches。推荐常用的 mini-batch size 为 64,128,256,512。这些都是 2 的幂。之所以这样设置的原因是计算机存储数据一般是 2 的幂，这样设置可以提高运算速度。

2.3 指数加权平均数（Exponentially weighted averages）

我想向你展示几个优化算法，它们比梯度下降法快，要理解这些算法，你需要用到指数加权平均，在统计中也叫做指数加权移动平均，我们首先讲这个，然后再来讲更复杂的优化算法。

这种滑动平均算法称为指数加权平均（exponentially weighted average）。根据之前的推导公式，其一般形式为：

$$V_t=\beta V_{t-1}+(1-\beta ){\theta }_t$$

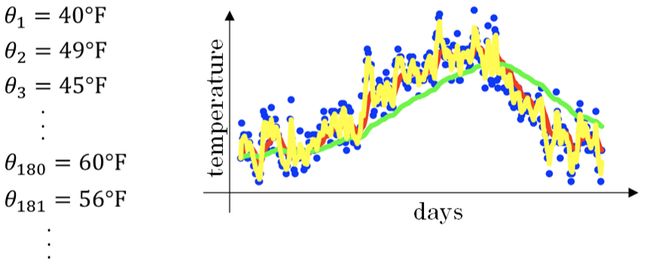
β 值决定了指数加权平均的天数，近似表示为：$\frac{1}{1-\beta }$

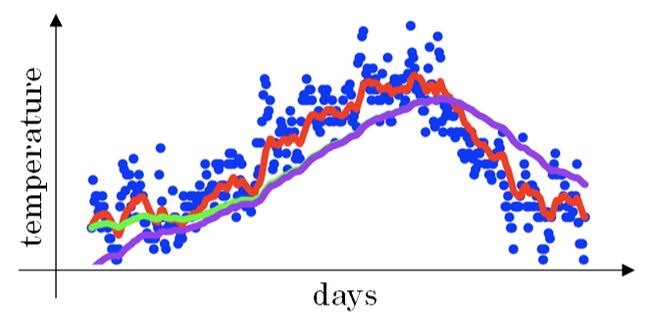
下图绿色曲线和黄色曲线分别表示了β=0.98(50天) 和 β=0.5(2天) 时，指数加权平均的结果。

这里简单解释一下公式 $\frac{1}{1-\beta }$ 是怎么来的。准确来说，指数加权平均算法跟之前所有天的数值都有关系，根据之前的推导公式就能看出。但是指数是衰减的，一般认为衰减到$\frac{1}{e}$ 就可以忽略不计了。因此，根据之前的推导公式，我们只要证明

$${\beta }^{\frac{1}{1-\beta }}=\frac{1}{e}$$

令 $\frac{1}{1-\beta }=N$， N>0，则 $\beta =1-\frac{1}{N}$ ，$\frac{1}{N}<1$。即证明转化为：

$$(1-\frac{1}{N}{)}^N=\frac{1}{e}$$

显然，当 N>>0时，上述等式是近似成立的。

2.4 理解指数加权平均数（Understanding exponentially weighted averages）

我们将指数加权平均公式的一般形式写下来：

KaTeX parse error: No such environment: eqnarray at position 7: \begin{̲e̲q̲n̲a̲r̲r̲a̲y̲}̲V_t &=&\beta V_…

观察上面这个式子，${\theta }_t,{\theta }_{t-1},{\theta }_{t-2},\cdots ,{\theta }_1$ 是原始数据值，$ (1-\beta),(1-\beta)\beta,(1-\beta)\beta^{2,\cdots,(1-\beta)\beta}{t-1}$是类似指数曲线，从右向左，呈指数下降的。VtVt 的值就是这两个子式的点乘，将原始数据值与衰减指数点乘，相当于做了指数衰减，离得越近，影响越大，离得越远，影响越小，衰减越厉害。

指数加权平均数公式的好处之一在于，它占用极少内存，电脑内存中只占用一行数字而已，然后把最新数据代入公式，不断覆盖就可以了，正因为这个原因，其效率，它基本上只占用一行代码，计算指数加权平均数也只占用单行数字的存储和内存，当然它并不是最好的，也不是最精准的计算平均数的方法。如果你要计算移动窗，你直接算出过去 10 天的总和，过去 50 天的总和，除以 10 和 50 就好，如此往往会得到更好的估测。但缺点是，如果保存所有最近的温度数据，和过去 10 天的总和，必须占用更多的内存，执行更加复杂，计算成本也更加高昂。

2.5 指数加权平均的偏差修正（Bias correction in exponentially weighted averages）

上文中提到当 β=0.98 时，指数加权平均结果如下图绿色曲线所示。但是实际上，真实曲线如紫色曲线所示。

我们注意到，紫色曲线与绿色曲线的区别是，紫色曲线开始的时候相对较低一些。这是因为开始时我们设置 $V_0=0$，所以初始值会相对小一些，直到后面受前面的影响渐渐变小，趋于正常。

修正这种问题的方法是进行偏移校正（bias correction），即在每次计算完 $V_t$ 后，对 $V_t$  进行下式处理：

$$\frac{V_t}{1-{\beta }^t}$$

在刚开始的时候，t 比较小，$(1-{\beta }^t)<1$，这样就将 $V_t$ 修正得更大一些，效果是把紫色曲线开始部分向上提升一些，与绿色曲线接近重合。随着 t 增大，$(1-{\beta }^t)\approx 1$，$V_t$ 基本不变，紫色曲线与绿色曲线依然重合。这样就实现了简单的偏移校正，得到我们希望的绿色曲线。

值得一提的是，机器学习中，偏移校正并不是必须的。因为，在迭代一次次数后（t 较大），$V_t$ 受初始值影响微乎其微，紫色曲线与绿色曲线基本重合。所以，一般可以忽略初始迭代过程，等到一定迭代之后再取值，这样就不需要进行偏移校正了。

2.6 动量梯度下降法（Gradient descent with Momentum）

动量梯度下降法通过指数加权平均处理，减小纵轴的震荡，可以用稍大的学习率更快到达最低点。

该部分将介绍动量梯度下降算法，其速度要比传统的梯度下降算法快很多。做法是在每次训练时，对梯度进行指数加权平均处理，然后用得到的梯度值更新权重 W 和常数项 b。下面介绍具体的实现过程。

原始的梯度下降算法如上图蓝色折线所示。在梯度下降过程中，梯度下降的振荡较大，尤其对于 W、b 之间数值范围差别较大的情况。此时每一点处的梯度只与当前方向有关，产生类似折线的效果，前进缓慢。而如果对梯度进行指数加权平均，这样使当前梯度不仅与当前方向有关，还与之前的方向有关，这样处理让梯度前进方向更加平滑，减少振荡，能够更快地到达最小值处。

权重 W 和常数项 b 的指数加权平均表达式如下：

$$V_{dW}=\beta \cdot V_{dW}+(1-\beta )\cdot dW$$

$$V_{db}=\beta \cdot V_{db}+(1-\beta )\cdot db$$

从动量的角度来看，以权重 W 为例，$V_{dW}$ 可以成速度 V，dW 可以看成是加速度 a。指数加权平均实际上是计算当前的速度，当前速度由之前的速度和现在的加速度共同影响。而 β<1，又能限制速度 $V_{dW}$ 过大。也就是说，当前的速度是渐变的，而不是瞬变的，是动量的过程。这保证了梯度下降的平稳性和准确性，减少振荡，较快地达到最小值处。

具体如何计算，算法在此

另外，关于偏移校正，可以不使用。因为经过 10 次迭代后，随着滑动平均的过程，偏移情况会逐渐消失。

2.7 RMSprop

RMSprop 是另外一种优化梯度下降速度的算法。每次迭代训练过程中，其权重 W 和常数项 b 的更新表达式为：

$$S_W=\beta S_{dW}+(1-\beta )d{W}^2$$

$$S_b=\beta S_{db}+(1-\beta )d{b}^2$$

$$W:=W-\alpha \frac{dW}{\sqrt{S_W}},b:=b-\alpha \frac{db}{\sqrt{S_b}}$$

下面简单解释一下 RMSprop 算法的原理，仍然以下图为例，为了便于分析，令水平方向为 W 的方向，垂直方向为 b 的方向。

从图中可以看出，梯度下降（蓝色折线）在垂直方向（b）上振荡较大，在水平方向（W）上振荡较小，表示在 b 方向上梯度较大，即 db 较大，而在 W 方向上梯度较小，即 dW 较小。因此，上述表达式中 $S_b$ 较大，而 $S_W$ 较小。

在更新 W 和 b 的表达式中，变化值 $\frac{dW}{\sqrt{S_W}}$ 较大，而 $\frac{db}{\sqrt{S_b}}$ 较小。也就使得 W 变化得多一些，b 变化得少一些。即加快了 W 方向的速度，减小了 b 方向的速度，减小振荡，实现快速梯度下降算法，其梯度下降过程如绿色折线所示。总得来说，就是如果哪个方向振荡大，就减小该方向的更新速度，从而减小振荡。

还有一点需要注意的是为了避免 RMSprop 算法中分母为零，通常可以在分母增加一个极小的常数 ε：

$$W:=W-\alpha \frac{dW}{\sqrt{S_W}+\epsilon },b:=b-\alpha \frac{db}{\sqrt{S_b}+\epsilon }$$

其中，$\epsilon =10^{-8}$，或者其它较小值。

2.8 Adam 优化算法 (Adam optimization algorithm)

Adam（Adaptive Moment Estimation）算法结合了动量梯度下降算法和 RMSprop 算法。其算法流程为：

$$V_{dW}=0,S_{dW},V_{db}=0,S_{db}=0$$

$$Oniterationt:$$

$$CimputedW,db$$

$$V_{dW}={\beta }_1{V}_{dW}+(1-{\beta }_1)dW,V_{db}={\beta }_1{V}_{db}+(1-{\beta }_1)db$$

$$S_{dW}={\beta }_2{S}_{dW}+(1-{\beta }_2)d{W}^2,S_{db}={\beta }_2{S}_{db}+(1-{\beta }_2)d{b}^2$$

$$V_{dW}^{corrected}=\frac{V_{dW}}{1-{\beta }_1^t},V_{db}^{corrected}=\frac{V_{db}}{1-{\beta }_1^t}$$

$$S_{dW}^{corrected}=\frac{S_{dW}}{1-{\beta }_2^t},S_{db}^{corrected}=\frac{S_{db}}{1-{\beta }_2^t}$$

$$W:=W-\alpha \frac{V_{dW}^{corrected}}{\sqrt{S_{dW}^{corrected}}+\epsilon },b:=b-\alpha \frac{V_{db}^{corrected}}{\sqrt{S_{db}^{corrected}}+\epsilon }$$

Adam 算法包含了几个超参数，分别是：$\alpha ,{\beta }_1,{\beta }_2,\epsilon$。其中，β1 通常设置为 0.9，β2 通常设置为 0.999，ε 通常设置为 $10^{-8}$。一般只需要对 β1 和 β2 进行调试。

实际应用中，Adam 算法结合了动量梯度下降和 RMSprop 各自的优点，使得神经网络训练速度大大提高。

2.9 学习率衰减 (Learning rate decay)

训练 epoch 越多学习率越小，减少在最优值处的震荡，更接近最优值。

减小学习因子 α 也能有效提高神经网络训练速度，这种方法被称为 learning rate decay。

Learning rate decay 就是随着迭代次数增加，学习因子 $\alpha$逐渐减小。下面用图示的方式来解释这样做的好处。下图中，蓝色折线表示使用恒定的学习因子 α，由于每次训练 $\alpha$相同，步进长度不变，在接近最优值处的振荡也大，在最优值附近较大范围内振荡，与最优值距离就比较远。绿色折线表示使用不断减小的 α，随着训练次数增加，$\alpha$ 逐渐减小，步进长度减小，使得能够在最优值处较小范围内微弱振荡，不断逼近最优值。相比较恒定的 $\alpha$ 来说，learning rate decay 更接近最优值。

Learning rate decay 中对 α 可由下列公式得到：

$$\alpha =\frac{1}{1+decay\_rate\ast epoch}{\alpha }_0$$

其中，deacy_rate 是参数（可调），epoch 是训练完所有样本的次数。随着 epoch 增加，α 会不断变小。

除了上面计算 α 的公式之外，还有其它可供选择的计算公式：

$$\alpha =0.95^{epoch}\cdot {\alpha }_0$$

$$\alpha =\frac{k}{\sqrt{epoch}}\cdot {\alpha }_{0}or\frac{k}{\sqrt{t}}\cdot {\alpha }_0$$

其中，k 为可调参数，t 为 mini-bach number。

除此之外，还可以设置 α 为关于 t 的离散值，随着 t 增加，α 呈阶梯式减小。当然，也可以根据训练情况灵活调整当前的 α 值，但会比较耗时间。

2.10 局部最优的问题 (The problem of local optima)

局部最优化问题并不像人的直观感受一样，维度更高时梯度为零的点更像是马鞍状而不是想象的局部最优

在使用梯度下降算法不断减小 cost function 时，可能会得到局部最优解（local optima）而不是全局最优解（global optima）。之前我们对局部最优解的理解是形如碗状的凹槽，如下图左边所示。但是在神经网络中，local optima 的概念发生了变化。准确地来说，大部分梯度为零的 “最优点” 并不是这些凹槽处，而是形如右边所示的马鞍状，称为 saddle point。也就是说，梯度为零并不能保证都是 convex（极小值），也有可能是 concave（极大值）。特别是在神经网络中参数很多的情况下，所有参数梯度为零的点很可能都是右边所示的马鞍状的 saddle point，而不是左边那样的 local optimum。

类似马鞍状的 plateaus 会降低神经网络学习速度。Plateaus 是梯度接近于零的平缓区域，如下图所示。在 plateaus 上梯度很小，前进缓慢，到达 saddle point 需要很长时间。到达 saddle point 后，由于随机扰动，梯度一般能够沿着图中绿色箭头，离开 saddle point，继续前进，只是在 plateaus 上花费了太多时间。

总的来说，关于 local optima，有两点总结：

• 只要选择合理的强大的神经网络，一般不太可能陷入 local optima
• Plateaus 可能会使梯度下降变慢，降低学习速度

值得一提的是，上文介绍的动量梯度下降，RMSprop，Adam 算法都能有效解决 plateaus 下降过慢的问题，大大提高神经网络的学习速度。

第三周 超参数调试、Batch 正则化和程序框架（Hyperparameter tuning）

3.1 调试处理（Tuning process）

深度神经网络需要调试的超参数（Hyperparameters）较多，包括：

α：学习因子（最重要）

β：动量梯度下降因子（次重要）

β1,β2,ε：Adam 算法参数（无需设置）

#layers：神经网络层数（次次重要）

#hidden units：各隐藏层神经元个数（次重要）

learning rate decay：学习因子下降参数（次次重要）

mini-batch size：批量训练样本包含的样本个数（次重要）

随机取值和精确搜索，考虑使用由粗糙到精细的搜索过程

如何选择和调试超参数？传统的机器学习中，我们对每个参数等距离选取任意个数的点，然后，分别使用不同点对应的参数组合进行训练，最后根据验证集上的表现好坏，来选定最佳的参数。例如有两个待调试的参数，分别在每个参数上选取 5 个点，这样构成了 5x5=25 中参数组合，如下图所示：

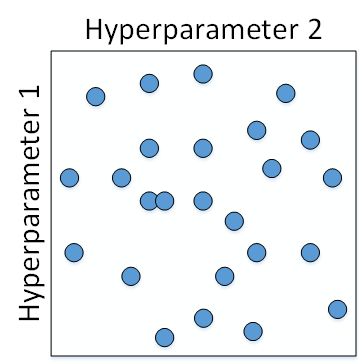
这种做法在参数比较少的时候效果较好。但是在深度神经网络模型中，我们一般不采用这种均匀间隔取点的方法，比较好的做法是使用随机选择。也就是说，对于上面这个例子，我们随机选择 25 个点，作为待调试的超参数，如下图所示：

随机化选择参数的目的是为了尽可能地得到更多种参数组合。还是上面的例子，如果使用均匀采样的话，每个参数只有 5 种情况；而使用随机采样的话，每个参数有 25 种可能的情况，因此更有可能得到最佳的参数组合。

Adam 算法中 α 比 ε 更为重要，ε 取值不怎么影响结果，所以看似 25 中选择，其实 α 只有 5 种选择

这种做法带来的另外一个好处就是对重要性不同的参数之间的选择效果更好。假设 hyperparameter1 为αα，hyperparameter2 为 ε，显然二者的重要性是不一样的。如果使用第一种均匀采样的方法，ε 的影响很小，相当于只选择了 5 个 α 值。而如果使用第二种随机采样的方法，ε 和 α 都有可能选择 25 种不同值。这大大增加了 α 调试的个数，更有可能选择到最优值。其实，在实际应用中完全不知道哪个参数更加重要的情况下，随机采样的方式能有效解决这一问题，但是均匀采样做不到这点。

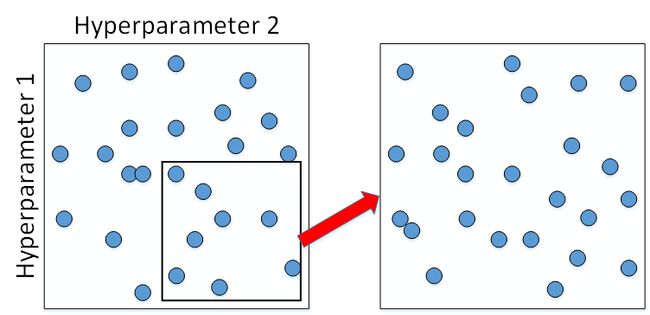
在经过随机采样之后，我们可能得到某些区域模型的表现较好。然而，为了得到更精确的最佳参数，我们应该继续对选定的区域进行由粗到细的采样（coarse to fine sampling scheme）。也就是放大表现较好的区域，再对此区域做更密集的随机采样。例如，对下图中右下角的方形区域再做 25 点的随机采样，以获得最佳参数。

3.2 为超参数选择合适的范围（Using an appropriate scale to pick hyperparameters）

上一部分讲的调试参数使用随机采样，对于某些超参数是可以进行尺度均匀采样的，但是某些超参数需要选择不同的合适尺度进行随机采样。

什么意思呢？例如对于超参数 #layers 和 #hidden units，都是正整数，是可以进行均匀随机采样的，即超参数每次变化的尺度都是一致的（如每次变化为 1，犹如一个刻度尺一样，刻度是均匀的）。

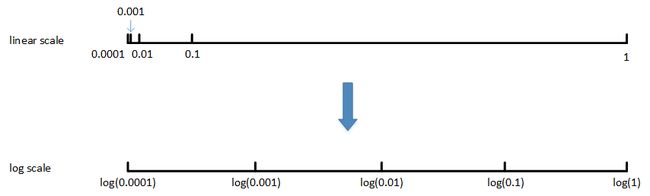
但是，对于某些超参数，可能需要非均匀随机采样（即非均匀刻度尺）。例如超参数αα，待调范围是 [0.0001, 1]。如果使用均匀随机采样，那么有 90% 的采样点分布在 [0.1, 1] 之间，只有 10% 分布在 [0.0001, 0.1] 之间。这在实际应用中是不太好的，因为最佳的 α 值可能主要分布在 [0.0001, 0.1] 之间，而 [0.1, 1] 范围内αα 值效果并不好。因此我们更关注的是区间 [0.0001, 0.1]，应该在这个区间内细分更多刻度。

通常的做法是将 linear scale 转换为 log scale，将均匀尺度转化为非均匀尺度，然后再在 log scale 下进行均匀采样。这样，[0.0001, 0.001]，[0.001, 0.01]，[0.01, 0.1]，[0.1, 1] 各个区间内随机采样的超参数个数基本一致，也就扩大了之前 [0.0001, 0.1] 区间内采样值个数。

一般解法是，如果线性区间为 [a, b]，令 m=log (a)，n=log (b)，则对应的 log 区间为 [m,n]。对 log 区间的 [m,n] 进行随机均匀采样，然后得到的采样值 r，最后反推到线性区间，即 $10^r$。$10^r$ 就是最终采样的超参数。相应的 Python 语句为：

m = np.log10(a)
n = np.log10(b)
r = np.random.rand()
r = m + (n-m)*r
r = np.power(10,r)

除了αα 之外，动量梯度因子 β 也是一样，在超参数调试的时候也需要进行非均匀采样。一般 β 的取值范围在 [0.9, 0.999] 之间，那么 1−β 的取值范围就在 [0.001, 0.1] 之间。那么直接对 1−β 在 [0.001, 0.1] 区间内进行 log 变换即可。

这里解释下为什么 β 也需要向 α 那样做非均匀采样。假设 β 从 0.9000 变化为 0.9005，那么 $\frac{1}{1-\beta }$ 基本没有变化。但假设 β 从 0.9990 变化为 0.9995，那么 $\frac{1}{1-\beta }$ 前后差别 1000。β 越接近 1，指数加权平均的个数越多，变化越大。所以对 β 接近 1 的区间，应该采集得更密集一些。

3.3 超参数调试的实践：Pandas VS Caviar（Hyperparameters tuning in practice: Pandas vs. Caviar）

经过调试选择完最佳的超参数并不是一成不变的，一段时间之后（例如一个月），需要根据新的数据和实际情况，再次调试超参数，以获得实时的最佳模型。

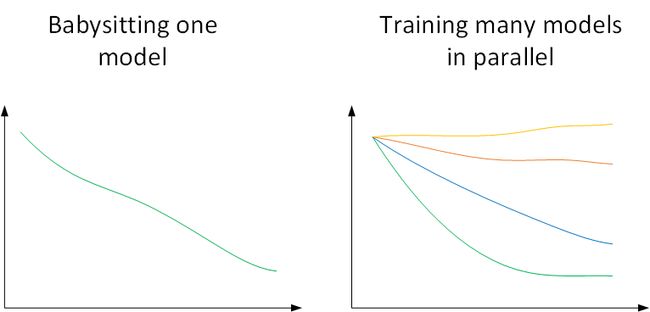
在训练深度神经网络时，一种情况是受计算能力所限，我们只能对一个模型进行训练，调试不同的超参数，使得这个模型有最佳的表现。我们称之为 Babysitting one model。另外一种情况是可以对多个模型同时进行训练，每个模型上调试不同的超参数，根据表现情况，选择最佳的模型。我们称之为 Training many models in parallel。

因为第一种情况只使用一个模型，所以类比做 Panda approach；第二种情况同时训练多个模型，类比做 Caviar approach。使用哪种模型是由计算资源、计算能力所决定的。一般来说，对于非常复杂或者数据量很大的模型，使用 Panda approach 更多一些。

3.4 归一化网络的激活函数（Normalizing activations in a network）

Sergey Ioffe 和 Christian Szegedy 两位学者提出了 Batch Normalization 方法。Batch Normalization 不仅可以让调试超参数更加简单，而且可以让神经网络模型更加 “健壮”。也就是说较好模型可接受的超参数范围更大一些，包容性更强，使得更容易去训练一个深度神经网络。接下来，我们就来介绍什么是 Batch Normalization，以及它是如何工作的。

在训练神经网络时，标准化输入可以提高训练的速度。方法是对训练数据集进行归一化的操作，即将原始数据减去其均值 μ 后，再除以其方差 ${\sigma }^2$。但是标准化输入只是对输入进行了处理，对于隐藏层也应用同样地处理，就是 Batch Normalization。值得注意的是，实际应用中，一般是对 $Z^{[l-1]}$ 进行标准化处理而不是 $A^{[l-1]}$，其实差别不是很大。

Batch Normalization 对第 l 层隐藏层的输入 $Z^{[l-1]}$做如下标准化处理，忽略上标 [l−1]：
$$\mu =\frac{1}{m}\sum _i{z}^{(i)}$$

$${\sigma }^2=\frac{1}{m}\sum _i(z_i-\mu {)}^2$$

$$z_{norm}^{(i)}=\frac{z^{(i)}-\mu }{\sqrt{{\sigma }^2+\epsilon }}$$

其中，m 是单个 mini-batch 包含样本个数，ε 是为了防止分母为零，可取值 $10^{-8}$。这样，使得该隐藏层的所有输入 $z^{(i)}$ 均值为 0，方差为 1。

但是，大部分情况下并不希望所有的 $z^{(i)}$ 均值都为 0，方差都为 1，也不太合理。通常需要对 $z^{(i)}$ 进行进一步处理：
$${\tilde{z}}^{(i)}=\gamma \cdot z_{norm}^{(i)}+\beta$$
上式中，γ 和 β 是 learnable parameters，类似于 W 和 b 一样，可以通过梯度下降等算法求得。这里，γ 和 β 的作用是让 ${\tilde{z}}^{(i)}$ 的均值和方差为任意值，只需调整其值就可以了。例如，令：
$$\gamma =\sqrt{{\sigma }^2+\epsilon },\beta =u$$
则 ${\tilde{z}}^{(i)}=z^{(i)}$，即 identity function。可见，设置 γ 和 β 为不同的值，可以得到任意的均值和方差。

这样，通过 Batch Normalization，对隐藏层的各个 $z^{[l](i)}$ 进行标准化处理，得到 ${\tilde{z}}^{[l](i)}$，替代 $z^{[l](i)}$

值得注意的是，输入的标准化处理 Normalizing inputs 和隐藏层的标准化处理 Batch Normalization 是有区别的。Normalizing inputs 使所有输入的均值为 0，方差为 1。而 Batch Normalization 可使各隐藏层输入的均值和方差为任意值。实际上，从激活函数的角度来说，如果各隐藏层的输入均值在靠近 0 的区域即处于激活函数的线性区域，这样不利于训练好的非线性神经网络，得到的模型效果也不会太好。这也解释了为什么需要用 γ 和 β 来对 $z^{[l](i)}$ 作进一步处理。

3.5 将 Batch Norm 拟合进神经网络（Fitting Batch Norm into a neural network）

我们已经知道了如何对某单一隐藏层的所有神经元进行 Batch Norm，接下来将研究如何把 Bath Norm 应用到整个神经网络中。

对于 L 层神经网络，经过 Batch Norm 的作用，整体流程如下：

实际上，Batch Norm 经常使用在 mini-batch 上，这也是其名称的由来。

无论 $b^{[l]}$ 的值是多少，都是要被减去的，因为在 Batch 归一化的过程中，你要计算 $z^{[l]}$ 的均值，再减去平均值，在此例中的 mini-batch 中增加任何常数，数值都不会改变，因为加上的任何常数都将会被均值减去所抵消。

值得注意的是，因为 Batch Norm 对各隐藏层 $Z^{[l]}=W^{[l]}{A}^{[l-1]}+b^{[l]}$ 有去均值的操作，所以这里的常数项 $b^{[l]}$ 可以消去，其数值效果完全可以由 ${\tilde{Z}}^{[l]}$ 中的 β 来实现。因此，我们在使用 Batch Norm 的时候，可以忽略各隐藏层的常数项 $b^{[l]}$。在使用梯度下降算法时，分别对 $W^{[l]}$，${\beta }^{[l]}$ 和 ${\gamma }^{[l]}$ 进行迭代更新。除了传统的梯度下降算法之外，还可以使用我们之前介绍过的动量梯度下降、RMSprop 或者 Adam 等优化算法。

3.6 Batch Norm 为什么奏效？（Why does Batch Norm work?）

我们可以把输入特征做均值为 0，方差为 1 的规范化处理，来加快学习速度。而 Batch Norm 也是对隐藏层各神经元的输入做类似的规范化处理。总的来说，Batch Norm 不仅能够提高神经网络训练速度，而且能让神经网络的权重 W 的更新更加 “稳健”，尤其在深层神经网络中更加明显。比如神经网络很后面的 W 对前面的 W 包容性更强，即前面的 W 的变化对后面 W 造成的影响很小，整体网络更加健壮。

举个例子来说明，假如用一个浅层神经网络（类似逻辑回归）来训练识别猫的模型。如下图所示，提供的所有猫的训练样本都是黑猫。然后，用这个训练得到的模型来对各种颜色的猫样本进行测试，测试的结果可能并不好。其原因是训练样本不具有一般性（即不是所有的猫都是黑猫），这种训练样本（黑猫）和测试样本（猫）分布的变化称之为 covariate shift。

对于这种情况，如果实际应用的样本与训练样本分布不同，即发生了 covariate shift，则一般是要对模型重新进行训练的。在神经网络，尤其是深度神经网络中，covariate shift 会导致模型预测效果变差，重新训练的模型各隐藏层的 $W^{[l]}$ 和 $B^{[l]}$ 均产生偏移、变化。而 Batch Norm 的作用恰恰是减小 covariate shift 的影响，让模型变得更加健壮，鲁棒性更强。**Batch Norm 减少了各层 $W^{[l]}$、$B^{[l]}$ 之间的耦合性，让各层更加独立，实现自我训练学习的效果。**也就是说，如果输入发生 covariate shift，那么因为 Batch Norm 的作用，对个隐藏层输出 $Z^{[l]}$ 进行均值和方差的归一化处理，$W^{[l]}$ 和 $B^{[l]}$ 更加稳定，使得原来的模型也有不错的表现。针对上面这个黑猫的例子，如果我们使用深层神经网络，使用 Batch Norm，那么该模型对花猫的识别能力应该也是不错的。

从另一个方面来说，Batch Norm 也起到轻微的正则化（regularization）效果。具体表现在：

• 每个 mini-batch 都进行均值为 0，方差为 1 的归一化操作
• 每个 mini-batch 中，对各个隐藏层的 $Z^{[l]}$ 添加了随机噪声，效果类似于 Dropout
• mini-batch 越小，正则化效果越明显

但是，Batch Norm 的正则化效果比较微弱，正则化也不是 Batch Norm 的主要功能。

3.7 测试时的 Batch Norm（Batch Norm at test time）

测试单个样本用的 μ 和 ${\sigma }^2$ 用估计值来计算，估计的方法为指数加权平均

训练过程中，Batch Norm 是对单个 mini-batch 进行操作的，但在测试过程中，如果是单个样本，该如何使用 Batch Norm 进行处理呢？

首先，回顾一下训练过程中 Batch Norm 的主要过程：
$$\mu =\frac{1}{m}\sum _i{z}^{(i)}$$

$${\sigma }^2=\frac{1}{m}\sum _i(z^{(i)}-\mu {)}^2$$

$$z_{norm}^{(i)}=\frac{z^{(i)}-\mu }{\sqrt{{\sigma }^2+\epsilon }}$$

$${\tilde{z}}^{(i)}=\gamma \cdot z_{norm}^{(i)}+\beta$$

其中，μ 和 ${\sigma }^2$是对单个 mini-batch 中所有 m 个样本求得的。在测试过程中，如果只有一个样本，求其均值和方差是没有意义的，就需要对 μ 和 ${\sigma }^2$ 进行估计。估计的方法有很多，理论上我们可以将所有训练集放入最终的神经网络模型中，然后将每个隐藏层计算得到的 ${\mu }^{[l]}$ 和 ${\sigma }^{2[l]}$ 直接作为测试过程的 μ和 ${\sigma }^2$ 来使用。但是，实际应用中一般不使用这种方法，而是使用我们之前介绍过的指数加权平均（exponentially weighted average）的方法来预测测试过程单个样本的 μ 和 ${\sigma }^2$。

指数加权平均的做法很简单，对于第 l 层隐藏层，考虑所有 mini-batch 在该隐藏层下的 ${\mu }^{[l]}$ 和 ${\sigma }^{2[l]}$，然后用指数加权平均的方式来预测得到当前单个样本的 ${\mu }^{[l]}$ 和 ${\sigma }^{2[l]}$。这样就实现了对测试过程单个样本的均值和方差估计。最后，再利用训练过程得到的 γ 和 β 值计算出各层的 ${\tilde{z}}^{(i)}$ 值。

3.8 Softmax 回归（Softmax regression）

目前我们介绍的都是二分类问题，神经网络输出层只有一个神经元，表示预测输出 $\hat{y}$ 是正类的概率 $P(y=1|x)$， $\hat{y}>0.5$ 则判断为正类，$\hat{y}<0.5$ 则判断为负类。

对于多分类问题，用 C 表示种类个数，神经网络中输出层就有 C 个神经元，即 $n^{[L]}=C$。其中，每个神经元的输出依次对应属于该类的概率，即 $P(y=c|x)$。为了处理多分类问题，我们一般使用 Softmax 回归模型。Softmax 回归模型输出层的激活函数如下所示：
$$z^{[L]}=W^{[L]}{a}^{[L-1]}+b^{[L]}$$

$$a_i^{[L]}=\frac{e^{z_i^{[L]}}}{{\sum }_{i=1}^C{e}^{z_i^{[L]}}}$$

输出层每个神经元的输出 $a_i^{[L]}$ 对应属于该类的概率，满足：
$$\sum _{i=1}^C{a}_i^{[L]}=1$$
所有的 $a_i^{[L]}$，即 $\hat{y}$，维度为 (C, 1)。

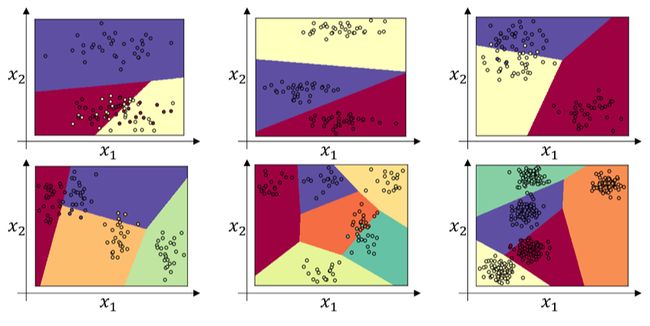
下面给出几个简单的线性多分类的例子：

如果使用神经网络，特别是深层神经网络，可以得到更复杂、更精确的非线性模型。

3.9 训练一个 Softmax 分类器（Training a Softmax classifier）

Softmax classifier 的训练过程与我们之前介绍的二元分类问题有所不同。先来看一下 softmax classifier 的 loss function。举例来说，假如 C=4，某个样本的预测输出 $\hat{y}$ 和真实输出 y 为：
$$\hat{y}=\left[\begin{array}{c}0.3\\ 0.2\\ 0.1\\ 0.4\end{array}\right]$$

$$y=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\end{array}\right]$$

从y^y值来看，P(y=4|x)=0.4，概率最大，而真实样本属于第 2 类，因此该预测效果不佳。我们定义 softmax classifier 的 loss function 为：
$$L(\hat{y},y)=-\sum _{j=1}^4{y}_j\cdot log{\hat{y}}_j$$
然而，由于只有当 j=2 时，y2=1，其它情况下，$y_j=0$。所以，上式中的 $L(\hat{y},y)$ 可以简化为：
$$L(\hat{y},y)=-y_2\cdot log{\hat{y}}_2=-log{\hat{y}}_2$$
要让 $L(\hat{y},y)$ 更小，就应该让 ${\hat{y}}_2$ 越大越好。${\hat{y}}_2$ 反映的是概率，完全符合我们之前的定义。

所有 m 个样本的 cost function 为：
$$J=\frac{1}{m}\sum _{i=1}^{m}L(\hat{y},y)$$
其预测输出向量 $A^{[L]}$ 即 $\hat{Y}$ 的维度为 (4, m)。

softmax classifier 的反向传播过程仍然使用梯度下降算法，其推导过程与二元分类有一点点不一样。因为只有输出层的激活函数不一样，我们先推导 $d{Z}^{[L]}$：
$$d{z}^{[l]}=\hat{y}-y$$

3.10 深度学习框架（Deep Learning frameworks）

深度学习框架有很多，例如：

• Caffe/Caffe2
• CNTK
• DL4J
• Keras
• Lasagne
• mxnet
• PaddlePaddle
• TensorFlow
• Theano
• Torch

一般选择深度学习框架的基本准则是：

• Ease of programming(development and deployment)
• Running speed
• Truly open(open source with good governance)

3.11 TensorFlow

TensorFlow 的最大优点就是采用数据流图（data flow graphs）来进行数值运算。图中的节点（Nodes）表示数学操作，图中的线（edges）则表示在节点间相互联系的多维数据数组，即张量（tensor）。而且它灵活的架构让你可以在多种平台上展开计算，例如台式计算机中的一个或多个 CPU（或 GPU），服务器，移动设备等等。

参考链接

b 站视频

视频文稿

红色石头笔记