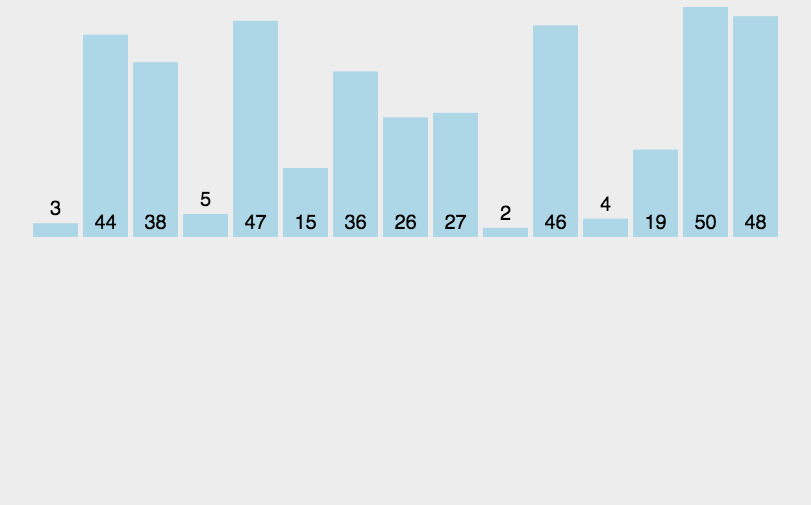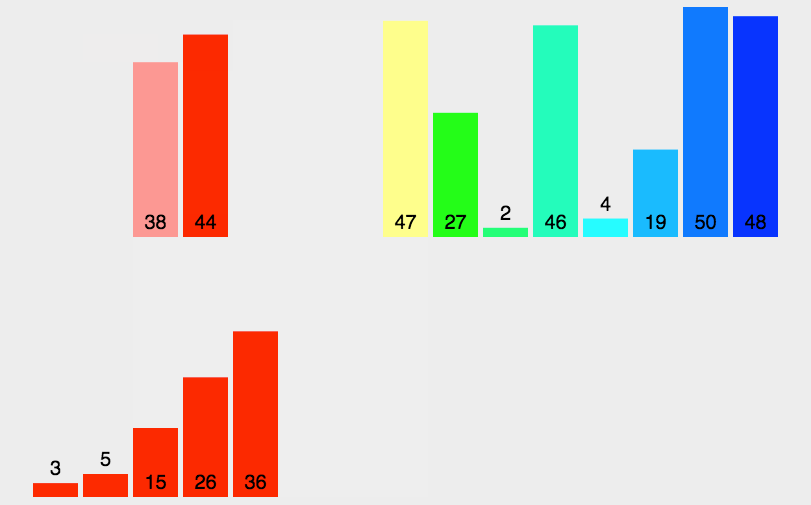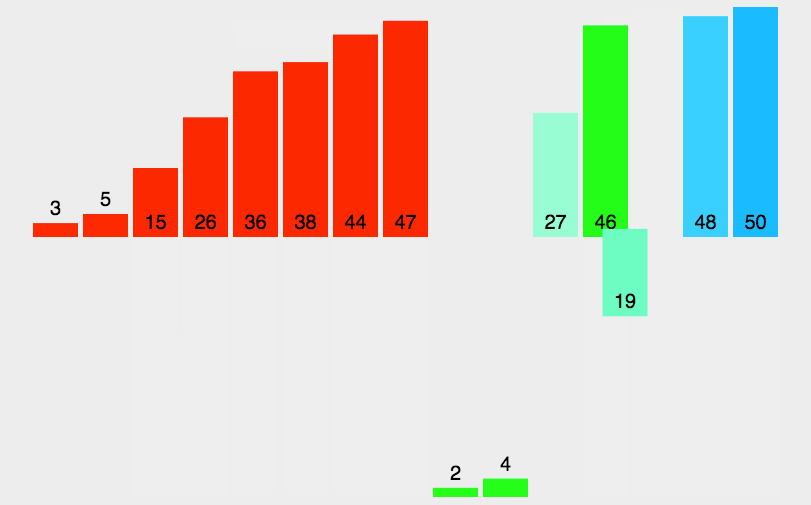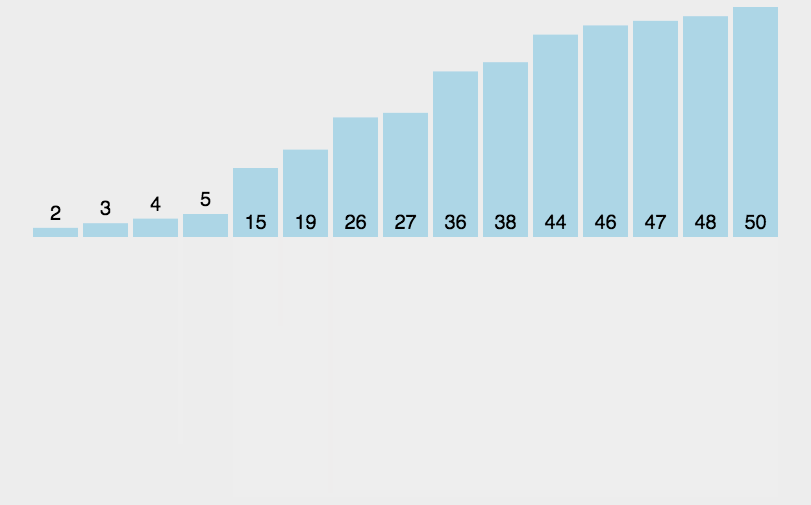
【排序】——七大排序算法详解

一、排序算法总览 

二、算法详解 

1、冒泡排序（Bubble Sort）

原理：比较两个相邻的元素，将值大的元素交换至右端。

思路：依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。重复第一趟步骤，直至全部排序完成。

public static void BubbleSort (int[] arr) {
　　　　for(int i=0;iarr[j+1]){
　　　　　　　　　　int temp=arr[j];
　　　　　　　　　　arr[j]=arr[j+1];
　　　　　　　　　　arr[j+1]=temp;
　　　　　　　　}
　　　　　　}
　　　　} 
　　}

2、选择排序（Selection Sort）

原理：每一趟从待排序的记录中选出最小的元素，顺序放在已排好序的序列最后，直到全部记录排序完毕。也就是：每一趟在n-i+1(i=1，2，…n-1)个记录中选取关键字最小的记录作为有序序列中第i个记录。基于此思想的算法主要有简单选择排序、树型选择排序和堆排序。（这里只介绍常用的简单选择排序）

思路：给定数组：int[] arr={里面n个数据}；第1趟排序，在待排序数据arr[1]~arr[n]中选出最小的数据，将它与arrr[1]交换；第2趟，在待排序数据arr[2]~arr[n]中选出最小的数据，将它与r[2]交换；以此类推，第i趟在待排序数据arr[i]~arr[n]中选出最小的数据，将它与r[i]交换，直到全部排序完成。

public static void SelectionSort(int[] arr) {       
        //选择排序的优化
        for(int i = 0; i < arr.length - 1; i++) {// 做第i趟排序
            int k = i;
            for(int j = k + 1; j < arr.length; j++){// 选最小的记录
                if(arr[j] < arr[k]){ 
                    k = j; //记下目前找到的最小值所在的位置
                }
            }
            //在内层循环结束，也就是找到本轮循环的最小的数以后，再进行交换
            if(i != k){  //交换a[i]和a[k]
                int temp = arr[i];
                arr[i] = arr[k];
                arr[k] = temp;
            }    
        }
    }

3、插入排序（Insertion Sort）

原理：通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。 

思路：在一个已经有序的小序列的基础上，一次插入一个元素。当然，刚开始这个有序的小序列只有1个元素，就是第一个元素。比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比起，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么插入元素把想插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序，所以插入排序是稳定的。

public static void insertionSort(int[] a) {
        int tmp;
        for (int i = 1; i < a.length; i++) {
            for (int j = i; j > 0; j--) {
                if (a[j] < a[j - 1]) {
                    tmp = a[j - 1];
                    a[j - 1] = a[j];
                    a[j] = tmp;
                }
            }
        }
}

 4、希尔排序（Shell Sort）

原理：把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。 

思路：对于n个待排序的数列，取一个小于n的整数gap(gap被称为步长)将待排序元素分成若干个组子序列，所有距离为gap的倍数的记录放在同一个组中；然后，对各组内的元素进行直接插入排序。 这一趟排序完成之后，每一个组的元素都是有序的。然后减小gap的值，并重复执行上述的分组和排序。重复这样的操作，当gap=1时，整个数列就是有序的。

public static void shellSort(int[] arrays) { 
    //增量每次都/2 
    for (int step = arrays.length / 2; step > 0; step /= 2) { 
        //从增量那组开始进行插入排序，直至完毕 
        for (int i = step; i < arrays.length; i++) { 
            int j = i; int temp = arrays[j]; 
            // j - step 就是代表与它同组隔壁的元素 
            while (j - step >= 0 && arrays[j - step] > temp) {
                 arrays[j] = arrays[j - step]; 
                j = j - step; 
            } 
            arrays[j] = temp; 
        } 
    } 
}

 5、归并排序（Merge Sort）

原理：典型的基于分治的递归算法。它不断地将原数组分成大小相等的两个子数组(可能相差1)，最终当划分的子数组大小为1时，将划分的有序子数组合并成一个更大的有序数组

思路：一个是分，也就是把原数组划分成两个子数组的过程。另一个是治，它将两个有序数组合并成一个更大的有序数组。它将数组平均分成两部分: center = (left + right)/2，当数组分得足够小时---数组中只有一个元素时，只有一个元素的数组自然而然地就可以视为是有序的，此时就可以进行合并操作了。因此，上面讲的合并两个有序的子数组，是从 只有一个元素 的两个子数组开始合并的。

    public static void sort(int []arr){
        int []temp = new int[arr.length];//在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
        sort(arr,0,arr.length-1,temp);
    }
    private static void sort(int[] arr,int left,int right,int []temp){
        if(left

 6、快速排序（Quick Sort）

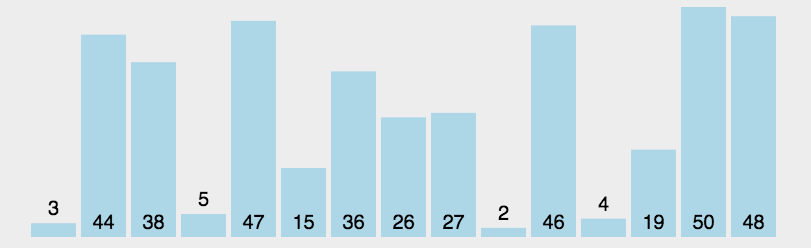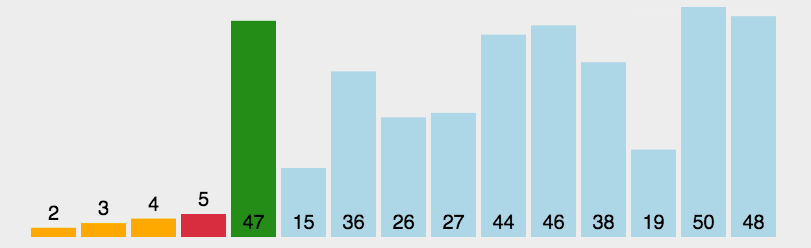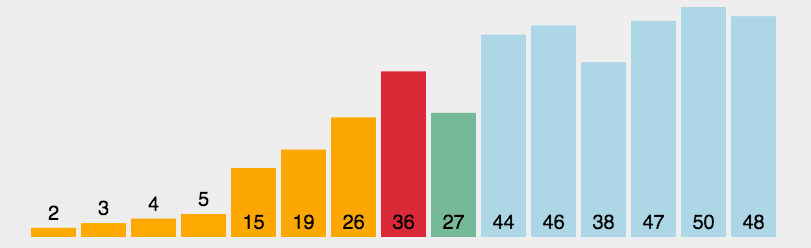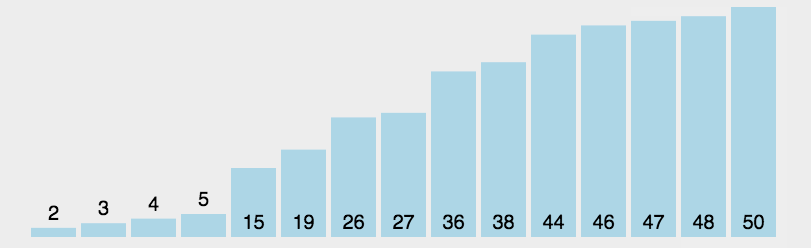
原理：选择一个关键值作为基准值。比基准值小的都在左边序列（一般是无序的），比基准值大的都在右边（一般是无序的）。一般选择序列的第一个元素。

思路：一次循环：从后往前比较，用基准值和最后一个值比较，如果比基准值小的交换位置，如果没有继续比较下一个，直到找到第一个比基准值小的值才交换。找到这个值之后，又从前往后开始比较，如果有比基准值大的，交换位置，如果没有继续比较下一个，直到找到第一个比基准值大的值才交换。直到从前往后的比较索引>从后往前比较的索引，结束第一次循环，此时，对于基准值来说，左右两边就是有序的了。

接着分别比较左右两边的序列，重复上述的循环。

public static void quickSort(int arr[],int _left,int _right){
        int left = _left;
        int right = _right;
        int temp = 0;
        if(left <= right){   //待排序的元素至少有两个的情况
            temp = arr[left];  //待排序的第一个元素作为基准元素
            while(left != right){   //从左右两边交替扫描，直到left = right

                while(right > left && arr[right] >= temp)  
                     right --;        //从右往左扫描，找到第一个比基准元素小的元素
                  arr[left] = arr[right];  //找到这种元素arr[right]后与arr[left]交换

                while(left < right && arr[left] <= temp)
                     left ++;         //从左往右扫描，找到第一个比基准元素大的元素
                  arr[right] = arr[left];  //找到这种元素arr[left]后，与arr[right]交换

            }
            arr[right] = temp;    //基准元素归位
            quickSort(arr,_left,left-1);  //对基准元素左边的元素进行递归排序
            quickSort(arr, right+1,_right);  //对基准元素右边的进行递归排序
        }        
    }

7、堆排序（Heap Sort）

原理：利用堆积树（堆）这种数据结构所设计的一种排序算法，它是选择排序的一种。可以利用数组的特点快速定位指定索引的元素

思路：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了

public static void sort(int[] arr) {
		//构建大顶堆
		for(int i=arr.length/2-1;i>=0;i--) {
			//调整堆结构，父节点大于左右子节点
			adjustHeap(arr,i,arr.length);
		}

		
		for(int j=arr.length-1;j>=0;j--) {
			swap(arr,0,j);                //调整大顶堆中根节点与末尾节点的位置
			adjustHeap(arr,0,j);     //重新调整为大顶堆
		}
	}
	pulic void adjustHeap(int[] arr,int i,int length) {
		int temp = arr[i];                //取出当前元素
		for(int k=2*i+1;ktemp) {          //如果子节点大于父节点，将子节点赋给父节点
				arr[i] = arr[k];
				i = k;
			} else {
				break;
			}
		}
		arr[i] = temp;       //将原父节点的值给子节点
	}
	//完成交换
	public void swap(int[] arr,int a,int b) {
		int temp = arr[a];
		arr[a] = arr[b];
		arr[b] = temp;
	}

三、算法性能分析

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
• 不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；
• 内排序：所有排序操作都在内存中完成；
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
• 时间复杂度： 一个算法执行所耗费的时间。
• 空间复杂度：运行完一个程序所需内存的大小。
• n: 数据规模
• k: “桶”的个数
• In-place: 占用常数内存，不占用额外内存
• Out-place: 占用额外内存