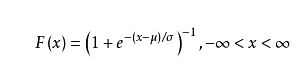十大机器学习算法笔记
基本概念分类
**监督式学习:**多轮学习以达到目的:实现回归或分类
**非监督式学习:**特定方法实现聚类。(由于目的性不明确,所以一般没有多轮)
**强化学习:**不断学习,永无止境
**分类算法:**适用因变量为离散变量
**回归算法:**适用因变量为连续变量
聚类和分类的差别:
**聚类:**无限种类别可能
**分类:**有限种类别可能
监督式学习
工作机制:
这个算法由一个目标变量或结果变量(或因变量)组成。
此变量由已知的一系列预示变量(自变量)预测而来。
利用这一系列变量,我们生成一个将输入值映射到期望输出值的函数。
这个训练过程会一直持续,直到模型在训练数据上获得期望的精确度。
例子:
线性回归,决策树,SVM,K – 近邻算法,逻辑回归 等
非监督式学习
工作机制:
没有任何目标变量或结果变量要预测或估计。
用在不同的组内聚类分析。
例子:
关联算法, K – 均值算法
强化学习
工作机制:
训练机器进行决策。
机器被放在一个能让它通过反复试错来训练自己的环境中。
机器从过去的经验中进行学习,并且尝试利用了解最透彻的知识作出精确的判断。
例子:
马尔可夫决策过程
十大机器学习算法
1、线性回归
2、逻辑回归
3、决策树
4、SVM
5、朴素贝叶斯
6、k-Means算法
7、kNN算法
8、Apriori算法
9、最大期望算法(EM)
10、PageRank**
监督式学习与非监督式学习的差别
监督式学习方法,要求:
事先明确知道各个类别的信息
所有待分类项都有一个类别与之对应
如果不能满足上述两个条件(例如有海量数据),则需适用聚类算法,即非监督式学习。

线性回归
适用场景
根据连续变量估计实际数值(房价、呼叫次数、总销售额等)。
原理
可通过拟合最佳直线来建立自变量和因变量的关系。拟合结果是条直线 Y= a *X + b:其中Y是因变量,a是斜率,x是自变量,b是截距,最佳直线叫做回归线。系数 a 和 b 通过最小二乘法获得。
from sklearn import linear_model
x_train=input_variables_values_training_datasets #输入的训练集特征变量
y_train=target_variables_values_training_datasets #输入的训练集目标变量
x_test=input_variables_values_test_datasets #输入的测试集特征变量
linear = linear_model.LinearRegression()
linear.fit(x_train, y_train)
linear.score(x_train, y_train)
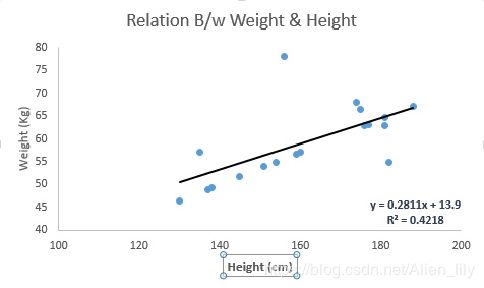
针对线性回归容易出现欠拟合的问题,采取局部加权线性回归。
在该算法中,赋予预测点附近每一个点以一定的权值,在这上面基于波长函数来进行普通的线性回归.可以实现对临近点的精确拟合同时忽略那些距离较远的点的贡献,即近点的权值大,远点的权值小,k为波长参数,控制了权值随距离下降的速度,越大下降的越快。
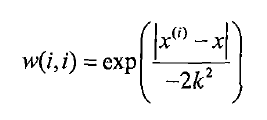
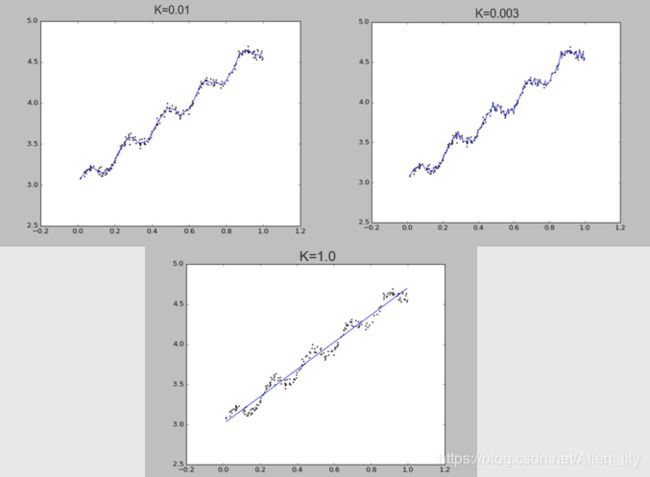
针对数据的特征比样本点多的问题:
一、岭回归
二、前向逐步回归
逻辑回归
适用场景
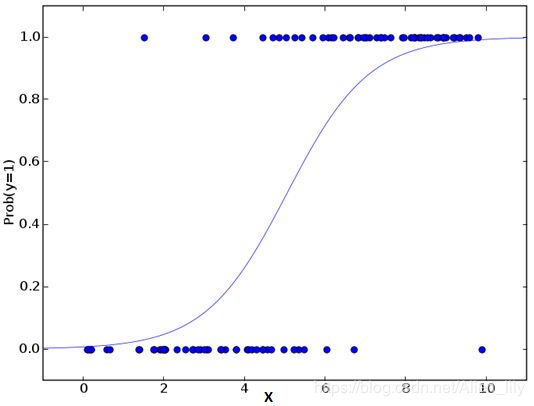
该算法可根据已知的一系列因变量估计离散数值的出现概率。
原理
这是一个分类算法而不是回归算法。
从数学上看,在结果中,几率的对数使用的是预测变量的线性组合模型。
ln(p/(1-p)) = b0 +b1x1+b2x2=b3x3+…+bkxk
分布函数
#Import Library
from sklearn.linear_model import LogisticRegression
#Assumed you have, X (predictor) and Y (target) for training data set and x_test(predictor) of test_dataset
# Create logistic regression object
model = LogisticRegression()
# Train the model using the training sets and check score
model.fit(X, y)
model.score(X, y)
#Predict Output
predicted= model.predict(x_test)
基于最优化方法的最佳回归系数确定:
梯度下降法------随机梯度下降法(根据梯度更新权重)
牛顿法或拟牛顿法(最大熵模型)
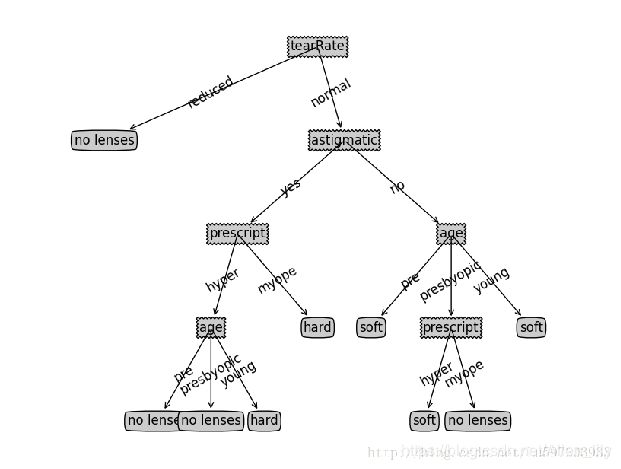
决策树
使用场景
这个监督式学习算法通常被用于分类问题。
它同时适用于分类变量和连续因变量。
原理
在这个算法中,我们将总体分成两个或更多的同类群。
这是根据最重要的属性或者自变量来分成尽可能不同的组别。
回归树——预测值为叶节点目标变量的加权均值
分类树——某叶节点预测的分类值应是造成错判损失最小的分类值。
细说决策树(1)——混乱度判断
熵
熵:E = sum(-p(I)*log(p(I))),I=1:N(N类结果,如客户是否流失)
所有样本都属于一个类别I(最整齐),那么熵为0,如果样本完全随机,那么熵为1
信息增益
信息增益:原样本的熵-sum(区分后的各部分熵),增益越大表示区分的方法越好
Gain(Sample,Action) = E(sample) - sum(|Sample(v)|/Sample * E(Sample(v)))
除了熵以外,还有GINI不纯度,错误率两种计算混乱度的方法,定义不同但效果类似。
细说决策树(2)——建构树
生成树
(1) 从根节点t=1开始,从所有可能候选S集合中搜索使不纯性降低最大的划分S;
(2)使用划分S将节点1(t=1)划分成两个节点t=2和t=3;
(3)在t=2和t=3上分别重复划分搜索过程
终止树
(1)节点达到完全纯性;
(2)树的深度达到用户指定的深度;
(3)节点中样本的个数少于用户指定的个数;
(4) 异质性指标下降的最大幅度小于用户指定的幅度。
细说决策树(3)——剪枝prune
当分类回归树划分得太细时,会对噪声数据产生过拟合作用。因此我们要通过剪枝来解决。剪枝又分为前剪枝和后剪枝:
前剪枝:在构造树的过程中就知道那些节点需要减掉,及早的停止树增长。
后剪枝:在构造出完整树之后再按照一定方法进行剪枝,方法有:代价复杂性剪枝、最小误差剪枝、悲观误差剪枝等等。
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet]#将最后一行的数据放到classList中
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:#这里为什么是1呢?就是说特征数为1的时候
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
print(bestFeat)
bestFeatLabel = labels[bestFeat]#运行结果'no surfacing'
myTree = {bestFeatLabel:{}}#运行结果{'no surfacing': {}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]#第0个特征值
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet\
(dataSet,bestFeat,value),subLabels)
return myTree
支持向量机
适用场景
这是一种统计分类及回归分析方法
算法
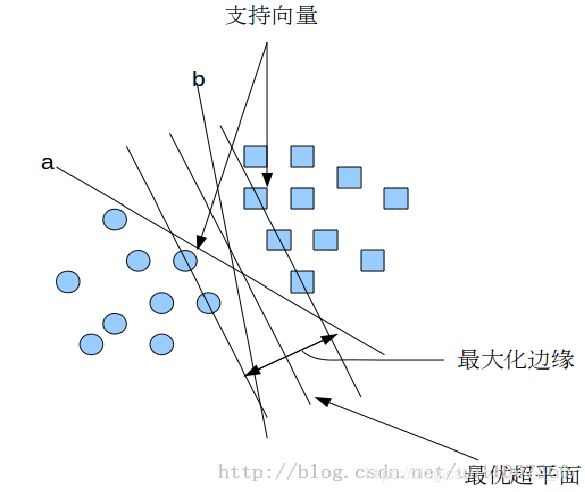
支持向量机将向量映射到一个更高维的空间里,
在这个空间里建立有一个最大间隔超平面。
在分开数据的超平面的两边建有两个互相平行的超平面,
分隔超平面使两个平行超平面的距离最大化。
假定平行超平面间的距离或差距越大,
分类器的总误差越小。
未完待续……